
Wetenschap
Een schaalbare deep learning-aanpak voor enorme grafieken

Figuur 1:Uitbreiding van de buurten vanaf de bruine knoop in het midden. Eerste uitbreiding:groen; tweede:geel; derde:rood.
Een grafiekstructuur is uiterst nuttig voor het voorspellen van eigenschappen van zijn bestanddelen. De meest succesvolle manier om deze voorspelling uit te voeren, is door elke entiteit aan een vector toe te wijzen door middel van diepe neurale netwerken. Men kan de gelijkenis van twee entiteiten afleiden op basis van de vectornabijheid. Een uitdaging voor diep leren, echter, is dat men informatie moet verzamelen tussen een entiteit en zijn uitgebreide omgeving over lagen van het neurale netwerk. De buurt breidt zich snel uit, rekenwerk erg kostbaar maken. Om deze uitdaging op te lossen, we stellen een nieuwe aanpak voor, gevalideerd door middel van wiskundige bewijzen en experimentele resultaten, die suggereren dat het voldoende is om de informatie van slechts een handvol willekeurige entiteiten in elke buurtuitbreiding te verzamelen. Deze substantiële reductie in buurtomvang geeft dezelfde kwaliteit van voorspelling als state-of-the-art diepe neurale netwerken, maar verlaagt de trainingskosten met orden van grootte (bijv. 10x tot 100x minder reken- en resourcetijd), wat leidt tot aantrekkelijke schaalbaarheid. Ons artikel waarin dit werk wordt beschreven, "FastGCN:snel leren met Graph Convolutional Networks via Importance Sampling, " zal worden gepresenteerd op ICLR 2018. Mijn co-auteurs zijn Tengfei Ma en Cao Xiao.
Complexiteit van grafiekanalyse
Grafieken zijn universele representaties van een paarsgewijze relatie. In toepassingen in de echte wereld, ze komen in verschillende vormen, waaronder bijvoorbeeld sociale netwerken, genexpressienetwerken, en kennisgrafieken. Een trending onderwerp in deep learning is om het opmerkelijke succes van gevestigde neurale netwerkarchitecturen voor Euclidische gestructureerde gegevens (zoals afbeeldingen en teksten) uit te breiden naar onregelmatig gestructureerde gegevens, inclusief grafieken. De grafiek convolutionele netwerk, GCN, is zo'n uitstekend voorbeeld. Het generaliseert het concept van convolutie voor afbeeldingen, die kan worden beschouwd als een raster van pixels, naar grafieken die er niet langer uitzien als een gewoon raster.
Het idee achter GCN is heel eenvoudig. Degenen onder ons die Signaalverwerking 101 of een basiscursus computervisie hebben gevolgd, zijn al bekend met het concept van een convolutiefilter. Voor afbeeldingen, het is een kleine matrix van getallen, elementsgewijs te vermenigvuldigen met een bewegend venster van het beeld, waarbij de resulterende productsom het middelste nummer van het venster vervangt. Voor grafieken, dit is vergelijkbaar. Een goede combinatie van de filters kan primitieve lokale structuren detecteren, zoals lijnen in verschillende hoeken, randen, hoeken, en vlekken van een bepaalde kleur. Voor grafieken, windingen zijn vergelijkbaar. Stel je voor dat elke grafiekknoop aanvankelijk is verbonden met een vector. Voor elk knooppunt, de vectoren van de buren worden erin opgeteld (met bepaalde gewichten en transformaties). Vandaar, alle knooppunten worden tegelijkertijd bijgewerkt, het uitvoeren van een laag van voorwaartse voortplanting. Grafiekconvoluties kunnen worden gebruikt om informatie door buurten te verspreiden, zodat globale informatie naar elk grafiekknooppunt wordt verspreid.
Het probleem van GCN is dat voor een netwerk met meerdere lagen, de buurt wordt snel uitgebreid, waarbij veel vectoren bij elkaar moeten worden opgeteld, voor zelfs maar één enkel knooppunt. Een dergelijke berekening is onbetaalbaar voor grafieken met een groot aantal knopen. Hoe groot zal een uitgebreide buurt eruit zien? In sociale netwerkanalyse, er is een beroemd concept bedacht "zes graden van scheiding, " waarin staat dat men elke andere persoon op aarde kan bereiken via zes tussenliggende verbindingen! Figuur 1 illustreert dat vanaf de bruine knoop in het midden, de buurt drie keer uitbreiden (in de volgorde van groen, geel, en rood) raakt bijna de hele grafiek. Met andere woorden, alleen de vector van de bruine knoop bijwerken is lastig voor een GCN met slechts drie lagen.
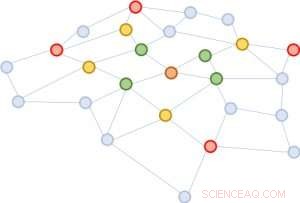
Figuur 2:Uitgaande van dezelfde bruine knoop, in elke wijkuitbreiding, we nemen slechts vier knooppunten als voorbeeld.
Vereenvoudiging voor schaalbaarheid
We stellen een eenvoudige maar krachtige oplossing voor, genaamd FastGCN. Als volledige uitbreiding van de wijk kostbaar is, waarom niet elke keer uitbreiden met slechts een paar buren? Figuur 2 illustreert het concept. Vanaf de bruine knoop, in elke uitbreiding kiezen we een constant aantal (vier) knooppunten en tellen alleen daarvan de vectoren op. De bemonstering vermindert de kosten voor het trainen van het neurale netwerk aanzienlijk, door de trainingstijd met orden van grootte te verminderen op benchmarkgegevenssets die vaak door onderzoekers worden gebruikt. Nog, voorspellingen blijven vergelijkbaar nauwkeurig. De grootte van deze benchmarkgrafieken varieert van een paar duizend knooppunten tot een paar honderdduizend knooppunten, bevestiging van de schaalbaarheid van onze methode.
Achter deze intuïtieve benadering schuilt een wiskundige theorie voor de benadering van de verliesfunctie. Een laag van het netwerk kan worden samengevat als een matrixvermenigvuldiging:H'=s(AHW), waarbij A de aangrenzende matrix van de grafiek is, elke rij van H is de vector die aan de knooppunten is bevestigd, W is een lineaire transformatie van de vectoren (ook geïnterpreteerd als de te leren modelparameter), en de rijen van H' bevatten de bijgewerkte vectoren. We generaliseren deze matrixvermenigvuldiging naar een integrale transformatie h'(v)=s(òA(v, u)h(u)W dP(u)) onder een waarschijnlijkheidsmaat P. Dan, de bemonstering van een vast aantal buren in elke uitbreiding is niets anders dan een Monte Carlo-benadering van de integraal onder de maat P. De Monte Carlo-benadering levert een consistente schatter van de verliesfunctie op; Vandaar, door de helling te nemen, we kunnen een standaard optimalisatiemethode (zoals stochastische gradiëntafdaling) gebruiken om het neurale netwerk te trainen.
Een scala aan deep learning-toepassingen
Onze aanpak pakt een belangrijke uitdaging aan op het gebied van deep learning voor grootschalige grafieken. Het is niet alleen van toepassing op GCN, maar ook op vele andere neurale netwerken die gebaseerd zijn op het concept van buurtuitbreiding, een essentieel onderdeel van het leren van grafiekrepresentatie. We voorzien dat de oplossing van de uitdaging in deze fundamentele gegevensstructuur - grafieken - zal worden toegepast in een breed scala aan toepassingen, inclusief de analyse van sociale netwerken, het diepe inzicht in eiwit-eiwit interacties voor het ontdekken van geneesmiddelen, en het samenstellen en ontdekken van informatie in kennisbanken.
 SARS-CoV-2 in vaste stoffen in afvalwater kan de verspreiding van COVID-19 helpen monitoren
SARS-CoV-2 in vaste stoffen in afvalwater kan de verspreiding van COVID-19 helpen monitoren Onderzoek effent de weg voor de volgende generatie kristallijne materiaalzeefapparatuur
Onderzoek effent de weg voor de volgende generatie kristallijne materiaalzeefapparatuur Biologisch geïnspireerd, hoogwaardig polyurethaan ontwikkeld voor rekbare elektronica
Biologisch geïnspireerd, hoogwaardig polyurethaan ontwikkeld voor rekbare elektronica Hoe het volume van CO2-gas in vloeistof om te zetten
Hoe het volume van CO2-gas in vloeistof om te zetten  Engineering ECM-achtige vezels met bioactieve zijde voor 3D-celkweek
Engineering ECM-achtige vezels met bioactieve zijde voor 3D-celkweek
 Lijst met dieren die in zwart-wit zien
Lijst met dieren die in zwart-wit zien  Microbe kauwt door PFAS en andere taaie verontreinigingen
Microbe kauwt door PFAS en andere taaie verontreinigingen Geologen gebruiken paleomagnetisme om de reeks gebeurtenissen te bepalen die resulteerden in het Himalaya-gebergte
Geologen gebruiken paleomagnetisme om de reeks gebeurtenissen te bepalen die resulteerden in het Himalaya-gebergte Nieuwe tool om de bouwsector te helpen de ecologische voetafdruk te verkleinen
Nieuwe tool om de bouwsector te helpen de ecologische voetafdruk te verkleinen Hoe we plastic afval kunnen omzetten in groene energie
Hoe we plastic afval kunnen omzetten in groene energie
Hoofdlijnen
- Hogere biodiversiteit door rivierverruimende maatregelen
- Wat zijn enkele voor- en nadelen van het gebruik van DNA-analyse om rechtshandhaving bij criminaliteit te bevorderen?
- Verbazingwekkende diversiteit aan soorten gerapporteerd over Solent oesterrestauratieproject
- De effecten van algen in drinkwater
- Dahls paddenkopschildpad bedreigd door versnipperd leefgebied, krimpende bevolking
- Klimaatverandering maakt baardagamen mogelijk minder intelligent
- Onderbroken herprogrammering zet volwassen cellen om in hoge opbrengsten van voorloperachtige cellen
- Kan slapen met een hersenschudding je doden?
- Disruptieve bio-engineering - verandert de manier waarop cellen met elkaar omgaan
- Sommige apps voor mobiele telefoons kunnen verborgen gedrag bevatten dat gebruikers nooit zien

- Geavanceerde biobrandstoffen kunnen uiterst efficiënt worden geproduceerd

- 3D-afbeeldingen maken met gewone inkt

- Hoogwaardige componenten gemaakt door galvaniseren

- VS voert druk op Europa op vanwege 5G-infrastructuur van China's Huawei

 Onderzoekers boren diep om te begrijpen waarom de aardbeving op Sumatra zo hevig was
Onderzoekers boren diep om te begrijpen waarom de aardbeving op Sumatra zo hevig was Effectiviteit van stoffen maskers hangt af van het type bekleding
Effectiviteit van stoffen maskers hangt af van het type bekleding Nucleatie een zegen voor duurzame nanofabricage
Nucleatie een zegen voor duurzame nanofabricage Groene aanpak versnelt procesoptimalisatie en terugwinning van schakelbare oplosmiddelen
Groene aanpak versnelt procesoptimalisatie en terugwinning van schakelbare oplosmiddelen De zoektocht naar leven op Mars breidt zich uit naar het bestuderen van zijn manen
De zoektocht naar leven op Mars breidt zich uit naar het bestuderen van zijn manen Nieuwe techniek maakt de weg vrij voor perfecte perovskieten
Nieuwe techniek maakt de weg vrij voor perfecte perovskieten Het testen van chimpansees in Tanzania gedurende tientallen jaren suggereert dat persoonlijkheidstypes stabiel zijn
Het testen van chimpansees in Tanzania gedurende tientallen jaren suggereert dat persoonlijkheidstypes stabiel zijn Apple Watch ECG-functie om onregelmatige hartslag te detecteren:ik heb het geprobeerd
Apple Watch ECG-functie om onregelmatige hartslag te detecteren:ik heb het geprobeerd
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Portuguese | Swedish | German | Dutch | Danish | Norway | Spanish |

-
Wetenschap © https://nl.scienceaq.com

