
Wetenschap
Wat zijn de methoden voor formuletransformatie?
Het optellen of aftrekken van een constante aan elke kant van een vergelijking zal de gelijkheid niet veranderen.
Bijvoorbeeld voor de vergelijking
$$x+2=5,$$
we kunnen er 3 aan beide kanten optellen om te krijgen
$$x+2+3=5+3,$$
wat vereenvoudigt
$$x+5=8$$
We kunnen ook van beide kanten 2 aftrekken om te krijgen
$$x+2-2=5-2,$$
wat vereenvoudigt
$$x=3.$$
2. Vermenigvuldigen of delen
Het vermenigvuldigen of delen van beide zijden van een vergelijking door een constante die niet nul is, zal de gelijkheid niet veranderen.
Bijvoorbeeld voor de vergelijking
$$3x=15,$$
we kunnen beide zijden door 3 delen om te krijgen
$$\frac{3x}{3}=\frac{15}{3},$$
wat vereenvoudigt
$$x=5.$$
We kunnen ook beide zijden met 2 vermenigvuldigen om te krijgen
$$3x\cdot2=15\cdot2,$$
wat vereenvoudigt
$$6x=30$$
3. Factoring
Factoring is een proces waarbij een uitdrukking wordt geschreven als een product van eenvoudigere uitdrukkingen.
Bijvoorbeeld voor de vergelijking
$$x^2+2x-3=0,$$
we kunnen als volgt factoriseren:
$$(x+3)(x-1)=0$$
Als we elke factor gelijk stellen aan nul, krijgen we
$$x+3=0 \quad \text{of} \quad x-1=0$$
Als we elke vergelijking oplossen, krijgen we
$$x=-3 \quad \text{of} \quad x=1$$
4. Het vierkant voltooien
Het voltooien van het vierkant is een proces waarbij een kwadratische vergelijking wordt omgezet in een perfect vierkant.
Bijvoorbeeld voor de vergelijking
$$x^2-4x-5=0,$$
we kunnen het vierkant als volgt voltooien:
$$x^2-4x+4-4-5=0$$
$$(x-2)^2-9=0$$
Als we aan beide kanten 9 optellen, krijgen we
$$(x-2)^2=9$$
Als we de wortel van beide kanten nemen, krijgen we:
$$x-2=\pm3$$
Als we elke vergelijking oplossen, krijgen we
$$x=2+3=5 \quad \text{of} \quad x=2-3=-1$$
5. Vervanging
Vervanging is een proces waarbij één uitdrukking wordt vervangen door een andere gelijkwaardige uitdrukking.
Bijvoorbeeld voor de vergelijking
$$y=3x+2$$
we kunnen \(y\) vervangen door \(x+5\):
$$x+5=3x+2$$
Oplossen voor \(x\):
$$x-3x=-5+2$$
$$-2x=-3$$
$$x=\frac{3}{2}$$
 Een nieuwe benadering voor dimensionale engineering van covalente organische raamwerken afgeleide koolstofatomen
Een nieuwe benadering voor dimensionale engineering van covalente organische raamwerken afgeleide koolstofatomen  Hoe calciumchloride en water te mengen
Hoe calciumchloride en water te mengen Een stap vooruit in farmaceutisch onderzoek
Een stap vooruit in farmaceutisch onderzoek Usurpeert de boer:hoe zeewier kan helpen het boeren van koeien (en hun uitstoot) te beteugelen
Usurpeert de boer:hoe zeewier kan helpen het boeren van koeien (en hun uitstoot) te beteugelen  Nieuwe beeldvormingstechniek onthult hoe mechanische schade begint op moleculaire schaal
Nieuwe beeldvormingstechniek onthult hoe mechanische schade begint op moleculaire schaal
 Nieuwe kaart onthult verloren habitat in estuarium aan de westkust
Nieuwe kaart onthult verloren habitat in estuarium aan de westkust Hoe groene bestrating werkt
Hoe groene bestrating werkt Zaadmengsels en verzekeringsongediertebestrijding:toekomstige norm in de Corn Belt?
Zaadmengsels en verzekeringsongediertebestrijding:toekomstige norm in de Corn Belt?  Is het uitroepen van een klimaatnoodtoestand voldoende om de klimaatcrisis te stoppen? Wat we kunnen leren van de COVID-19-pandemie
Is het uitroepen van een klimaatnoodtoestand voldoende om de klimaatcrisis te stoppen? Wat we kunnen leren van de COVID-19-pandemie Wat is het verschil tussen hagedissen en gekko's?
Wat is het verschil tussen hagedissen en gekko's?
Hoofdlijnen
- Uitbreiding tonijnquota stap achteruit voor instandhouding
- Wat doet boor in het menselijk lichaam?
- Welke koninkrijken zijn heterotroof en autotroof?
- Hoe de neus van een baby de geur van mama kent
- Video:Waarom hebben we nog geen synthetisch bloed?
- De biodiversiteit van de aarde verandert naarmate de planeet opwarmt. Maar hoe?
- Waar vindt glucoserosorbtie plaats?
- Alle in Michigan bevestigde poema's waren mannelijk:waarom we geen vrouwtjes en kittens zien
- Wat zijn de vijf belangrijkste functies van het skeletsysteem?
- Het degradatiegedrag van geavanceerde medische apparaten voorspellen

- De toekomst van zuivering verbeteren door moleculair silhouet te gebruiken om verbindingen in vloeistoffen te scheiden

- Vervaardiging van aluminiumlegeringen nu 50% energiezuiniger

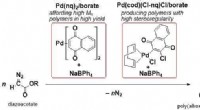
- Nieuwe op palladium gebaseerde initiatiesystemen voor C1-polymerisatie van diazoacetaten
- Het molecuul begrijpen en beheersen dat het universum heeft gemaakt

 Hoe Comcast het kabelspel probeert te veranderen
Hoe Comcast het kabelspel probeert te veranderen  Schoolprojecten op de Melkweg Galaxy
Schoolprojecten op de Melkweg Galaxy Wat is goed aan de moesson?
Wat is goed aan de moesson?  Wat is de beweging van gesteente door wind en waterzwaartekracht?
Wat is de beweging van gesteente door wind en waterzwaartekracht?  Ideale huwelijkspartners drijven Waorani-krijgers naar de oorlog
Ideale huwelijkspartners drijven Waorani-krijgers naar de oorlog Is water een alkali in de chemie?
Is water een alkali in de chemie?  Nanogestructureerde sensoren voeden nieuw kankerdetectiesysteem
Nanogestructureerde sensoren voeden nieuw kankerdetectiesysteem Ruimtevaartuig zoemt Jupiters megamaan, 1e close-up in jaren
Ruimtevaartuig zoemt Jupiters megamaan, 1e close-up in jaren
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

