
Wetenschap
Perovskieten tellen

Glazen buizen met quantum dots van perovskiet nanokristallen, oplichtend met alle kleuren van de regenboog onder ultraviolette straling. Krediet:Shutterstock
Marina Filip, Postdoctoraal onderzoeksassistent, en Feliciano Giustino, Hoogleraar materialen, zowel bij de afdeling Materialen, uitleggen hoe elementaire geometrie en moderne data-analyse kunnen worden gecombineerd om het bestaan van duizenden nieuwe materialen, 'perovskieten' genaamd, te voorspellen, zoals blijkt uit hun recente publicatie in PNAS .
Perovskieten zijn een brede familie van kristallen die dezelfde structurele rangschikking delen als het mineraal CaTiO3. De buitengewone aantrekkingskracht van perovskieten is hun ongewone chemische veelzijdigheid, omdat ze over het algemeen bijna elk element in het periodiek systeem kunnen opnemen. Dit leidt tot een ongelooflijk divers scala aan functionaliteiten. Bijvoorbeeld, twee belangrijke wetenschappelijke ontdekkingen van onze tijd zijn prominent aanwezig in perovskieten, hoge temperatuur supergeleiding in perovskiet cupraten (Bednorz en Müller, Nobelprijs 1987) en de recente ontdekking van de perovskiet-zonnecellen (Snaith, Universiteit van Oxford 2012).
In onze eigen studie wilden we begrijpen waarom bepaalde combinaties van elementen in het periodiek systeem als perovskietkristallen worden gerangschikt en andere niet, en of we konden anticiperen hoeveel en welke perovskieten er nog ontdekt moeten worden.
Het bleek dat de Noorse mineraloog Victor Goldschmidt in 1926 precies dezelfde vraag stelde. Op basis van empirische waarnemingen, hij stelde voor dat de vormbaarheid van perovskieten een eenvoudig geometrisch principe volgt, namelijk:Het aantal anionen dat een kation omringt is meestal zo groot mogelijk, op voorwaarde dat alle anionen het kation raken. Deze verklaring staat bekend als de 'niet-ratelen'-hypothese, en betekent in wezen dat als we een kristal beschrijven met behulp van een model van stijve bollen, in een perovskiet zijn de bollen vaak dicht op elkaar gepakt, zodat niemand zich vrij kan bewegen. Met behulp van elementaire meetkunde kan de hypothese van Goldschmidt worden vertaald in een reeks van zes eenvoudige wiskundige regels waaraan de ionen van een perovskiet moeten voldoen.
De hypothese van Goldschmidt is de afgelopen eeuw in een of andere vorm in talloze onderzoeken gebruikt, om de vorming van perovskieten in kwalitatieve termen te verklaren, maar de voorspellende kracht ervan was nooit kwantitatief beoordeeld. We realiseerden ons dat, in tegenstelling tot 1926, in 2018 profiteren we van een eeuw onderzoek in kristallografie, gedocumenteerd in openbaar beschikbare databases van kristalstructuren, zoals de anorganische kristalstructuurdatabase, en meer dan 50, 000 gepubliceerde wetenschappelijke artikelen over perovskietverbindingen. Met behulp van internetdatamining en statistische analyse, we waren in staat om een bibliotheek van meer dan 2000 chemische verbindingen te verzamelen en te bestuderen waarvan bekend is dat ze zich in verschillende kristalstructuren vormen, en gebruik ze om de voorspellende kracht van de hypothese van Goldschmidt te testen. We ontdekten dat dit zeer elegante geometrische model in staat is onderscheid te maken tussen verbindingen die perovskieten zijn en verbindingen die geen hoger succespercentage hebben dan geavanceerde kwantummechanische benaderingen.
In onze studie gebruikten we dit eenvoudige model om bijna vier miljoen composities te screenen, en voorspellen het bestaan van meer dan 90, 000 nieuwe perovskietmaterialen die nog niet zijn gesynthetiseerd. Deze bibliotheek van voorspelde verbindingen biedt de opwindende uitdaging om de functionaliteiten van deze nieuwe perovskieten te ontdekken voor de gemeenschap die werkt aan de synthese en karakterisering van nieuwe materialen. Het belangrijkste is, onze ontdekking kan leiden tot de realisatie van geheel nieuwe functionele materialen voor een breed scala aan technologieën, van toepassingen in energie, elektronica en medicijnen.
 We composteerden biologisch afbreekbare ballonnen. Dit is wat we vonden na 16 weken
We composteerden biologisch afbreekbare ballonnen. Dit is wat we vonden na 16 weken Wetenschappers vinden zelfherstellende katalysator voor mogelijk grootschalig gebruik bij waterstofproductie
Wetenschappers vinden zelfherstellende katalysator voor mogelijk grootschalig gebruik bij waterstofproductie Een metallopeptide richt zich op en verstoort de mitochondriale functie in stamcellen van borstkanker
Een metallopeptide richt zich op en verstoort de mitochondriale functie in stamcellen van borstkanker Snel, nauwkeurige manier om pindaplanten te controleren op gezonde eigenschappen
Snel, nauwkeurige manier om pindaplanten te controleren op gezonde eigenschappen Hoe oplosbaarheid te bepalen Percentage
Hoe oplosbaarheid te bepalen Percentage
 Wegenzout kan ecosystemen in gevaar brengen, watervoorziening
Wegenzout kan ecosystemen in gevaar brengen, watervoorziening Coronavirus:hebben we de kans om een betere wereld te bouwen al gemist?
Coronavirus:hebben we de kans om een betere wereld te bouwen al gemist? Wetenschappers:risico op explosieve uitbarsting stijgt voor vulkaan Hawaï
Wetenschappers:risico op explosieve uitbarsting stijgt voor vulkaan Hawaï NASA vindt Herold een vervagende ex-tropische cycloon
NASA vindt Herold een vervagende ex-tropische cycloon Onderzoekers beweren dat inspanningen voor waterirrigatie-efficiëntie in feite leiden tot meer watergebruik
Onderzoekers beweren dat inspanningen voor waterirrigatie-efficiëntie in feite leiden tot meer watergebruik
Hoofdlijnen
- Daar is een studie over:het stenen tijdperk had net zoveel linkse mensen
- Lijst met genotypes
- Anatomie en fysiologie van een synapsenstructuur
- Lignine-afval aangepast voor industrieel gebruik van bio-olie
- Waarom stak de olifant de weg over? In Maleisië, ze proberen het antwoord te vinden
- Aminozuren: functie, structuur, typen
- Schoonmaken van microscoopglaasjes
- Het is onwaarschijnlijk dat de jacht op trofeeën de evolutie beïnvloedt
- Temperatuur kan de pollenkleur beïnvloeden
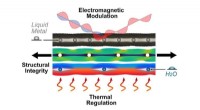
- Bio-geïnspireerde microvasculatuur gebruiken om materiaaleigenschappen te beheersen
- Chili-vormig apparaat zou kunnen onthullen hoe heet die peper is
- Blauwe kleurstof uit rode bieten:scheikundigen bedenken een nieuwe pigmentoptie

- Efficiëntere fotokatalysatoren kunnen het potentieel van zonne-energie ontsluiten

- Wat zijn de 4 atoommodellen?
 Google geeft $ 25 miljoen weg om humane AI-projecten te financieren
Google geeft $ 25 miljoen weg om humane AI-projecten te financieren Help ons erachter te komen hoe onze mogelijk bewoonbare buur van de exoplaneet er in werkelijkheid uitziet
Help ons erachter te komen hoe onze mogelijk bewoonbare buur van de exoplaneet er in werkelijkheid uitziet Hoe 180 graden metrisch in Fahrenheit te converteren
Hoe 180 graden metrisch in Fahrenheit te converteren  Virgin Atlantic kan folden zonder hulp van de staat:Branson
Virgin Atlantic kan folden zonder hulp van de staat:Branson CES Gadget Show:Surveillance is in - en op een grote manier
CES Gadget Show:Surveillance is in - en op een grote manier Een nieuw type chemische microscopie met superresolutie
Een nieuw type chemische microscopie met superresolutie Afleveringssystemen voor deeltjesvormige vaccins kunnen helpen beschermen tegen uitbraken van infectieziekten en bioterreurbedreigingen
Afleveringssystemen voor deeltjesvormige vaccins kunnen helpen beschermen tegen uitbraken van infectieziekten en bioterreurbedreigingen Geen grafeen:onderzoekers ontdekken nieuw type atomair dun koolstofmateriaal
Geen grafeen:onderzoekers ontdekken nieuw type atomair dun koolstofmateriaal
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

