
Wetenschap
Een slinger heeft op aarde een periode van 1,35 s. Wat is de oppervlaktemaan waarbij g gelijk is aan 1,62 meter per seconde in het kwadraat?
$$T =2\pi\sqrt{\frac{L}{g}}$$
Waar T de periode van de slinger in seconden is, is L de lengte van de slinger in meters, en g de versnelling als gevolg van de zwaartekracht in meters per secondekwadraat.
Omdat de lengte van de slinger op aarde en op de maan hetzelfde is, kunnen we de periode op aarde gebruiken om de lengte van de slinger te vinden:
$$L =\frac{T^2g}{4\pi^2}$$
Als we de gegeven waarden vervangen, krijgen we:
$$L =\frac{(1,35 \text{ s})^2 (9,8 \text{ m/s}^2)}{4\pi^2} =1,43 \text{ m}$$
Nu kunnen we de bovenstaande formule gebruiken om de periode op de maan te vinden:
$$T =2\pi\sqrt{\frac{L}{g}} =2\pi\sqrt{\frac{1,43 \text{ m}}{1,62 \text{ m/s}^2}} =2,73 \tekst{ s}$$
Daarom is de periode van de slinger op het oppervlak van de maan 2,73 seconden.
 Gefossiliseerde algen zijn veelbelovend voor verbeterde voedselveiligheidstesten
Gefossiliseerde algen zijn veelbelovend voor verbeterde voedselveiligheidstesten Virulentiefactor van het influenza A-virus in realtime in kaart gebracht
Virulentiefactor van het influenza A-virus in realtime in kaart gebracht Wat is watervrije diethylether?
Wat is watervrije diethylether?  Gips dat in de mond blijft plakken, kan de behandeling van orale aandoeningen verbeteren
Gips dat in de mond blijft plakken, kan de behandeling van orale aandoeningen verbeteren Wetenschappers onthullen verborgen katalytisch oppervlak van Ni-Au-kernschil in kooldioxidehydrogenering
Wetenschappers onthullen verborgen katalytisch oppervlak van Ni-Au-kernschil in kooldioxidehydrogenering
Hoofdlijnen
- Wat is de langste tijd dat iemand zonder slaap is geweest?
- Waarom hopen wetenschappers een manier te ontdekken om de rijping te versnellen?
- Hoe te studeren voor menselijke biologie examens
- Nieuw onderzoek onthult hoe vleermuishersenen zijn georganiseerd voor echolocatie en vlucht
- Waarom zijn er minder organismen op de hogere trofische niveaus dan op de lagere niveaus?
- DNA uit fossiele eierschalen onthult hoe uitgestorven olifantsvogels leefden
- Hoe het markeren van genen vóór de celdeling hun daaropvolgende reactivering versnelt
- Hoe de circadiane cyclus de reactie op medicijnen in planten beïnvloedt
- Wat is het geslacht en de soort in een wetenschappelijke naam?
- Leven vanaf de aarde kan tijdelijk overleven op Mars

- Nieuwe pekelprocessor verhoogt waterrecycling op International Space Station

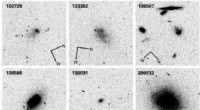
- Astronomen bepalen afstanden tot 18 dwergstelsels
- Inslagkraters onthullen details van Titans dynamische oppervlakteverwering

- Tweede uitlijningsvlak van zonnestelsel ontdekt

 Quick Science Fair Projectideeën
Quick Science Fair Projectideeën  Wat zijn de namen van 4 processen die van toestand veranderen als het gaat om gas, vloeibare en vaste stoffen?
Wat zijn de namen van 4 processen die van toestand veranderen als het gaat om gas, vloeibare en vaste stoffen?  Plaatsen om te graven voor edelstenen
Plaatsen om te graven voor edelstenen Waarom zijn er zoveel haaientanden op Venice Beach in Florida?
Waarom zijn er zoveel haaientanden op Venice Beach in Florida?  Slechts 7% van de Amerikaanse schooldistricten in armere, etnische minderheden gaan dit najaar weer open
Slechts 7% van de Amerikaanse schooldistricten in armere, etnische minderheden gaan dit najaar weer open Waarom is het lichaam gewichtloos in de ruimte?
Waarom is het lichaam gewichtloos in de ruimte?  Vrijwilligers streven ernaar om shutdown-chaos in Amerikaanse parken te voorkomen
Vrijwilligers streven ernaar om shutdown-chaos in Amerikaanse parken te voorkomen We vroegen meerval waarom ze mensen online voor de gek houden - het gaat niet om geld
We vroegen meerval waarom ze mensen online voor de gek houden - het gaat niet om geld
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

