
Wetenschap
Tweedimensionale Dirac-materialen:structuur, eigendommen, en zeldzaamheid
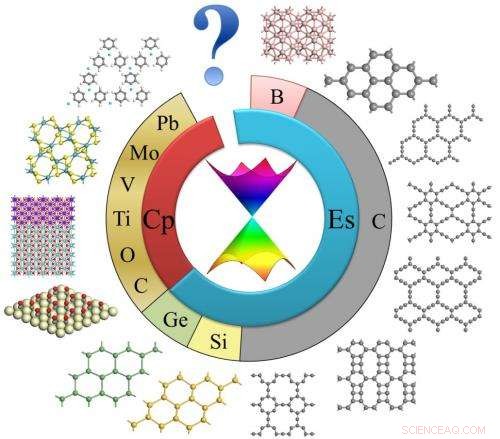
Schema van 2D-materialen met Dirac-kegels. Krediet:©Science China Press
grafeen, een tweedimensionale (2D) honingraatplaat samengesteld uit koolstofatomen, heeft wereldwijd intense belangstelling getrokken vanwege zijn uitstekende eigenschappen en veelbelovende vooruitzichten in zowel basis- als toegepaste wetenschap. De grote ontwikkeling van grafeen hangt nauw samen met de unieke elektronische structuur, dat is, Dirac kegels. De kegel die lineaire energiedispersie op Fermi-niveau vertegenwoordigt, geeft grafeen massaloze fermionen, wat leidt tot verschillende quantum Hall-effecten, ultra hoge vervoerder mobiliteit, en vele andere nieuwe verschijnselen en eigenschappen.
Dirac-kegel is speciaal, maar misschien niet uniek voor grafeen. Onlangs, er is voorspeld dat steeds meer 2D-materialen Dirac-kegels bevatten, zoals siliceen en germaneen (grafeenachtig silicium en germanium, respectievelijk), verschillende graphynes (sp-sp2 koolstofallotropen), enzovoort. Maar deze 2D Dirac-systemen zijn zo zeldzaam in vergelijking met de vele 2D-materialen. Een diep begrip van alle bekende 2D Dirac-systemen en een strategie om naar nieuwe te zoeken zijn nodig.
Een nieuw artikel gepubliceerd in Nationale wetenschappelijke recensie presenteerde de recente vooruitgang in theoretische studies van verschillende 2D Dirac-materialen.
In deze krant, de structurele en elektronische eigenschappen van grafeen, siliceen, Duits, grafiet, verschillende boor- en koolstofallotropen, overgangsmetaaloxiden, organische en organometaalkristallen, vierkante MoS2, en kunstmatige roosters (elektronengassen en ultrakoude atomen) werden samengevat. Zoals de auteur aangaf, "de meeste Dirac-materialen hebben ruimtelijke inversiesymmetrie", "Velen van hen zijn tweeledig en bestaan uit slechts één element", en "zeshoekige honingraatstructuur is gebruikelijk in atomaire Dirac-materialen". Aangezien "de Dirac-kegelstructuur grafeen massaloze fermionen geeft, wat leidt tot half-geheel getal/fractionele/fractale kwantum Hall-effecten, ultrahoge vervoerdermobiliteit", van andere 2D Dirac-systemen werd voorspeld dat ze vergelijkbare eigenschappen hebben, en sommige beschikken zelfs over nieuwe fysica die verder gaat dan grafeen.
Op basis van de bovenstaande discussies, de auteurs onderzochten verder hoe Dirac-punten bewegen en samensmelten in deze systemen. Ze zeiden dat spanning het Dirac-punt naar een nieuwe k (wederzijdse) locatie kan verplaatsen. Maar "wanneer twee Dirac-punten met tegengestelde Berry-fasen onder enige verstoring in de k-ruimte bewegen en op hetzelfde punt aankomen, ze fuseren en hun Berry-fasen vernietigen elkaar". de stelling van von Neumann-Wigner werd toegepast om de schaarste van 2D Dirac-systemen te verklaren. Vervolgens werden strenge eisen afgeleid voor een 2D-systeem om Dirac-kegels te bereiken, die verband houdt met de symmetrie, parameters, Fermi-niveau, en bandoverlapping.
Dit artikel merkte op dat "Dirac-kegels niet alleen de lineaire energiedispersie rond discrete punten zijn, maar ook singulariteiten in het spectrum van Hamiltonianen en topologisch beschermd zijn." De auteurs wezen erop:"Vooruitkijkend, we geloven dat er steeds meer 2D Dirac-materialen zullen worden ontdekt, en een grondig begrip van de bestaande omstandigheden van Dirac-kegels is zeer nuttig bij het zoeken naar / ontwerpen van nieuwe systemen."
 Hoe een chemische kettingreactie aan te wakkeren?
Hoe een chemische kettingreactie aan te wakkeren? Onzichtbare bloederige vingerafdrukken verlichten met een fluorescerend polymeer
Onzichtbare bloederige vingerafdrukken verlichten met een fluorescerend polymeer Onderzoekers creëren nieuw glaskeramisch materiaal van industriële verontreinigingen
Onderzoekers creëren nieuw glaskeramisch materiaal van industriële verontreinigingen Wetenschappers ontrafelen nieuwe inzichten in veelbelovend halfgeleidermateriaal
Wetenschappers ontrafelen nieuwe inzichten in veelbelovend halfgeleidermateriaal Apparaat verfijnt analyse van materialen voor brandstofcellen en batterijen
Apparaat verfijnt analyse van materialen voor brandstofcellen en batterijen
 Wetlands zijn essentieel voor nauwkeurige metingen van broeikasgassen in het noordpoolgebied
Wetlands zijn essentieel voor nauwkeurige metingen van broeikasgassen in het noordpoolgebied Visserij- en vervuilingsvoorschriften helpen koralen niet om met klimaatverandering om te gaan
Visserij- en vervuilingsvoorschriften helpen koralen niet om met klimaatverandering om te gaan NASA verzamelt nachtelijke beelden van Laura die een orkaan wordt
NASA verzamelt nachtelijke beelden van Laura die een orkaan wordt Zuurstof volgen in de Sargasso Seas 18 graden water
Zuurstof volgen in de Sargasso Seas 18 graden water Hooggerechtshof verwerpt EPA's beperkte visie op Clean Water Act
Hooggerechtshof verwerpt EPA's beperkte visie op Clean Water Act
Hoofdlijnen
- Hoe je geur te verbergen voor honden
- Bosplantages zijn een krachtige melange voor de koffieproductie
- Wetenschappers vinden bewijs van onze beste vrienden, honden, op dezelfde manier aangepast aan malaria in Afrika
- Onkruidverdelger veroorzaakt boze verdeeldheid onder Amerikaanse boeren
- Hittetolerante broccoli voor de toekomst
- VN schotelt vijgcactus voor als antwoord op voedselzekerheid
- Biologen maken kever met functioneel extra oog
- Wat zijn voorbeelden van homozygote dominanten?
- Je lichaam aan: een hittegolf
- Magnetische nanokubussen assembleren zichzelf tot spiraalvormige superstructuren

- Compressie of spanning - het materiaal zet altijd uit

- Wetenschappers observeren gericht energietransport tussen naburige moleculen in een nanomateriaal

- Een fluitje van een cent:arrays van lange nanobuisjes kunnen helpen bij het meten van terahertz-laservermogen

- Materiaalproductie uit deeltjes zet een grote stap voorwaarts

 Waarom pikt een babyfoon video op van de spaceshuttle?
Waarom pikt een babyfoon video op van de spaceshuttle?  Uit onderzoek blijkt dat de armen in de steden in de derde wereld politiek geëngageerd zijn
Uit onderzoek blijkt dat de armen in de steden in de derde wereld politiek geëngageerd zijn Nanocomponent is een kwantumsprong voor Deense natuurkundigen
Nanocomponent is een kwantumsprong voor Deense natuurkundigen Twitter zal inactieve accounts niet verwijderen na kritiek op profielen van dode gebruikers
Twitter zal inactieve accounts niet verwijderen na kritiek op profielen van dode gebruikers Nieuwe studie schat de CO2-voetafdruk van 13, 000 steden
Nieuwe studie schat de CO2-voetafdruk van 13, 000 steden NASA vindt dat Maysak extra-tropisch wordt
NASA vindt dat Maysak extra-tropisch wordt Hoe de afstand tussen twee punten op een curve te vinden
Hoe de afstand tussen twee punten op een curve te vinden Nieuwe manieren verkennen om thermische straling te beheersen
Nieuwe manieren verkennen om thermische straling te beheersen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

