
Wetenschap
Statistici ontwikkelen een efficiënte methode voor het vergelijken van hoogdimensionale gegevens
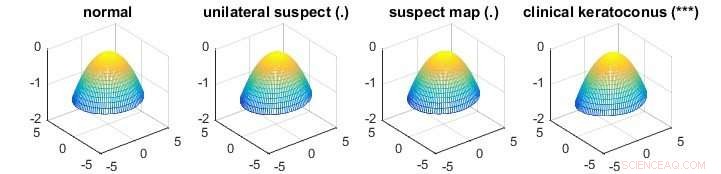
De afbeelding toont een toepassing van de nieuwe methode bij het identificeren van het verschil van gemiddelde hoornvliesoppervlakken met verschillende gradaties van de keratoconusziekte die ervoor zorgen dat hoornvliezen misvormd zijn. Symbolen tussen haakjes na de groepstitels geven de statistische significantie aan van het verschil tussen de geassocieerde groep en de normale groep, waarbij "***" een zeer significant verschil betekent en "." suggereert een niet-significant verschil. De corneale dataset is een voorbeeld van hoogdimensionale data. De normale groep heeft 43 hoornvliesoppervlakken terwijl de eenzijdige verdachte, verdachte kaart, en klinische keratoconusgroepen hebben 14, 21 en 72 hoornvliesoppervlakken respectievelijk. Elk hoornvliesoppervlak heeft 6, 912 metingen. De traditionele MANOVA-tests zijn niet geschikt voor dit probleem. Krediet:Nationale Universiteit van Singapore
MANOVA (multivariate variantieanalyse) is een veelgebruikte statistische methode bij gegevensanalyse om te bepalen of er een verschil is in de gemiddelden van verschillende groepen gegevens. Echter, de klassieke benadering is niet geschikt voor het analyseren van hoogdimensionale gegevens. Hoogdimensionale gegevens maken de traditionele MANOVA-methoden vaak ongeldig, omdat in een traditionele MANOVA, de dimensie wordt verondersteld vast te zijn en moet veel kleiner zijn dan het aantal waarnemingen. In een hoogdimensionale MANOVA-omgeving, dit is niet meer waar. Prof ZHANG Jin-Ting van de afdeling Statistiek en Toegepaste Kansrekening, NUS en zijn Ph.D. studenten hebben een nieuwe hoogdimensionale MANOVA-methode ontwikkeld die kan worden gebruikt om de gemiddelden van verschillende gegevensgroepen met hoogdimensionale gegevens efficiënt te vergelijken.
De nieuwe methode versoepelt veel wiskundige voorwaarden en beperkingen die in de literatuur worden opgelegd. Een daarvan is de aanname van homoscedasticiteit. Deze aanname is een wiskundige voorwaarde die vereist dat de gegevens van verschillende groepen dezelfde variatiepatronen hebben. Hun nieuwe methode lost ook de rekenproblemen op die betrokken zijn bij de praktische implementatie van MANOVA voor hoogdimensionale gegevens. Het doet dit door gebruik te maken van computationeel efficiënte matrixberekeningen op hoog niveau.
Hoewel het breed toepasbaar is en goed presteert voor veel real-life datasets, de voorgestelde methode kan in bepaalde situaties minder effectief zijn omdat de variatie- en correlatie-informatie van variabelen niet volledig wordt gebruikt. Bij het analyseren van gegevens over het hoornvliesoppervlak (zie onderstaande afbeelding), de bijbehorende covariantiematrix die de variatie- en correlatie-informatie uit de gegevens bevat, wordt berekend. Als het aantal hoornvliesoppervlakken groter is dan het aantal metingen van een hoornvliesoppervlak, de berekende covariantiematrix is inverteerbaar, wat betekent dat de teststatistiek kan worden verkregen met behulp van de traditionele MANOVA-test. In een hoog-dimensionale setting, dit is niet mogelijk omdat het aantal hoornvliesoppervlakken (150 =43+14+21+72 monsters) veel kleiner is dan het aantal metingen (6, 912 afmetingen). Echter, de variatie- en correlatie-informatie wordt nog steeds gedeeltelijk gebruikt bij het schatten van de parameters van de teststatistiek. Prof Zhang en zijn onderzoeksteam bestuderen dit om betere statistische methoden te ontwikkelen die dergelijke situaties aankunnen.
 "What Is Carbonate Buffering?
"What Is Carbonate Buffering? Wetenschappers gebruiken een teflonpijp om een goedkope, eenvoudige reactor voor de synthese van silicadeeltjes
Wetenschappers gebruiken een teflonpijp om een goedkope, eenvoudige reactor voor de synthese van silicadeeltjes Energie opslaan met eierschalen
Energie opslaan met eierschalen Nanostructurering verhoogt de efficiëntie van metaalvrije fotokatalysatoren met een factor 11
Nanostructurering verhoogt de efficiëntie van metaalvrije fotokatalysatoren met een factor 11 Krakende ontdekking:Japanse wetenschapper gebruikt eiwit voor schone energie
Krakende ontdekking:Japanse wetenschapper gebruikt eiwit voor schone energie
Hoofdlijnen
- Hoe zuurstofgas wordt geproduceerd tijdens fotosynthese?
- Wat gebeurt er in de interfase van de celcyclus?
- Onderzoekers ontdekken nieuwe manier om met stress om te gaan
- Het voordeel testen van linkshandig zijn in de sport
- Waar ligt de grens tussen fandom en obsessie?
- Studie onthult verschillen in belangrijke evoluties van het genoom van gewassen
- Kan slapen met een hersenschudding je doden?
- Sterke gastheren helpen parasieten zich verder te verspreiden
- Horror als Noorse goederentreinen meer dan 100 rendieren neermaaien
- De werkloosheid zal veel erger worden voordat het beter wordt, deskundige zegt:

- Schadenfreude:Jouw pijn is mijn winst

- Op elk moment in het leven, mensen brengen hun tijd door op 25 plaatsen

- Vroegmoderne mensen kookten zetmeelrijk voedsel in Zuid-Afrika, 170, 000 jaar geleden

- Godzijdank voor intrekbare snoeren,

 Een nieuwe draai geven aan Majorana-fermionen
Een nieuwe draai geven aan Majorana-fermionen Wie ontdekte Jodium 131 -
Wie ontdekte Jodium 131 -  Op prestaties gebaseerde beloning gekoppeld aan mentale gezondheidsproblemen van werknemers, studie toont
Op prestaties gebaseerde beloning gekoppeld aan mentale gezondheidsproblemen van werknemers, studie toont Hoe maak ik een 7e-graads schoolproject van een virusmodel?
Hoe maak ik een 7e-graads schoolproject van een virusmodel?  Wetenschappers maximaliseren de effectiviteit van platina in brandstofcellen
Wetenschappers maximaliseren de effectiviteit van platina in brandstofcellen Japan tekent bij SpaceX voor maanmissies
Japan tekent bij SpaceX voor maanmissies Klimaatmodellen met hoge resolutie presenteren alarmerende nieuwe projecties voor de VS
Klimaatmodellen met hoge resolutie presenteren alarmerende nieuwe projecties voor de VS kleine zat, grote ambities
kleine zat, grote ambities
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

