
Wetenschap
Er zijn slechts 15 mogelijke vijfhoekige tegels, onderzoek bewijst
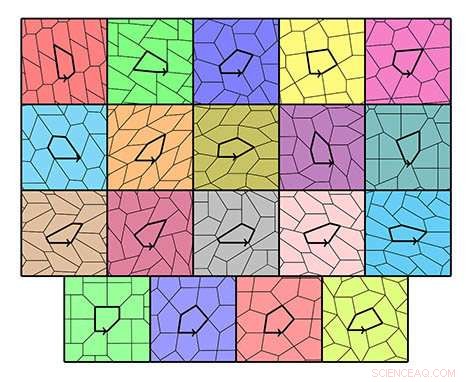
De 15 soorten vijfhoekige tegels en hun 4 specifieke soorten © Michael Rao, Laboratoire d'informatique du parallélisme. Credit:CNRS/Inria/ENS Lyon/Université Claude Bernard Lyon
Het vlak betegelen met een enkel patroon is een wiskundig probleem dat mensen al sinds de oudheid interesseert, met name voor de esthetische kwaliteit van tegels in mozaïek of tegelwerk. Een van de onopgeloste problemen op dit gebied die de wetenschappelijke gemeenschap sinds 1918 in verwarring brengen, is nu definitief opgelost dankzij Michaël Rao van het Laboratoire d'informatique du parallélisme (CNRS/Inria/ENS de Lyon/Université Claude Bernard Lyon 1). Met behulp van computertools kon hij aantonen dat er slechts 15 vijfzijdige patronen zijn die het vlak kunnen betegelen. Het onderzoek is nu beschikbaar op de Arxiv website.
Er zijn een aantal oplossingen voor het bekleden van een vloer met één enkele vorm, zoals driehoeken, vierkanten, rechthoeken, zeshoeken, enz. De uitputtende zoektocht naar alle convexe vormen die het vlak kunnen betegelen - een vorm met hoeken kleiner dan 180° die een hele muur kan bedekken zonder overlapping - werd geïnitieerd door Karl Reinhardt tijdens zijn proefschrift in 1918. Hij toonde aan dat alle driehoeken en vierhoeken kunnen het vlak betegelen, maar dat er maar 3 soorten zeshoeken waren die dat konden, en dat een veelhoek met zeven zijden of meer dat niet zou kunnen. Alleen de kwestie van de vijfhoeken bleef open.
15 soorten vijfhoeken werden ontdekt van 1918 tot 2015 als onderdeel van een enkelvoudig onderzoek:geïnitieerd door Reinhardt in 1918, het ging door een aantal wendingen, zoals nieuwe ontdekkingen door amateur-wiskundigen, tot de gemediatiseerde aankondiging in 2015 van een nieuwe 15e vorm 30 jaar na de 14e. Toch was de wetenschappelijke gemeenschap nog steeds niet in staat om te bepalen of er andere vormen van vijfhoeken waren die het vlak konden betegelen.
Michael Rao, een CNRS-onderzoeker aan het Laboratoire d'informatique du parallélisme (CNRS/Inria/ENS Lyon/Université Claude Bernard Lyon 1), heeft nu definitief aangetoond dat er slechts een eindige reeks families van vijfhoeken is waarmee rekening moet worden gehouden. Rao gebruikte een softwareprogramma om alle mogelijkheden te genereren, en toonde aan dat 371 families van vijfhoeken mogelijk het vliegtuig zouden kunnen betegelen. Vervolgens testte hij elk van deze families met een ander programma, en toonde aan dat slechts 19 soorten vijfhoeken voldeden aan de voorwaarden voor hoeken en zijlengtes die nodig zijn om het vlak te betegelen. Onder deze 19 soorten, 15 kwamen overeen met reeds bekende typen, en de vier andere bleken bijzondere gevallen van deze 15 typen te zijn. Bijgevolg, slechts 15 soorten tegels kunnen het vlak betegelen.
Rao was in staat om een eeuwenoud probleem op te lossen met zijn methodologie, en om nieuwe perspectieven te openen. Al deze convexe tegels kunnen het vlak periodiek betegelen (dat wil zeggen, de tegels herhalen zich oneindig). Toch is het nog niet bekend of er een tegel is die niet-periodiek betegelen toelaat. Gelukkig kunnen de meeste van deze technieken ook gebruikt worden voor niet-convexe polygonen, en zou dus als basis kunnen dienen voor het oplossen van een ander probleem op het gebied van tegels, beter bekend als het "Einstein-probleem" (van het Duitse "ein stein").
 Water traceren van rivier naar aquifer
Water traceren van rivier naar aquifer Orkaan Michael bereikt categorie 2, bedreigt zuidelijke VS
Orkaan Michael bereikt categorie 2, bedreigt zuidelijke VS Zuid-Chinese Zee blijkt verhoogde niveaus van antropogene oppervlaktestikstof te hebben
Zuid-Chinese Zee blijkt verhoogde niveaus van antropogene oppervlaktestikstof te hebben Klimaatverandering en smeltende gletsjers hebben zeer uiteenlopende gevolgen voor de Aziatische watervoorziening
Klimaatverandering en smeltende gletsjers hebben zeer uiteenlopende gevolgen voor de Aziatische watervoorziening Stranden verstikt met stinkend zeewier kunnen het nieuwe normaal zijn
Stranden verstikt met stinkend zeewier kunnen het nieuwe normaal zijn
Hoofdlijnen
- Moderne celtheorie
- Wat doet ethanol in een DNA-extractie?
- Uitbreiding tonijnquota stap achteruit voor instandhouding
- Wetenschappers ontdekken patronen van olifantenstroperij in Oost-Afrika
- Micro-evolutie: definitie, proces, micro versus macro & voorbeelden
- Metrowerk in Los Angeles onthult een reeks fossielen uit de ijstijd (update)
- Denken dieren rationeel? Onderzoeker suggereert dat rationele besluitvorming geen taal vereist
- Een studie schakelt over van genetische naar metabole analyse om het evolutionaire proces te reconstrueren
- Amerikaanse eiken delen een gemeenschappelijke noordelijke voorouder
- Armere gemeenschappen het zwaarst getroffen door incidenten met giftige vervuiling

- Natuur sluit zich aan bij wereldwijde academische staking tegen anti-zwart racisme

- Vragen over Amerikaanse musea Abraham Lincoln hoed

- Onderzoek toont aan dat stereotypen over daten nog steeds bestaan in de virtuele wereld

- Archeoloog ontdekt kruiwagen in Cornwall

 Onderzoek identificeert een eenvoudigere manier om te voorspellen hoe chemische verbindingen zullen interageren
Onderzoek identificeert een eenvoudigere manier om te voorspellen hoe chemische verbindingen zullen interageren Onze wereldwijde menselijke voetafdruk in kaart brengen
Onze wereldwijde menselijke voetafdruk in kaart brengen Het pannenkoekenprobleem oplossen
Het pannenkoekenprobleem oplossen Achtergrondwisseltechnologie geschikt voor mobiele telefoons aangekondigd
Achtergrondwisseltechnologie geschikt voor mobiele telefoons aangekondigd Onderzoekers evalueren wijzigingen in gegevensprivacy van de volkstelling in 2020
Onderzoekers evalueren wijzigingen in gegevensprivacy van de volkstelling in 2020 Verboden chemisch wapen VX is een krachtige moordenaar die blijft hangen
Verboden chemisch wapen VX is een krachtige moordenaar die blijft hangen Onafhankelijk, particuliere bedrijven vervuilen minder dan overheidsbedrijven, studie toont
Onafhankelijk, particuliere bedrijven vervuilen minder dan overheidsbedrijven, studie toont Skunk Water:een wapen dat stank gebruikt om menigten onder controle te houden
Skunk Water:een wapen dat stank gebruikt om menigten onder controle te houden
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

