
Wetenschap
Wat is de Fibonacci-reeks?

Bestaat er een magische vergelijking voor het universum? Waarschijnlijk niet, maar er zijn een aantal vrij algemene die we steeds weer tegenkomen in de natuurlijke wereld. Neem bijvoorbeeld de Fibonacci-reeks . Het is een reeks gestaag toenemende getallen waarbij elk getal (het Fibonacci-getal) de som is van de twee voorgaande getallen. (Over de wiskundige vergelijking zo meteen meer.)
De Fibonacci-reeks werkt ook in de natuur, als een overeenkomstige verhouding die verschillende patronen in de natuur weerspiegelt – denk aan de bijna perfecte spiraal van een nautilusschelp en de intimiderende werveling van een orkaan.
Mensen zijn waarschijnlijk al millennia op de hoogte van de Fibonacci-reeks; wiskundige ideeën rond dit interessante patroon dateren uit oude Sanskrietteksten van tussen 600 en 800 v.G.T. Maar in de moderne tijd hebben we het met alles in verband gebracht, van de obsessie van een middeleeuwse man met konijnen tot informatica en zonnebloempitten.
Inhoud- Fibonacci-getallen en hoe konijnen zich voortplanten
- Hoe de Fibonacci-reeks in de natuur werkt
- Misvattingen over de gulden snede
Fibonacci-getallen en hoe konijnen zich voortplanten

In 1202 vroeg de Italiaanse wiskundige Leonardo Pisano (ook bekend als Leonardo Fibonacci, wat 'zoon van Bonacci' betekent) zich af hoeveel konijnen een enkel stel ouders zou kunnen voortbrengen. Meer specifiek stelde Fibonacci de vraag:hoeveel paren konijnen kan een enkel paar konijnen in één jaar voortbrengen? Dit gedachte-experiment schrijft voor dat de vrouwelijke konijnen altijd paren baren, en elk paar bestaat uit één mannetje en één vrouwtje [bron:Ghose].
Denk er eens over na:twee pasgeboren konijnen worden in een afgesloten ruimte geplaatst waar de konijnen zich, nou ja, als konijnen beginnen voort te planten. Konijnen kunnen pas jongen krijgen als ze minimaal 1 maand oud zijn, dus de eerste maand blijft er slechts één koppel over. Aan het einde van de tweede maand baart het vrouwtje een nieuw paar, waardoor er in totaal twee paren overblijven.
Wanneer maand drie aanbreekt, brengt het oorspronkelijke paar konijnen nog een paar pasgeborenen voort, terwijl hun eerdere nakomelingen volwassen worden. Er blijven dan drie koppels konijnen over, waarvan er twee de volgende maand nog twee koppels zullen baren, zodat er in totaal vijf koppels konijnen zijn.
Hoeveel konijnen zouden er na een jaar zijn? Dat is het moment waarop de wiskundige vergelijking om de hoek komt kijken. Het is vrij eenvoudig, ondanks dat het complex klinkt.
De eerste Fibonacci-getallen luiden als volgt:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 en zo verder tot in het oneindige.
De wiskundige vergelijking die dit beschrijft ziet er als volgt uit:
Xn+2 =Xn+1 + XnKortom, elk geheel getal is de som van de voorgaande twee getallen. (Je kunt het concept toepassen op negatieve gehele getallen, maar we behandelen hier alleen de positieve gehele getallen.)
- Om 2 te vinden, telt u de twee getallen ervoor op (1+1)
- Om 3 te krijgen, telt u de twee cijfers ervoor op (1+2)
Deze reeks oneindige sommen staat bekend als de Fibonacci-reeks of de Fibonacci-reeks. De verhouding tussen de getallen in de Fibonacci-reeks (1,6180339887498948482...) wordt vaak de gulden snede of het gouden getal genoemd. De verhoudingen van opeenvolgende Fibonacci-getallen benaderen de gulden snede naarmate de getallen oneindig naderen.
Wil je zien hoe deze fascinerende getallen in de natuur tot uitdrukking komen? U hoeft niet naar uw plaatselijke dierenwinkel te gaan; het enige wat je hoeft te doen is om je heen kijken.
Hoe de Fibonacci-reeks in de natuur werkt

Hoewel sommige plantenzaden, bloemblaadjes en takken, enz. de Fibonacci-reeks volgen, weerspiegelt dit zeker niet hoe alle dingen in de natuurlijke wereld groeien. En het feit dat een reeks getallen kan worden toegepast op een verbazingwekkende verscheidenheid aan objecten, betekent niet noodzakelijkerwijs dat er een verband bestaat tussen cijfers en de werkelijkheid.
Net als bij numerologisch bijgeloof, zoals beroemde mensen die in reeksen van drie sterven, is toeval soms gewoon toeval.
Maar hoewel sommigen beweren dat de prevalentie van opeenvolgende Fibonacci-getallen in de natuur overdreven is, verschijnen ze vaak genoeg om te bewijzen dat ze bepaalde natuurlijk voorkomende patronen weerspiegelen. Je kunt deze meestal herkennen door de manier te bestuderen waarop verschillende planten groeien. Hier zijn een paar voorbeelden:
Zaadkoppen, dennenappels, fruit en groenten
Kijk naar de reeks zaden in het midden van een zonnebloem en je zult zien dat ze op een gouden spiraalpatroon lijken. Verbazingwekkend genoeg, als je deze spiralen meetelt, zal je totaal een Fibonacci-getal zijn. Verdeel de spiralen in linkse en rechtse spiralen en je krijgt twee opeenvolgende Fibonacci-getallen.
Op deze manier kun je spiraalvormige patronen in dennenappels, ananassen en bloemkool ontcijferen die ook de Fibonacci-reeks weerspiegelen [bron:Knott].
Bloemen en takken
Sommige planten drukken de Fibonacci-reeks uit in hun groeipunten, de plaatsen waar boomtakken zich vormen of splitsen. Eén stam groeit totdat er een tak ontstaat, waardoor er twee groeipunten ontstaan. Uit de hoofdstam komt dan weer een tak, waardoor er drie groeipunten ontstaan. Dan produceren de stam en de eerste tak nog twee groeipunten, wat het totaal op vijf brengt. Dit patroon zet zich voort en volgt de Fibonacci-getallen.
Als je bovendien het aantal bloemblaadjes van een bloem telt, zul je vaak merken dat het totaal een van de getallen in de Fibonacci-reeks is. Lelies en irissen hebben bijvoorbeeld drie bloemblaadjes, boterbloemen en wilde rozen hebben er vijf, delphiniums hebben acht bloemblaadjes, enzovoort.
Honingbijen
Een honingbijkolonie bestaat uit een koningin, een paar darren en veel werksters. De vrouwelijke bijen (koninginnen en werksters) hebben twee ouders:een dar en een koningin. Drones daarentegen komen uit onbevruchte eieren. Dit betekent dat ze maar één ouder hebben. Daarom geven de Fibonacci-getallen de stamboom van een drone weer in die zin dat hij één ouder, twee grootouders, drie overgrootouders, enzovoort heeft [bron:Knott].
Stormen
Stormsystemen zoals orkanen en tornado's volgen vaak de Fibonacci-reeks. De volgende keer dat je op de weerradar een orkaan in een spiraal ziet, kijk dan eens naar de onmiskenbare Fibonacci-spiraal in de wolken op het scherm.
Het menselijk lichaam
Kijk eens goed naar jezelf in de spiegel. Je zult merken dat de meeste van je lichaamsdelen de nummers één, twee, drie en vijf volgen. Je hebt één neus, twee ogen, drie segmenten aan elke ledemaat en vijf vingers aan elke hand. De verhoudingen en afmetingen van het menselijk lichaam kunnen ook worden onderverdeeld in termen van de gulden snede. DNA-moleculen volgen deze volgorde en zijn 34 angstrom lang en 21 angstrom breed voor elke volledige cyclus van de dubbele helix.
Waarom weerspiegelen zoveel natuurlijke patronen de Fibonacci-reeks?
Wetenschappers hebben eeuwenlang over deze vraag nagedacht. In sommige gevallen kan het verband louter toeval zijn. In andere situaties bestaat de ratio omdat dat specifieke groeipatroon zich als het meest effectief ontwikkelde. Bij planten kan dit een maximale blootstelling aan lichthongerige bladeren of een maximale zaadschikking betekenen.
Misvattingen over de gulden snede

Hoewel experts het erover eens zijn dat de Fibonacci-reeks in de natuur gebruikelijk is, bestaat er minder overeenstemming over de vraag of de Fibonacci-reeks in bepaalde gevallen van kunst en architectuur tot uitdrukking komt. Hoewel sommige boeken zeggen dat de Grote Piramide en het Parthenon (evenals enkele schilderijen van Leonardo da Vinci) zijn ontworpen met behulp van de gulden snede, blijkt dit bij het testen vals te zijn [bron:Markowsky].
Wiskundige George Markowsky wees erop dat zowel het Parthenon als de Grote Piramide delen hebben die niet in overeenstemming zijn met de gulden snede, iets dat is weggelaten door mensen die vastbesloten zijn te bewijzen dat Fibonacci-getallen in alles voorkomen. De term 'de gulden middenweg' werd in de oudheid gebruikt om iets aan te duiden dat toegang in beide richtingen vermeed, en sommige mensen hebben de gulden middenweg samengevoegd met de gulden snede, een recentere term die in de 19e eeuw ontstond.
Dat is interessant
We vieren Fibonacci-dag op 23 november niet alleen om het vergeten wiskundige genie Leonardo Fibonacci te eren, maar ook omdat wanneer de datum wordt geschreven als 23/11, de vier getallen een Fibonacci-reeks vormen. Van Leonardo Fibonacci wordt ook vaak gezegd dat hij heeft bijgedragen aan de verschuiving van Romeinse cijfers naar de Arabische cijfers die we vandaag de dag gebruiken.
Veel beantwoorde vragen
Wat is de uitleg van de Fibonacci-reeks?
De Fibonacci-reeks is een reeks getallen waarbij elk getal de som is van de twee voorgaande getallen. De eenvoudigste Fibonacci-reeks begint met 0, 1, 1, 2, 3, 5, 8, 13, 21, enzovoort.Veel meer informatie
Gerelateerde artikelen
- Hoe numerologie werkt
- Hoe kwantumzelfmoord werkt
- Heeft een surfer de theorie van alles ontdekt?
- Bestaat er een wiskundige formule voor het "bierbril"-effect?
- Volgt het Parthenon echt de gulden snede?
Bronnen
- Anderson, Matt, et al. "De Fibonacci-reeks." 1999. (14 juni 2008) http://library.thinkquest.org/27890/main
- "Fibonacci-getallen." Britannica Online Encyclopedie. 2008. (14 juni 2008) http://www.britannica.com/eb/article-9034168/Fibonacci-numbers
- "Fibonacci-getallen in de natuur." Wereld mysteries. (14 juni 2008) http://www.world-mysteries.com/sci_17.htm
- Caldwell, Chris. "Fibonacci-getallen." De Top Twintig. (14 juni 2008) http://primes.utm.edu/top20/page.php?id=39
- Ghose, Tia. "Wat is de Fibonacci-reeks?" 24 oktober 2018 (31 augustus 2021) https://www.livescience.com/37470-fibonacci-sequence.html
- Grist, Stan. "De verborgen structuur en Fibonacci-wiskunde." StanGrist.com. 2001. (14 juni 2008) http://www.stangrist.com/fibonacci.htm
- Knott, Ron. "Fibonacci-getallen in de natuur." Ron Knott's webpagina's over wiskunde. 28 maart 2008. (14 juni 2008) http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html
- Markowsky, George. "Misvattingen over de gulden snede." Het College Wiskunde Journal, Vol. 23, nr. 1. januari 1992. (31 augustus 2021) https://www.goldennumber.net/wp-content/uploads/George-Markowsky-Golden-Ratio-Misconceptions-MAA.pdf
 Rond de 35, 000 jaar geleden, Centraal Iberia had een toendra-steppelandschap
Rond de 35, 000 jaar geleden, Centraal Iberia had een toendra-steppelandschap Impact van grote vulkaanuitbarstingen in de afgelopen twee millennia op zowel het mondiale als het Chinese klimaat
Impact van grote vulkaanuitbarstingen in de afgelopen twee millennia op zowel het mondiale als het Chinese klimaat  Centraal-Europa:droge aprilmaanden maken de weg vrij voor zomerdroogte
Centraal-Europa:droge aprilmaanden maken de weg vrij voor zomerdroogte Red de natuur om onszelf te redden, VN-rapport pleit
Red de natuur om onszelf te redden, VN-rapport pleit Grote stijging van de economische kosten als de reductie van de uitstoot van broeikasgassen wordt uitgesteld
Grote stijging van de economische kosten als de reductie van de uitstoot van broeikasgassen wordt uitgesteld
Hoofdlijnen
- De beet uit slangengif halen
- Etiketten op verpakt vlees die de versheid weergeven, kunnen de houdbaarheidsdata vervangen, waardoor voedselverspilling wordt verminderd
- Nieuwe Vincetoxicum-soort gevonden in Yunnan
- Een dodelijke schimmel die het witte-neussyndroom veroorzaakt, kan een achilleshiel hebben, studie onthult
- Zoogdier waarvan lang gedacht werd dat het uitgestorven was in Australië duikt weer op
- De VS heeft de ergste uitbraak van vogelgriep in twee jaar op de eierboerderij in Iowa
- Hoe het gewasbeheer in de biologische tuinbouw te verbeteren
- Mijnwerkers schakelen over op bijenteelt
- Een onwaarschijnlijke held vergiftigen bij het afweren van exotische indringers?
- CERN:natuurkundigen melden ontdekking van uniek nieuw deeltje

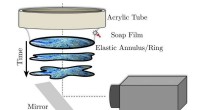
- Knikken tellen in een instortende ring om stabiliteit te voorspellen
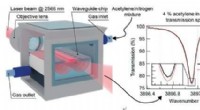
- Luchtgeleiding in optische golfgeleiders met vaste kern:een oplossing voor on-chip spoorgasspectroscopie
- Kunstmatige intelligentie helpt storingen in fusie-apparaten te voorkomen

- Wat zijn isotopen?

 Astrofysica-team verlicht de weg voor een nauwkeuriger model van het universum
Astrofysica-team verlicht de weg voor een nauwkeuriger model van het universum Chaos voorspellen met spuitbussen en AI
Chaos voorspellen met spuitbussen en AI Het perspectief op de oorsprong van enzymatische katalytische kracht veranderen
Het perspectief op de oorsprong van enzymatische katalytische kracht veranderen Bewegingsplanning voor automatisch rijden onder onzekerheid en met beperkt zicht
Bewegingsplanning voor automatisch rijden onder onzekerheid en met beperkt zicht India:in de frontlinie van klimaatverandering
India:in de frontlinie van klimaatverandering Een betere batterij bouwen met machine learning
Een betere batterij bouwen met machine learning De bijdrage van de kustlijn aan de klimaatverandering is mogelijk onderschat
De bijdrage van de kustlijn aan de klimaatverandering is mogelijk onderschat Elektronen geven elektrische lading aan de resistlaag
Elektronen geven elektrische lading aan de resistlaag
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

