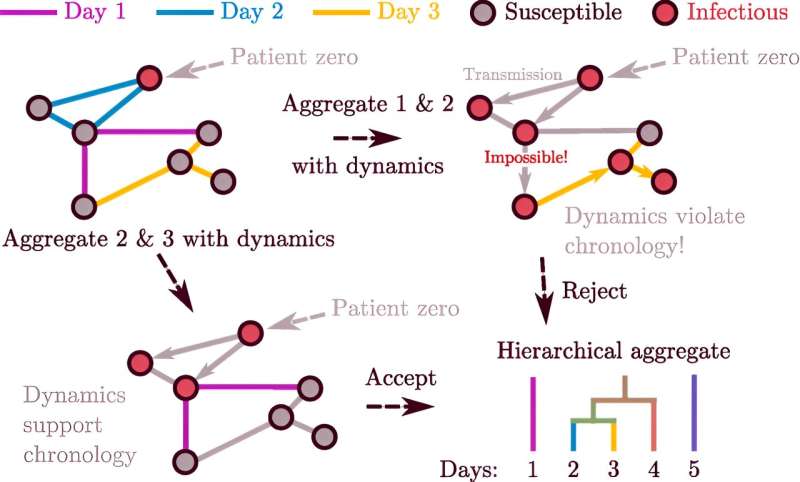
Netwerken kunnen veranderende systemen vertegenwoordigen, zoals de verspreiding van een epidemie of de groei van groepen in een bevolkingspopulatie. Maar de structuur van deze netwerken kan ook veranderen, naarmate links in de loop van de tijd verschijnen of verdwijnen. Om deze veranderingen beter te begrijpen, bestuderen onderzoekers vaak een reeks statische 'snapshots' die de structuur van het netwerk gedurende een korte periode vastleggen.

Netwerktheoretici hebben manieren gezocht om deze momentopnamen te combineren. In een nieuw artikel in Physical Review Letters beschrijft een drietal aan SFI aangesloten onderzoekers een nieuwe manier om statische momentopnamen samen te voegen tot kleinere clusters van netwerken, terwijl de dynamische aard van het systeem toch behouden blijft. Hun methode, geïnspireerd door een idee uit de kwantummechanica, omvat het testen van opeenvolgende paren netwerksnapshots om die te vinden waarvoor een combinatie het kleinste effect op de dynamiek van het systeem zou opleveren, en deze vervolgens te combineren.

Belangrijk is dat het kan bepalen hoe de geschiedenis van de netwerkstructuur zoveel mogelijk kan worden vereenvoudigd, terwijl de nauwkeurigheid behouden blijft. De wiskunde achter de methode is vrij eenvoudig, zegt hoofdauteur Andrea Allen, nu datawetenschapper bij Children's Hospital of Philadelphia.

"We zijn erg enthousiast dat we het kunnen delen, en het is een wonder dat niemand anders dit exacte idee de afgelopen tien jaar heeft gepubliceerd", zegt Allen. Ze werkte samen met SFI-professor Cris Moore, een natuurkundige en wiskundige, en Laurent Hébert-Dufresne, een complexiteitswetenschapper aan de Universiteit van Vermont en een voormalig SFI James S. McDonnell Foundation Fellow.

In het gepubliceerde artikel lijkt de methode niet ingewikkeld; in werkelijkheid is het in de loop der jaren zowel binnen als buiten SFI geëvolueerd. De samenwerking begon in 2015 toen Allen, destijds een bachelorstudent wiskunde, in de winter een maand lang SFI bezocht en vervolgens, in de zomer van 2016, terugkeerde om deel te nemen aan het Research Experiences for Undergraduates-programma (nu het Undergraduate Complexity Research-programma genoemd). .

Hébert-Dufresne had een grote dataset verkregen, verkregen uit satelliettelefoongegevens, die 'pings' van mobiele telefoons gebruikte om te laten zien hoe mensen zich verplaatsten. Hij was geïnteresseerd in het vinden van gemeenschappen, maar hij wilde ook kunnen meten of verschillende gemeenschappen een verschillende gegevensresolutie nodig hadden.

"Moeten bijvoorbeeld epidemische surveillancesystemen uniform zijn in alle gemeenschappen als we weten dat verschillende gemeenschappen verschillend gedrag vertonen?"

Die vraag leidde tot nog meer:​​"Op welk niveau kunnen we dit aggregeren terwijl we toch de verschillen behouden? En hoe weten we dat?" vraagt ​​Allen. "We willen de integriteit van het netwerk dat we proberen te bestuderen niet verliezen."

Ze schakelden Moore in om te brainstormen over ideeën om te weten welke verschillen belangrijk waren voor de algehele structuur, en welke minder belangrijk waren. Toen hebben ze het project na een tijdje op de plank gelegd.

Allen verliet de academische wereld om softwareontwikkelaar te worden en Hébert-Dufresne startte zijn eigen onderzoeksgroep in Vermont. Maar het zou een korte pauze zijn. Twee jaar later sloot Allen zich als afgestudeerde student aan bij de groep van Hébert-Dufresne in Vermont en ze gingen verder waar ze waren gebleven.

"We zeiden altijd:'laten we dit nu afronden'", zegt Allen. "Dit is acht jaar lang een grap geworden."

In het laatste zetje identificeerden de onderzoekers een eenvoudige manier om fouten te benaderen – en deze te gebruiken in opeenvolgende combinaties van netwerkparen. In het artikel gebruiken de onderzoekers de verspreiding van ziekten als maatstaf om de methode te beoordelen en te valideren.

“Stel dat er een pandemie uitbreekt”, zegt Moore. Als twee mensen – Alice en Bob – samenkomen, en vervolgens twee andere mensen – bijvoorbeeld Bob en Charlene – samenkomen, kan de ziekte zich van Alice naar Charlene verspreiden, maar niet andersom. De volgorde van deze links is van belang, wat betekent dat het misleidend is om ze in één momentopname te combineren (en ze te behandelen alsof ze gelijktijdig zijn).

De nieuwe methode ontleent een idee uit de kwantummechanica om dit soort fouten te identificeren. Op dat gebied kan de 'commutator' onthullen hoeveel orde van belang is bij berekeningen met zaken als energie en momentum. In de nieuwe toepassing gebruikten de onderzoekers een commutator om te beslissen hoeveel volgorde er toe doet, en wanneer het accuraat is om snapshots te combineren.

"Hierdoor kunnen we de geschiedenis van de netwerkstructuur zoveel mogelijk vereenvoudigen terwijl de nauwkeurigheid behouden blijft", zegt Moore. Het wijst ook op een manier om een ​​enorme, logge dataset te temmen in een kleinere, beheersbare set netwerken.

Allen zegt dat het kan worden uitgebreid naar andere dynamische systemen, zoals de verspreiding van informatie via een sociaal medianetwerk.

Meer informatie: Andrea J. Allen et al, De chronologie van een tijdelijk netwerk comprimeren met grafiekcommutators, Fysieke recensiebrieven (2024). DOI:10.1103/PhysRevLett.132.077402

Aangeboden door Santa Fe Instituut