Geometrie zit boordevol terminologie die precies beschrijft hoe verschillende punten, lijnen, oppervlakken en andere dimensionale elementen met elkaar omgaan. Soms zijn ze belachelijk ingewikkeld, zoals rhombicosidodecaëder, waarvan we denken dat het iets te maken heeft met "Star Trek"-wormgaten of polygonen. Of wat dacht je van de 12-zijdige dodecaëder?

Andere keren zijn we begiftigd met eenvoudigere termen, zoals overeenkomende hoeken .

Maar laten we, voordat we uitleggen wat ze zijn, snel een paar fundamentele concepten doornemen.

Herinner je je om te beginnen de definitie van een hoek? Het is wat je krijgt als twee stralen (lijnen met een enkel eindpunt) samenvoegen op een punt. De afstand tussen de twee stralen is de hoek .

Parallelle lijnen zijn twee lijnen op een tweedimensionaal vlak die elkaar nooit kruisen, hoe lang die lijnen ook worden.

Dan hebben we transversale lijnen . Dit is gewoon een chique manier om een ​​lijn een naam te geven die ten minste twee andere lijnen kruist.

Nu komen we in de magie. Want als een dwarslijn twee evenwijdige lijnen kruist, zijn de hoeken die uit deze snijpunten ontstaan ​​heel bijzonder. Dat wil zeggen, de paren hoeken aan dezelfde zijde van de transversale - en in dezelfde positie voor elke lijn die de transversale kruist - hebben dezelfde hoek. Met andere woorden, die hoeken zijn congruent (hetzelfde).

Als dat niet duidelijk is, kan de Merriam-Webster-definitie misschien helpen. Er staat dat corresponderende hoeken zijn:"elk paar hoeken die elk aan dezelfde kant liggen van een van de twee lijnen gesneden door een transversale en aan dezelfde kant van de transversale."

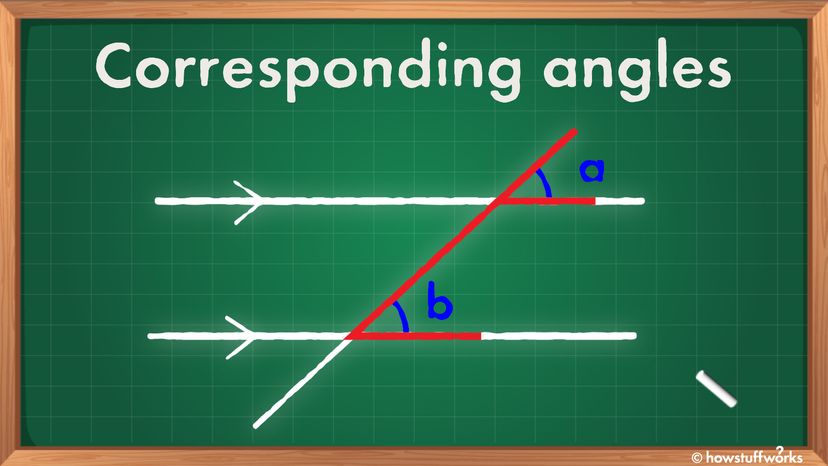
In de hoofdafbeelding hierboven zijn de overeenkomstige hoeken aangeduid met "a" en "b". Ze hebben dezelfde hoek. U kunt de corresponderende hoeken altijd vinden door te zoeken naar de F-formatie (voorwaarts of achterwaarts), rood gemarkeerd. Hier is nog een voorbeeld in de onderstaande afbeelding.

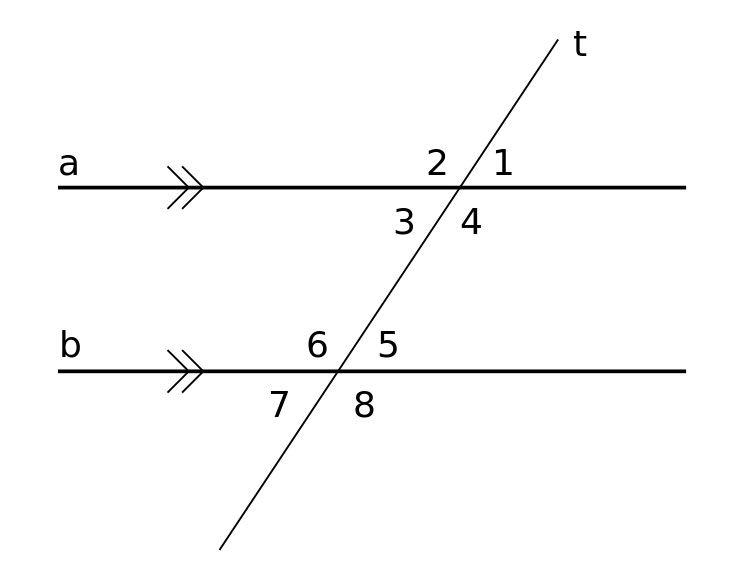
John Pauly is een wiskundeleraar op een middelbare school die verschillende manieren gebruikt om overeenkomstige hoeken aan zijn leerlingen uit te leggen. Hij zegt dat veel van zijn studenten moeite hebben om deze hoeken in een diagram te identificeren.

Hij zegt bijvoorbeeld om twee gelijkaardige driehoeken te nemen, driehoeken die dezelfde vorm hebben maar niet noodzakelijk dezelfde grootte. deze verschillende vormen kunnen worden getransformeerd. Mogelijk zijn ze verkleind, gedraaid of gereflecteerd.

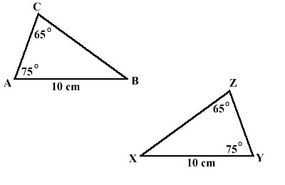
In bepaalde situaties kun je bepaalde dingen aannemen over overeenkomstige hoeken.

Neem bijvoorbeeld twee figuren die vergelijkbaar zijn, wat betekent dat ze dezelfde vorm hebben, maar niet noodzakelijk dezelfde grootte. Als twee figuren vergelijkbaar zijn, zijn hun overeenkomstige hoeken congruent (dezelfde). Dat is mooi, zegt Pauly, want hierdoor kunnen de figuren hun vorm behouden.

Hij zegt dat je een foto moet bedenken die je in een document wilt laten passen. "Je weet dat als je het formaat van de afbeelding aanpast, je uit een bepaalde hoek moet trekken. Als je dat niet doet, zullen de corresponderende hoeken niet congruent zijn, met andere woorden, het ziet er wankel en uit proportie uit. Dit werkt ook voor het omgekeerde. Als je een schaalmodel probeert te maken, weet je dat alle corresponderende hoeken hetzelfde (congruent) moeten zijn om die exacte kopie te krijgen die je zoekt."

Zoals bij alle wiskunde-gerelateerde concepten, willen leerlingen vaak weten waarom corresponderende hoeken nuttig zijn. "Nou, als je er zeker van wilt zijn dat je twee parallelle lijnen hebt, kun je dit trucje gebruiken," zei Pauly. "Waarom teken je niet een rechte lijn die beide lijnen onderschept en meet dan de bijbehorende hoeken." Als ze congruent zijn, weet je dat je je stukken goed hebt gemeten en gesneden. Het kennen van overeenkomstige hoeken is handig bij het bouwen van spoorwegen, hoogbouw en andere constructies.