
Wetenschap
Renormalisatiegroepsmethoden gebruiken om te bestuderen hoe de hersenen informatie verwerken

Dit is een momentopname uit een numerieke simulatie van het tweedimensionale Wilson-Cowan-model met stochastische invoer (Vgl. (3) in ons artikel). Gele (blauwe) pixels vertegenwoordigen hoge (lage) activiteit. Krediet:Tiberi et al.
Eerder neurowetenschappelijk onderzoek suggereert dat biologische neurale netwerken in de hersenen zichzelf kunnen organiseren in een kritieke toestand. In de natuurkunde is een kritieke toestand in wezen een punt dat de overgang markeert tussen geordende en ongeordende fasen van materie.
Onderzoekers van het Jülich Research Centre, RWTH Aachen University en Sorbonne Université hebben onlangs een theorie geïntroduceerd die zou kunnen helpen bij het verklaren van kriticiteit in de hersenen. Deze theorie, geïntroduceerd in een paper gepubliceerd in Physical Review Letters , is gebaseerd op een prototypische neurale veldentheorie, bekend als de 'stochastische Wilson-Cowan-vergelijking'.
"Eerdere werken hebben bewijs geleverd dat de hersenen op een kritiek punt werken", vertelden Lorenzo Tiberi, Jonas Stapmanns, Tobias Kühn, Thomas Luu, David Dahmen en Moritz Helias, de onderzoekers die het onderzoek uitvoerden, via e-mail aan Phys.org. . "Toch is het onduidelijk welke van de vele mogelijke soorten kritiekheden specifiek door de hersenen worden geïmplementeerd en hoe de laatste kritiekheid kunnen benutten voor optimale berekening."
Om de verschillende soorten kriticiteit te classificeren, gebruiken fysici doorgaans methoden binnen de zogenaamde renormalisatiegroep (RG). Dit zijn in wezen formele benaderingen die kunnen worden gebruikt om systematisch veranderingen in een fysiek systeem op verschillende schalen te onderzoeken.
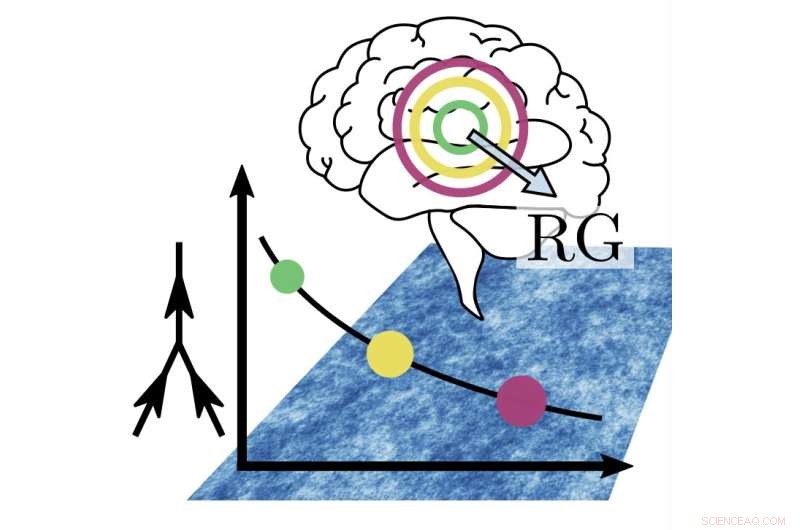
Abstracte figuur die de benadering van de renormalisatiegroep (RG) illustreert. Bij observatie van het systeem op steeds grovere lengteschalen (aangegeven door de concentrische cirkels en de pijl voor de hersenen), neemt de sterkte van de niet-lineaire interacties (weergegeven door het Feynman-diagram links) slechts langzaam af en blijft met name verschillend van nul zelfs op grote ruimtelijke schalen (curve met gekleurde stippen). Achtergrond:hetzelfde als figuur 1 maar ander kleurenschema. Krediet:Tiberi et al.
In hun studie pasten de onderzoekers deze traditionele methoden aan en integreerden ze met een prototypisch neuronaal veldmodel dat voor het eerst werd voorgesteld door Wilson en Cowan. Ze pasten ze vervolgens specifiek toe op het gebied van neurowetenschappen om de kriticiteit in biologische neurale netwerken te onderzoeken.
"In ons werk bestuderen we de gevestigde Wilson-Cowan-vergelijkingen met stochastische input, dus het model dat we gebruiken is niet nieuw", aldus Tiberi, Stapmanns en hun collega's. "Met behulp van RG-technieken komen we echter tot een origineel resultaat."
Om computationele taken te voltooien, cognitieve taken waarbij berekeningen betrokken zijn, moet het menselijk brein de invoergegevens die het ontvangt kunnen onthouden en vervolgens op complexe manieren combineren. Dit stelt het op zijn beurt in staat om de informatie te verwerken en het rekenprobleem op te lossen.
"We ontdekten dat de kriticiteit in het Wilson-Cowan neurale veldmodel van het Gell-Mann-Low-type is, dat, van alle soorten kriticiteit, specifiek een optimale balans biedt tussen het onthouden van invoergegevens en het combineren ervan op complexe manieren," Tiberi, Stapmanns en hun collega's zeiden.
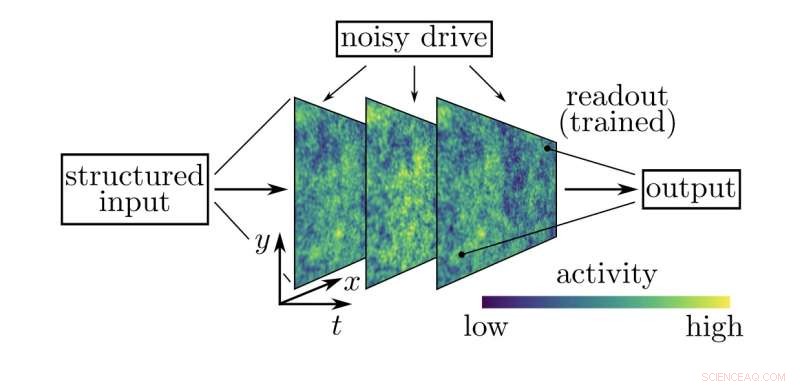
Figuur die het onderzoek naar de rekencapaciteiten van het model illustreert. Aan het systeem wordt een stimulus (gestructureerde input) toegevoegd (met ruimtelijke coördinaten x en y) die evolueert in de tijd t terwijl het netwerk ook wordt aangestuurd door stochastische input (lawaaierige drive). Een lineaire uitlezing wordt getraind om de invoerstimulus te reconstrueren of te classificeren op basis van een momentopname van de activiteit in het systeem. De reconstructietaak test het geheugen van het systeem, terwijl de classificatietaak niet-lineaire interacties vereist. Krediet:Tiberi et al.
Met behulp van RG-methoden zijn de onderzoekers erin geslaagd om de effecten van niet-lineaire interacties in het Wilson-Cowan-model te bestuderen, die cruciaal zijn om te begrijpen hoe de hersenen informatie verwerken. Dit is een opmerkelijke prestatie, aangezien de 'mean-field'-methoden die in het verleden door andere teams werden gebruikt, deze effecten niet konden vastleggen, vooral niet wanneer de interacties sterk genoeg zijn om de hersendynamiek op macroscopische schaal vorm te geven.
"We verwachten dat RG-methoden nuttig zullen zijn om andere niet-lineaire processen in neuronale netwerken te bestuderen", legde het team uit. "Bovendien leggen we verbanden met andere gebieden van de natuurkunde:het concept van Gell-Man-Low-kritiek komt voort uit de kwantumveldentheorie en het Kardar-Parisi-Zhang-model, dat nauw verwant is aan ons model, is oorspronkelijk gebruikt om dynamische groei te beschrijven van interfaces."
In de toekomst zou de theorie die door dit team van onderzoekers is geïntroduceerd, kunnen worden gebruikt om verschillende andere hersendynamieken en neurale processen te onderzoeken, die verder reiken dan kritiek. Bovendien zou het uiteindelijk de weg kunnen banen naar de introductie van andere theoretische constructies die natuurkunde en neurowetenschap samenvoegen.
"In de hersenen is de sterkte van verbindingen tussen neuronen zeer variabel in een mate dat het in een eerste benadering als willekeurig kan worden beschreven", voegde de onderzoekers eraan toe. "We zijn nu van plan onze methoden toe te passen op neurale modellen die deze functie bevatten en kijken welk effect dit heeft, indien aanwezig, op het type kriticiteit dat we vinden." + Verder verkennen
Neurale netwerken optimaliseren op een door de hersenen geïnspireerde computer
© 2022 Science X Network
 Race om kilowatt leegt Bosnisch meer
Race om kilowatt leegt Bosnisch meer Historische exemplaren benadrukken de sleutelrol die virussen spelen in Arctische ecosystemen
Historische exemplaren benadrukken de sleutelrol die virussen spelen in Arctische ecosystemen De bossen van Connecticut zijn tegenwoordig ver verwijderd van de torenhoge reuzen van weleer
De bossen van Connecticut zijn tegenwoordig ver verwijderd van de torenhoge reuzen van weleer Nieuwe richtlijnen om China's ernstige luchtvervuilingsprobleem aan te pakken
Nieuwe richtlijnen om China's ernstige luchtvervuilingsprobleem aan te pakken Nieuwe zoetwaterdatabase vertelt het verhaal van de waterkwaliteit voor 12K-meren wereldwijd
Nieuwe zoetwaterdatabase vertelt het verhaal van de waterkwaliteit voor 12K-meren wereldwijd
Hoofdlijnen
- Bacteriën als pacemaker voor de darm
- Honden likken hun mond om te communiceren met boze mensen
- Onderzoekers testen probiotica in voeding en supplementen
- Delen van een dierencel voor kinderen
- Het verschil tussen glycolyse en gluconeogenese
- Wanneer vissen:Timing is belangrijk voor vissen die migreren om zich voort te planten
- Waar ligt de grens tussen fandom en obsessie?
- Studie suggereert nieuw mechanisme voor lipidetransporter
- Wat zijn drie primaire doelen van mitose?
- Ultrasnel op glasvezel gebaseerd elektronenkanon om atomaire bewegingen te onthullen
- Beeldvorming met hoge resolutie met conventionele microscopen
- Gecorreleerde fotonen gebruiken om röntgenbeeldvorming te verbeteren
- Onderzoek naar de dynamiek van foto-emissie

- Een microscoop met hoge resolutie gemaakt van LEGO en telefoonbits
 Salamanderkenmerken
Salamanderkenmerken Laatste Facebook-controverse zet nummer twee Sandberg in vuur en vlam
Laatste Facebook-controverse zet nummer twee Sandberg in vuur en vlam Ontwikkeling van elektrodemateriaal dat de efficiëntie van zoutgehaltegradiëntenergie verbetert
Ontwikkeling van elektrodemateriaal dat de efficiëntie van zoutgehaltegradiëntenergie verbetert Antarctica:terugkeer van de Weddell-polynya ondersteunt het klimaatmodel van Kiel
Antarctica:terugkeer van de Weddell-polynya ondersteunt het klimaatmodel van Kiel Nieuw kunstmatige-intelligentiesysteem evolueert automatisch om internetcensuur te omzeilen
Nieuw kunstmatige-intelligentiesysteem evolueert automatisch om internetcensuur te omzeilen Berekenen van drijfvermogen voor een pijp
Berekenen van drijfvermogen voor een pijp  Geo-engineering, andere technologieën zullen klimaatproblemen niet oplossen
Geo-engineering, andere technologieën zullen klimaatproblemen niet oplossen Gigantische jet bespioneerd vanuit zwart gat in vroeg heelal
Gigantische jet bespioneerd vanuit zwart gat in vroeg heelal
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

