
Wetenschap
Kwantumsprong voor snelheidslimieten
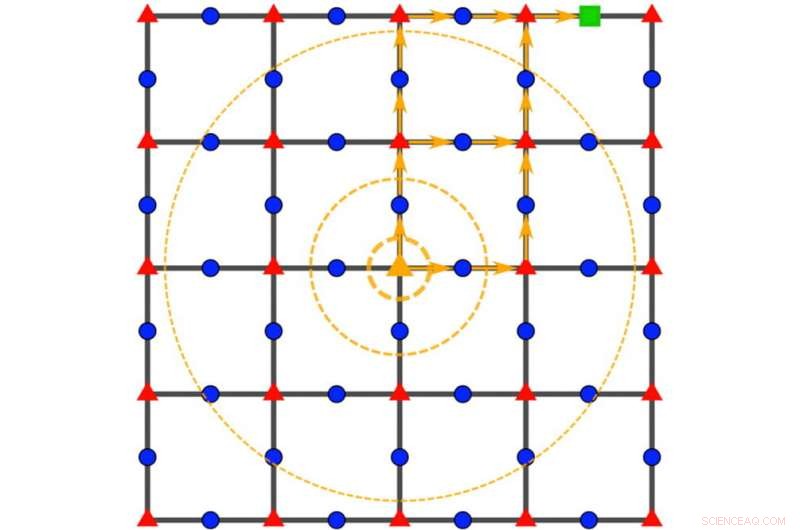
Een Wang-Hazzard-commutativiteitsgrafiek legt de microscopische details vast van de wiskundige functies die natuurkundigen doorgaans gebruiken om energie in kwantumsystemen te beschrijven. het reduceren van de berekening van kwantumsnelheidslimieten tot een vergelijking met slechts twee ingangen. Krediet:Zhiyuan Wang/Rice University
De snelheidslimieten van de natuur staan niet op verkeersborden, maar natuurkundigen van Rice University hebben een nieuwe manier ontdekt om ze af te leiden die beter is - oneindig beter, in sommige gevallen—dan eerdere methoden.
"De grote vraag is 'Hoe snel kan iets - informatie, massa, energie - bewegen in de natuur?'" zei Kaden Hazzard, een theoretische kwantumfysicus bij Rice. "Het blijkt dat als iemand je een materiaal overhandigt, het is ongelooflijk moeilijk, in het algemeen, om de vraag te beantwoorden."
In een onderzoek dat vandaag is gepubliceerd in het tijdschrift American Physical Society: PRX Quantum , Hazzard en Rice afgestudeerde student Zhiyuan Wang beschrijven een nieuwe methode voor het berekenen van de bovengrens van snelheidslimieten in kwantummaterie.
"Op een fundamenteel niveau deze grenzen zijn veel beter dan wat voorheen beschikbaar was, " zei Hazzard, een assistent-professor natuurkunde en sterrenkunde en lid van het Rice Center for Quantum Materials. "Deze methode levert vaak grenzen op die tien keer nauwkeuriger zijn, en het is niet ongebruikelijk dat ze 100 keer nauwkeuriger zijn. In sommige gevallen, de verbetering is zo dramatisch dat we eindige snelheidslimieten vinden waar eerdere benaderingen oneindige voorspelden."
De ultieme snelheidslimiet van de natuur is de snelheid van het licht, maar in bijna alle materie om ons heen, de snelheid van energie en informatie is veel langzamer. Vaak, het is onmogelijk om deze snelheid te beschrijven zonder rekening te houden met de grote rol van kwantumeffecten.
In de jaren zeventig, natuurkundigen bewezen dat informatie veel langzamer moet bewegen dan de lichtsnelheid in kwantummaterialen, en hoewel ze geen exacte oplossing voor de snelheden konden berekenen, natuurkundigen Elliott Lieb en Derek Robinson pionierden met wiskundige methoden om de bovengrenzen van die snelheden te berekenen.
"Het idee is dat zelfs als ik je de exacte topsnelheid niet kan vertellen, mag ik je vertellen dat de topsnelheid lager moet zijn dan een bepaalde waarde, Hazzard zei. "Als ik een 100% garantie kan geven dat de werkelijke waarde lager is dan die bovengrens, dat kan enorm handig zijn."
Hazzard zei dat natuurkundigen al lang weten dat sommige van de door de Lieb-Robinson-methode geproduceerde grenzen "belachelijk onnauwkeurig" zijn.
"Het zou kunnen zeggen dat informatie minder dan 100 mijl per uur in een materiaal moet bewegen toen de echte snelheid werd gemeten met 0,01 mijl per uur, "zei hij. "Het is niet verkeerd, maar het is niet erg handig."
De nauwkeuriger grenzen die in het PRX Quantum-papier worden beschreven, werden berekend met een methode die Wang heeft gemaakt.
"We hebben een nieuw grafisch hulpmiddel uitgevonden waarmee we rekening kunnen houden met de microscopische interacties in het materiaal in plaats van alleen te vertrouwen op grovere eigenschappen zoals de roosterstructuur, ' zei Wang.
Hazzard zei Wang, een derdejaarsstudent, heeft een ongelooflijk talent voor het synthetiseren van wiskundige relaties en het herschikken ervan in nieuwe termen.
"Als ik zijn berekeningen controleer, Ik kan stap voor stap gaan, doorloop de berekeningen en kijk of ze kloppen, "Zei Hazzard. "Maar om er echt achter te komen hoe je van punt A naar punt B komt, welke reeks stappen je moet nemen als er een oneindige verscheidenheid aan dingen is die je bij elke stap zou kunnen proberen, de creativiteit is gewoon geweldig voor mij."
De Wang-Hazzard-methode kan worden toegepast op elk materiaal dat bestaat uit deeltjes die in een discreet rooster bewegen. Dat omvat vaak bestudeerde kwantummaterialen zoals supergeleiders bij hoge temperaturen, topologische materialen, zware fermionen en andere. In elk van deze, het gedrag van de materialen komt voort uit interacties van miljarden op miljarden deeltjes, waarvan de complexiteit verder gaat dan directe berekening.
Hazzard zei dat hij verwacht dat de nieuwe methode op verschillende manieren zal worden gebruikt.
"Naast de fundamentele aard hiervan, het kan nuttig zijn om de prestaties van kwantumcomputers te begrijpen, in het bijzonder om te begrijpen hoe lang het duurt om belangrijke problemen op het gebied van materialen en chemie op te lossen, " hij zei.
Hazzard zei dat hij er zeker van is dat de methode ook zal worden gebruikt om numerieke algoritmen te ontwikkelen, omdat Wang heeft aangetoond dat het rigoureuze grenzen kan stellen aan de fouten die worden veroorzaakt door vaak gebruikte numerieke technieken die het gedrag van grote systemen benaderen.
Een populaire techniek die natuurkundigen al meer dan 60 jaar gebruiken, is om een groot systeem te benaderen door een klein systeem dat door een computer kan worden gesimuleerd.
"We tekenen een kleine doos rond een eindig stuk, simuleer dat en hoop dat dat genoeg is om het gigantische systeem te benaderen, "Zei Hazzard. "Maar er is geen rigoureuze manier geweest om de fouten in deze benaderingen te begrenzen."
De Wang-Hazzard-methode voor het berekenen van grenzen zou daartoe kunnen leiden.
"Er is een intrinsiek verband tussen de fout van een numeriek algoritme en de snelheid van informatieverspreiding, "Wan legde uit, met behulp van het geluid van zijn stem en de muren in zijn kamer om de link te illustreren.
"Het eindige stuk heeft randen, net zoals mijn kamer muren heeft. Als ik spreek, het geluid wordt weerkaatst door de muur en weerkaatst naar mij. In een oneindig systeem, er is geen rand, dus er is geen echo."
In numerieke algoritmen, fouten zijn het wiskundige equivalent van echo's. Ze weerkaatsen vanaf de randen van de eindige doos, en de reflectie ondermijnt het vermogen van de algoritmen om het oneindige geval te simuleren. Hoe sneller informatie door het eindige systeem gaat, hoe korter de tijd dat het algoritme het oneindige getrouw weergeeft.
Hazzard zei dat hij, Wang en anderen in zijn onderzoeksgroep gebruiken hun methode om numerieke algoritmen te maken met gegarandeerde foutbalken.
"We hoeven niet eens de bestaande algoritmen te veranderen om strikte, gegarandeerde foutbalken op de berekeningen, " zei hij. "Maar je kunt het ook omdraaien en dit gebruiken om betere numerieke algoritmen te maken. Dat zijn we aan het onderzoeken, en andere mensen zijn ook geïnteresseerd om deze te gebruiken."
 Onderzoekers gebruiken schuifkrachten om zelf-geassembleerde supramoleculaire hydrogel te maken
Onderzoekers gebruiken schuifkrachten om zelf-geassembleerde supramoleculaire hydrogel te maken Isotopen zoeken
Isotopen zoeken  AI- en NMR-spectroscopie bepalen in recordtijd de configuratie van atomen
AI- en NMR-spectroscopie bepalen in recordtijd de configuratie van atomen Negatieve ontwerpstrategieën voor thermische uitzetting in metaal-organische raamwerken
Negatieve ontwerpstrategieën voor thermische uitzetting in metaal-organische raamwerken Twee beter dan één:scheikundigen bevorderen duurzame batterijtechnologie
Twee beter dan één:scheikundigen bevorderen duurzame batterijtechnologie
 Biologische voeding biedt aanzienlijke milieuvoordelen voor plantrijke diëten
Biologische voeding biedt aanzienlijke milieuvoordelen voor plantrijke diëten Reeks aardbevingen in het oosten van Taiwan richt enige schade aan
Reeks aardbevingen in het oosten van Taiwan richt enige schade aan Orkanen voorkomen met luchtbellen
Orkanen voorkomen met luchtbellen NASA ziet tropische depressie 30W-vorm in de noordwestelijke Stille Oceaan
NASA ziet tropische depressie 30W-vorm in de noordwestelijke Stille Oceaan Lapis Lazulis Koningsblauwe kleur werd ooit als goddelijk beschouwd
Lapis Lazulis Koningsblauwe kleur werd ooit als goddelijk beschouwd
Hoofdlijnen
- mensen, in tegenstelling tot apen, verander de concurrentiesituatie in een coöperatieve
- Staan we allemaal af van een gemeenschappelijke vrouwelijke voorouder?
- Vergelijk en vergelijk DNA en RNA
- Relatie tussen DNA-basen Genen, eiwitten en eigenschappen
- Welke oorzaken smeren bij elektroforese?
- Biogeografie: definitie, theorie, bewijs & voorbeelden
- Landen in de Stille Oceaan kunnen door klimaatverandering 50 - 80% van de vis in lokale wateren verliezen
- In het verleden werpen helpt de toekomst van de visserij te onthullen
- Cellulaire ademhaling: definitie, vergelijking en stappen
- Wetenschappers vinden makkelijker uit, goedkopere manier om zwaartekracht te meten

- Natuurkundigen maken tourniquet voor fotonen

- Licht werpen op de rol van ongewenste onzuiverheden in galliumnitride-halfgeleiders

- Spin regelen voor geheugenopslag

- Om een machine ter grootte van een atoom te maken, je hebt een kwantummechanica nodig

 Hoe kan de geneeskunde de loonkloof tussen mannen en vrouwen dichten?
Hoe kan de geneeskunde de loonkloof tussen mannen en vrouwen dichten? Hoe Quartiles
Hoe Quartiles Hoe steenijzermeteorieten ontstaan
Hoe steenijzermeteorieten ontstaan Antarctica voert zeespiegelstijging op
Antarctica voert zeespiegelstijging op Door zonlicht en afvalwaternitraat te combineren om 's werelds nummer 2 chemisch te maken
Door zonlicht en afvalwaternitraat te combineren om 's werelds nummer 2 chemisch te maken Het verleden gebruiken om toekomstige constructies vorm te geven:platen die rocken, kantelen en rollen
Het verleden gebruiken om toekomstige constructies vorm te geven:platen die rocken, kantelen en rollen Soorten grasland-ecosystemen
Soorten grasland-ecosystemen  MoS2-transistor die kan worden gebruikt met buigbare OLED-schermen
MoS2-transistor die kan worden gebruikt met buigbare OLED-schermen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

