Wetenschap
Een nieuw wiskundig model voorspelt een knopenstabiliteit

Een voorbeeld van bovenhandse knopen. Krediet:Massachusetts Institute of Technology
tijdens het zeilen, rotsklimmen, bouw, en elke activiteit die het vastzetten van touwen vereist, van bepaalde knopen is bekend dat ze sterker zijn dan andere. Elke doorgewinterde zeiler weet, bijvoorbeeld, dat ene type knoop een laken aan een voorzeil zal bevestigen, terwijl een ander beter is om een boot op een paal te spannen.
Maar wat precies de ene knoop stabieler maakt dan de andere, is niet goed begrepen, tot nu.
MIT-wiskundigen en ingenieurs hebben een wiskundig model ontwikkeld dat voorspelt hoe stabiel een knoop is, gebaseerd op een aantal belangrijke eigenschappen, inclusief het aantal kruisingen en de richting waarin de touwsegmenten draaien als de knoop strak wordt getrokken.
"Deze subtiele verschillen tussen knopen bepalen kritisch of een knoop sterk is of niet, " zegt Jörn Dunkel, universitair hoofddocent wiskunde aan het MIT. "Met dit model je zou naar twee knopen moeten kunnen kijken die bijna identiek zijn, en kunnen zeggen welke de beste is."
"Empirische kennis die door de eeuwen heen is verfijnd, heeft uitgekristalliseerd wat de beste knopen zijn, " voegt Mathias Kolle toe, de Rockwell International Career Development Associate Professor aan het MIT. "En nu laat het model zien waarom."
Dunkel, Kolle, en Ph.D. studenten Vishal Patil en Joseph Sandt hebben hun resultaten vandaag gepubliceerd in het tijdschrift Wetenschap .
De kleur van de druk
in 2018, Kolle's groep ontwikkelde rekbare vezels die van kleur veranderen als reactie op spanning of druk. De onderzoekers toonden aan dat wanneer ze aan een vezel trokken, zijn tint veranderde van de ene kleur van de regenboog in de andere, vooral in gebieden die de grootste stress of druk hebben ervaren.
Kolle, een universitair hoofddocent werktuigbouwkunde, werd uitgenodigd door de wiskundeafdeling van MIT om een lezing te geven over de vezels. Dunkel zat in het publiek en begon een idee te bedenken:wat als de drukgevoelige vezels zouden kunnen worden gebruikt om de stabiliteit in knopen te bestuderen?
Wiskundigen zijn al lang geïntrigeerd door knopen, zozeer zelfs dat fysieke knopen een heel deelgebied van de topologie hebben geïnspireerd dat bekend staat als knopentheorie - de studie van theoretische knopen waarvan de uiteinden, in tegenstelling tot echte knopen, worden samengevoegd tot een doorlopend patroon. In de knooptheorie, wiskundigen proberen een knoop in wiskundige termen te beschrijven, samen met alle manieren waarop het kan worden gedraaid of vervormd met behoud van zijn topologie, of algemene geometrie.
"In de wiskundige knooptheorie, je gooit alles weg wat met mechanica te maken heeft, " zegt Dunkel. "Het maakt je niet uit of je een stijve of een zachte vezel hebt - het is dezelfde knoop vanuit het oogpunt van een wiskundige. Maar we wilden zien of we iets konden toevoegen aan de wiskundige modellering van knopen dat hun mechanische eigenschappen verklaart, om te kunnen zeggen waarom de ene knoop sterker is dan de andere."
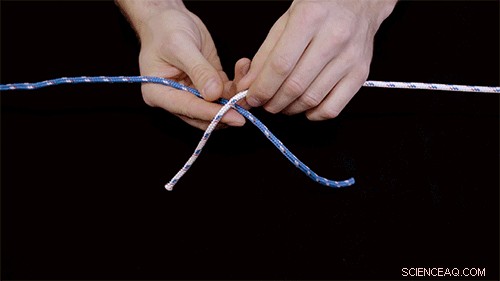
Een voorbeeld van een rifknoop. Krediet:Massachusetts Institute of Technology
Spaghetti natuurkunde
Dunkel en Kolle werkten samen om te bepalen wat de stabiliteit van een knoop bepaalt. Het team gebruikte eerst Kolle's vezels om verschillende knopen te leggen, inclusief de klaverblad- en achtknopen-configuraties die Kolle bekend waren, wie is een fervent zeiler, en aan rotsklimmende leden van de groep van Dunkel. Ze fotografeerden elke vezel, opmerkend waar en wanneer de vezel van kleur veranderde, samen met de kracht die op de vezel werd uitgeoefend toen deze strak werd getrokken.
De onderzoekers gebruikten de gegevens van deze experimenten om een model te kalibreren dat de groep van Dunkel eerder implementeerde om een ander type vezel te beschrijven:spaghetti. In dat model is Patil en Dunkel beschreven het gedrag van spaghetti en andere flexibele, touwachtige structuren door elke streng te behandelen als een ketting van kleine, discreet, veer-verbonden kralen. De manier waarop elke veer buigt en vervormt, kan worden berekend op basis van de kracht die op elke individuele veer wordt uitgeoefend.
Kolles leerling Joseph Sandt had eerder een kleurenkaart gemaakt op basis van experimenten met de vezels, die de kleur van een vezel correleert met een bepaalde druk die op die vezel wordt uitgeoefend. Patil en Dunkel hebben deze kleurenkaart verwerkt in hun spaghettimodel, vervolgens gebruikten ze het model om dezelfde knopen te simuleren die de onderzoekers fysiek hadden gemaakt met behulp van de vezels. Toen ze de knopen in de experimenten vergeleken met die in de simulaties, ze ontdekten dat het kleurenpatroon in beide vrijwel hetzelfde was - een teken dat het model nauwkeurig de verdeling van spanning in knopen simuleerde.
Met vertrouwen in hun model, Patil simuleerde toen meer gecompliceerde knopen, noteren welke knopen meer druk ondervonden en daardoor sterker waren dan andere knopen. Zodra ze knopen categoriseerden op basis van hun relatieve sterkte, Patil en Dunkel zochten een verklaring waarom bepaalde knopen sterker waren dan andere. Om dit te doen, ze maakten eenvoudige schema's voor de bekende oma, rif, dief, en verdriet knopen, samen met meer gecompliceerde, zoals de carrick, zeppelin, en Alpenvlinder.
Elk knoopdiagram toont het patroon van de twee strengen in een knoop voordat deze strak wordt getrokken. De onderzoekers hebben de richting van elk segment van een streng opgenomen terwijl het wordt getrokken, samen met waar strengen elkaar kruisen. Ze noteerden ook de richting waarin elk segment van een streng draait als een knoop wordt aangehaald.
Bij het vergelijken van de diagrammen van knopen van verschillende sterktes, konden de onderzoekers algemene "telregels, " of kenmerken die de stabiliteit van een knoop bepalen. Kortom, een knoop is sterker als hij meer strengkruisingen heeft, evenals meer "draaifluctuaties" -veranderingen in de draairichting van het ene strengsegment naar het andere.
Bijvoorbeeld, als een vezelsegment bij een kruising naar links wordt gedraaid en bij een aangrenzende kruising naar rechts wordt gedraaid als een knoop strak wordt getrokken, dit zorgt voor een draaifluctuatie en dus tegengestelde wrijving, wat stabiliteit aan een knoop toevoegt. Indien, echter, het segment wordt geroteerd in dezelfde richting op twee aangrenzende kruisingen, er is geen draaifluctuatie, en de streng heeft meer kans om te roteren en te slippen, waardoor een zwakkere knoop ontstaat.
Ze ontdekten ook dat een knoop sterker kan worden gemaakt als hij meer "circulaties, " die ze definiëren als een gebied in een knoop waar twee evenwijdige strengen tegen elkaar in tegenovergestelde richtingen, als een cirkelvormige stroom.
Door rekening te houden met deze eenvoudige telregels, kon het team uitleggen waarom een rifknoop, bijvoorbeeld, is sterker dan een oma knoop. Hoewel de twee bijna identiek zijn, de rifknoop heeft een hoger aantal twistfluctuaties, waardoor het een stabielere configuratie wordt. Hetzelfde, de zeppelinknoop, vanwege de iets hogere circulaties en draaifluctuaties, is sterker, hoewel mogelijk moeilijker los te maken, dan de Alpenvlinder - een knoop die vaak wordt gebruikt bij klimmen.
"Als je een familie van vergelijkbare knopen neemt, waaruit empirische kennis er één uitkiest als "de beste, "nu kunnen we zeggen waarom het dit onderscheid zou kunnen verdienen, " zegt Kolle, die zich het nieuwe model voorstelt, kan worden gebruikt om knopen van verschillende sterktes te configureren voor specifieke toepassingen. "We kunnen knopen tegen elkaar uitspelen voor gebruik bij het hechten, het zeilen, klimmen, en constructie. Het is fantastisch."
Dit verhaal is opnieuw gepubliceerd met dank aan MIT News (web.mit.edu/newsoffice/), een populaire site met nieuws over MIT-onderzoek, innovatie en onderwijs.
 Damp drijft een vloeistof-vaste overgang in een moleculair systeem aan
Damp drijft een vloeistof-vaste overgang in een moleculair systeem aan Team haalt inspiratie uit natuurlijke wonderen om nieuwe materialen te maken
Team haalt inspiratie uit natuurlijke wonderen om nieuwe materialen te maken Wetenschappers lossen 3D-structuur van cystic fibrosis-eiwit op in actieve, inactieve staten
Wetenschappers lossen 3D-structuur van cystic fibrosis-eiwit op in actieve, inactieve staten Een biosensor voor het meten van extracellulaire waterstofperoxideconcentraties
Een biosensor voor het meten van extracellulaire waterstofperoxideconcentraties Studie van olifant, capibara, mensenhaar vindt dat dikker haar niet altijd sterker is
Studie van olifant, capibara, mensenhaar vindt dat dikker haar niet altijd sterker is
Hoofdlijnen
- Hoe de gecorrigeerde WBC-telling te berekenen
- GMO-experimenten
- De verpakking van DNA in chromosomen
- Houden mannelijke vissen ze liever groot en kleurrijk?
- Beschrijving van gen-splitsing als een DNA-techniek
- Vissers in Istanbul houden traditie in stand ondanks voorraadalarm
- Hoe moleculaire scharen ziekten kunnen oplossen en DNA kunnen bewerken
- Oorsmeer zoals ijskernen - ontsluiten het verleden verborgen in oordopjes voor walvissen
- Het weer in november is een lastige tijd voor schildpadden
 Kom samen:Nieuwe lasertechniek bindt aluminium met kunststof bij spuitgieten
Kom samen:Nieuwe lasertechniek bindt aluminium met kunststof bij spuitgieten Een betere toekomst voor LED's:NIST introduceert nieuw laboratorium voor lampkalibratie
Een betere toekomst voor LED's:NIST introduceert nieuw laboratorium voor lampkalibratie De laatste lockdown had minder impact op de luchtvervuilingsniveaus in het VK dan de eerste, nieuwe analyse toont
De laatste lockdown had minder impact op de luchtvervuilingsniveaus in het VK dan de eerste, nieuwe analyse toont Een EMF-detector bouwen
Een EMF-detector bouwen  De ecologische kosten van oorlog:conflict een consequente moordenaar van Afrikaanse megafauna
De ecologische kosten van oorlog:conflict een consequente moordenaar van Afrikaanse megafauna Anonieme hackers richten zich op Spaanse sites in protest in Catalonië
Anonieme hackers richten zich op Spaanse sites in protest in Catalonië Stijgende overstromingsverzekeringskosten en toenemende lasten voor gemeenschappen en huiseigenaren in New York City
Stijgende overstromingsverzekeringskosten en toenemende lasten voor gemeenschappen en huiseigenaren in New York City Hoe krijg ik een deeltjesdetector in een vliegtuig?
Hoe krijg ik een deeltjesdetector in een vliegtuig?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com