
Wetenschap
Wazige beeldlimieten verduidelijkt dankzij informatietechnologie
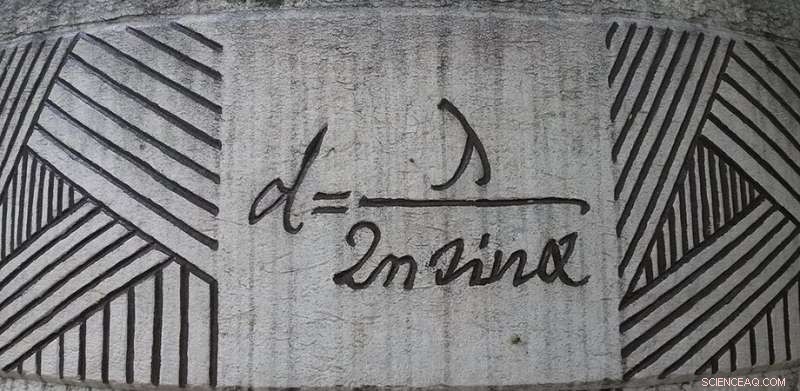
Ernst Abbe's diffractievergelijking te zien in Jena, Duitsland. Krediet:Daniel Mietchen, Wikimedia, commons.wikimedia.org/wiki/File:Ernst-Abbe-Denkmal_Jena_F%C3%BCrstengraben_-_20140802_125709.jpg
Hoewel ons is verteld dat een foto meer zegt dan duizend woorden, dat cliché onderschat serieus de waarde van een goed imago. Ons begrip van hoe de wereld werkt, wordt vereenvoudigd door ons vermogen om gegevens in afbeeldingen om te zetten. Beeldvorming vormt de kern van de wetenschap:als het kan worden gemeten, het zal worden omgezet in een te analyseren afbeelding.
De beperkende factor van beeldvorming is resolutie. Hoe dichtbij kunnen twee objecten zijn voordat een beeldvormingssysteem ze reduceert tot een enkele wazige plek? Die vraag werd aanvankelijk beantwoord door Ernst Abbe in 1873. Hij theoretiseerde dat als twee objecten dichterbij zijn dan ongeveer een halve golflengte, ze kunnen niet worden opgelost. Abbe bereikte zijn limiet door te bedenken hoe diffractie door een lens een puntbron zou vervagen.
Ongeveer een eeuw lang, Abbe's diffractielimiet werd als een wetenschappelijke waarheid beschouwd. Zeker wel, je zou wat spelletjes kunnen spelen met het verlichtende licht en het beeldmedium om een factor twee of drie te krijgen, maar factoren van tien of 100 waren ondenkbaar. Dat is nu veranderd, met veel beeldvormingstechnieken die de diffractielimiet van Abbe kunnen overschrijden, die nu verbrijzeld ligt in de hoek van de werkplaats van de wetenschap onder de schaduw van twee Nobelprijzen. Maar is er nog een limiet? Hoe dichtbij kunnen twee objecten zijn voordat ze vervagen tot een enkele plek? Dit is de vraag die Evgenii Narimanov van de Purdue University in een recent onderzoek heeft proberen te beantwoorden Geavanceerde fotonica papier.
Vervaging van beeldvorming
Als het gaat om beeldvorming, het is een stuk eenvoudiger om het concept van diffractie opzij te zetten en in plaats daarvan over informatie te denken. Wanneer een object wordt afgebeeld, licht wordt door het object naar het beeldvormingssysteem verstrooid. Het ruimtelijke patroon, of informatie, van het beeld wordt gedragen door de ruimtelijke frequenties van het licht. Om een nauwkeurig beeld te herstellen, het beeldvormingssysteem moet die ruimtelijke frequenties uitzenden zonder ze te wijzigen. Maar, elk systeem heeft zijn grenzen, dus de bijdrage van sommige ruimtelijke frequenties zal verloren gaan.
Het resulterende beeld wordt gemaakt door de ruimtelijke frequenties die door het beeldvormingssysteem worden uitgezonden, opnieuw te combineren. Als het beeldvormingssysteem geen frequenties boven een bepaalde limiet kan verzenden, dan bevat de afbeelding die informatie niet, met vervaging tot gevolg. Als je van mening bent dat het beeldvormingssysteem ruimtelijke frequenties kan verzenden tot aan een afsnijfrequentie, maar niet in staat om frequenties boven de grenswaarde uit te zenden, dan zal de resulterende beeldresolutie precies zijn zoals voorspeld door Abbe (maar met eenvoudigere wiskunde).
Inderdaad, de informatie die door een beeldvormingssysteem wordt verzonden, wordt beschreven door precies dezelfde wiskunde als die wordt gebruikt door ingenieurs die de overdracht van gegevens via telefoondraden bestuderen, waarmee de instrumenten van de informatietheorie kunnen worden gebruikt om de prestaties van beeldvormingssystemen te voorspellen.
De berichten in een afbeelding decoderen
Narimanov is een stap verder gegaan in het abstraheren van het beeldvormingsproces door alleen rekening te houden met informatieoverdracht, onafhankelijk van hoe die informatie is gecodeerd. Wanneer dat gedaan is, de resolutie van een afbeelding wordt alleen bepaald door de wederzijdse informatie die wordt gedeeld tussen het object en de afbeelding. In dit kader is die onafhankelijk is van alle functionele details, de resolutielimiet wordt bepaald door de ruis die wordt geïntroduceerd tijdens de informatieoverdracht. In de praktijk wordt de ruis veroorzaakt door de detector, lichtverstrooiing, schommelingen in de verlichtingsomstandigheden, en nog veel meer details.
Door deze abstracte benadering te volgen, Narimanov was in staat om een theorie te produceren die de best mogelijke resolutie voor een afbeelding voorspelt, alleen gebaseerd op de verhouding tussen de sterkte van het signaal en de hoeveelheid ruis. Hoe hoger de signaal-ruisverhouding, hoe beter de mogelijke resolutie.
Door gebruik te maken van deze theorie, het document bevat ook een aantal berekeningen voor meer specifieke beeldvormingssystemen, zoals diegene die gestructureerde verlichting gebruiken, en in het geval van het afbeelden van schaarse objecten, die weinig functies hebben die vaak samengeklonterd zijn. Ook de mogelijkheden voor het verbeteren van een beeld met nabewerking komen aan bod:we kennen allemaal de televisiemisdaaddrama's die beelden naar believen kunnen verbeteren. Hoewel dit niet mogelijk is zoals op tv wordt getoond, er zit een kern van waarheid in. Geldige methoden voor het computationeel nabewerken van een afbeelding kunnen enkele verborgen details onthullen. Deze theorie laat de grenzen van die benadering zien, te.
De aanpak van Narimanov onthult niet welk aspect van een systeem momenteel de resolutie beperkt. Daarom, er zijn nog meer specifieke modellen nodig. In plaats daarvan, het is beter om het model van Narimanov als een gids te beschouwen:waar is de grootste winst in resolutie te vinden voor de minste inspanning? Die informatie is nuttig bij het beslissen waar u tijd en geld in wilt steken.
 Een RNA-sleutel die de aangeboren immuniteit ontgrendelt
Een RNA-sleutel die de aangeboren immuniteit ontgrendelt Functionele films gemaakt van milieuvriendelijke kleimineralen en kleurstoffen
Functionele films gemaakt van milieuvriendelijke kleimineralen en kleurstoffen Wat is de rol van carotenoïden in fotosynthese?
Wat is de rol van carotenoïden in fotosynthese?  Aan het oppervlak blootgestelde nanodendrieten met hoge index als ORR-elektrokatalysator
Aan het oppervlak blootgestelde nanodendrieten met hoge index als ORR-elektrokatalysator Chemici synthetiseren voor het eerst perseanol
Chemici synthetiseren voor het eerst perseanol
 Waarom het verhogen van de productie van schaliegas de uitstoot van broeikasgassen niet zal verminderen?
Waarom het verhogen van de productie van schaliegas de uitstoot van broeikasgassen niet zal verminderen? Hoe spinnen te identificeren in Alberta
Hoe spinnen te identificeren in Alberta Licht werpen op hoe stedelijk vuil de chemische reacties in steden beïnvloedt
Licht werpen op hoe stedelijk vuil de chemische reacties in steden beïnvloedt Onderzoeksprojecties tonen aan dat klimaatverandering het commerciële energieverbruik van Indiana verhoogt, woongebruik verminderen
Onderzoeksprojecties tonen aan dat klimaatverandering het commerciële energieverbruik van Indiana verhoogt, woongebruik verminderen Eeuwig stinkende stad? De afvalcrisis in Rome wekt gezondheidsangst op
Eeuwig stinkende stad? De afvalcrisis in Rome wekt gezondheidsangst op
Hoofdlijnen
- Beschrijving van de basisfuncties van enzymen in cellen
- Hoe een cel te splitsen in Two
- Diepe wortels in planten aangedreven door bodemhydrologie
- Hoe is het schrijven geëvolueerd?
- Analyse van oud DNA onthult een voorheen niet-herkend geslacht van uitgestorven paarden dat ooit door Noord-Amerika zwierf
- Verschillen tussen lichaamscellen en neuronen
- Cell Analogy Project Ideas
- De structuur en functie van mRNA
- Team ontdekt nieuwe mechanismen voor DNA-stabiliteit
- Een unieke scanning tunneling microscoop met magnetische koeling om kwantumeffecten te bestuderen

- Niezen bewakers kunnen vliegtuigen met volledige capaciteit veiliger maken tegen verspreiding van COVID-19
- Hawking, de man wiens hersenen de handicap overstegen

- Natuurkundigen vinden bewijs van voorheen onzichtbare overgang in ferro-elektriciteit

- Fotonische doping maakt klasse van metamaterialen gemakkelijker te fabriceren

 NASA's MAVEN blijft de inspanningen van Mars op het gebied van wetenschap en telecommunicatie bevorderen
NASA's MAVEN blijft de inspanningen van Mars op het gebied van wetenschap en telecommunicatie bevorderen De zwarte doos van geautomatiseerde machine learning openbreken
De zwarte doos van geautomatiseerde machine learning openbreken Nieuw materiaal kan leiden tot uitwisbare en herschrijfbare optische chips
Nieuw materiaal kan leiden tot uitwisbare en herschrijfbare optische chips Boeing verwacht dat Max-jet pas in de zomer wordt vrijgegeven
Boeing verwacht dat Max-jet pas in de zomer wordt vrijgegeven IJs in Ceres beschaduwde kraters die verband houden met kantelgeschiedenis
IJs in Ceres beschaduwde kraters die verband houden met kantelgeschiedenis Onderzoek bevordert de duurzaamheid van de productie van chirurgische latexhandschoenen
Onderzoek bevordert de duurzaamheid van de productie van chirurgische latexhandschoenen Studie roept op tot juridische hervorming van verborgen misdaad waar maar weinig mannelijke slachtoffers over zullen praten
Studie roept op tot juridische hervorming van verborgen misdaad waar maar weinig mannelijke slachtoffers over zullen praten Muziekhitlijsten zijn steeds meer van korte duur
Muziekhitlijsten zijn steeds meer van korte duur
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

