
Wetenschap
Bestelling verborgen in wanorde

Hoe ongeordend een systeem in eerste instantie ook mag zijn - individuele optimalisatie van elke cel resulteert geleidelijk in de vorming van dezelfde structuur met een verborgen volgorde. Krediet:Michael A. Klatt
Het opdelen van ruimte in cellen met optimale geometrische eigenschappen is een centrale uitdaging op veel gebieden van wetenschap en technologie. Onderzoekers van het Karlsruhe Institute of Technology (KIT) en collega's uit verschillende landen hebben nu ontdekt dat in amorfe, d.w.z. wanordelijk, systemen, optimalisatie van de individuele cellen resulteert geleidelijk in dezelfde structuur, hoewel het amorf blijft. De wanordelijke structuur convergeert snel naar hyperuniformiteit, een verborgen orde op grote schaal. Dit wordt gemeld in Natuurcommunicatie .
Bij wetenschappelijk onderzoek wordt vaak gezocht naar een optimaal schuim of naar een methode om bollen zo dicht mogelijk te verpakken. De ideale mozaïekpatroon van driedimensionale ruimte is lange tijd bestudeerd door wetenschappers. Het is niet alleen van theoretisch belang, maar relevant voor veel praktische toepassingen, onder meer voor telecommunicatie, afbeelding verwerken, of complexe korrels. Onderzoekers van KIT's Institute of Stochastics hebben nu een speciaal probleem van mozaïekpatroon bestudeerd, het kwantisatorprobleem. "Het doel is om de ruimte in cellen te verdelen, en alle punten in een cel zo dicht mogelijk bij het celcentrum, intuïtief gesproken, " zegt dr. Michael Andreas Klatt, voormalig medewerker van het Instituut, die nu aan de Princeton University in de VS werkt. Oplossingen van het quantizer-probleem kunnen worden gebruikt voor de ontwikkeling van nieuwe materialen en kunnen in de toekomst bijdragen aan een beter begrip van de unieke eigenschappen van complex celweefsel.
Het theoretische werk combineert methoden van stochastische meetkunde en statistische fysica, en wordt nu gerapporteerd in Natuurcommunicatie . De onderzoekers van het KIT, Princeton Universiteit, Friedrich-Alexander-Universität (FAU) Erlangen-Neurenberg, Ruđer Bošković Instituut in Zagreb, en Murdoch University in Perth gebruikten het zogenaamde Lloyd-algoritme, een methode om ruimte in uniforme gebieden te verdelen. Elke regio heeft precies één centrum en bevat die punten in de ruimte die dichter bij dit centrum liggen dan bij enig ander centrum. Dergelijke gebieden worden Voronoi-cellen genoemd. Het Voronoi-diagram bestaat uit alle punten met meer dan één dichtstbijzijnde middelpunt en, Vandaar, die de grenzen van de regio's vormen.
De wetenschappers bestudeerden stapsgewijze lokale optimalisatie van verschillende puntpatronen en ontdekten dat ze allemaal volledig amorf, d.w.z. wanordelijk, toestanden blijven niet alleen volledig amorf, maar dat de aanvankelijk diverse processen samenkomen tot een statistisch niet te onderscheiden ensemble. Stapsgewijze lokale optimalisatie compenseert ook snel extreme globale fluctuaties van dichtheid. "De resulterende structuur is bijna hyperuniform. Het vertoont geen duidelijke, maar een verborgen orde op grote schaal, ' zegt Klat.
Vandaar, deze volgorde verborgen in amorfe systemen is universeel, d.w.z. stabiel en onafhankelijk van eigenschappen van de begintoestand. Dit geeft basisinzicht in de interactie van orde en wanorde en kan onder meer worden gebruikt voor de ontwikkeling van nieuwe materialen. Van bijzonder belang zijn fotonische metamaterialen vergelijkbaar met een halfgeleider voor licht of zogenaamde blokcopolymeren, d.w.z. nanodeeltjes die zijn samengesteld uit langere sequenties of blokken van verschillende moleculen die op een zelfgeorganiseerde manier regelmatige en complexe structuren vormen.
 Doorbraak in onderzoek naar schone diesel
Doorbraak in onderzoek naar schone diesel Een mooie plant van de zomer produceert een veelbelovende anti-diabetes verbinding
Een mooie plant van de zomer produceert een veelbelovende anti-diabetes verbinding Een doorbraak in onderzoek naar chirale polymere dunne films zou een nieuwe generatie apparaten mogelijk kunnen maken
Een doorbraak in onderzoek naar chirale polymere dunne films zou een nieuwe generatie apparaten mogelijk kunnen maken Geurafgevende stof kan zweterige gymkleding helpen neutraliseren
Geurafgevende stof kan zweterige gymkleding helpen neutraliseren Polymeeronderzoekers ontdekken pad naar duurzame en biologisch afbreekbare polyesters
Polymeeronderzoekers ontdekken pad naar duurzame en biologisch afbreekbare polyesters
 Wat zit er onder de Antarctische ijskap?
Wat zit er onder de Antarctische ijskap? Groener brood bakken na COVID
Groener brood bakken na COVID Na Harvey:Wetenschappers bestuderen veranderingen in Galveston Bay
Na Harvey:Wetenschappers bestuderen veranderingen in Galveston Bay Grijp het moment:mensen willen de natuur helpen na de bosbranden
Grijp het moment:mensen willen de natuur helpen na de bosbranden Wat met roet bedekt, Honderd jaar oude vogels kunnen ons vertellen over het redden van het milieu
Wat met roet bedekt, Honderd jaar oude vogels kunnen ons vertellen over het redden van het milieu
Hoofdlijnen
- De nadelen van gelelektroforese
- Alles-in-één reparatiekit maakt CRISPR-genbewerking nauwkeuriger
- Nieuwe vissoorten vertonen opvallend kleurverschil tussen mannetjes en vrouwtjes
- Florida probeert het tij te keren bij de invasie van leguaan
- GMO-experimenten
- Trucs voor het onthouden van dierenfylum
- Arctisch, grote visserslanden zijn het erover eens dat er niet gevist wordt in het noordpoolgebied, voor nu
- Staan we aan het begin van het einde van de westerse beschaving?
- Wat is de Chromatins-functie?
- Huishoudfenomeen waargenomen door Leonardo da Vinci eindelijk uitgelegd

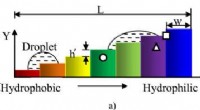
- Zelfs druppeltjes gaan soms de trap op
- Klein, injecteerbare sensoren kunnen de hersenactiviteit volgen zonder chirurgie of implantaten

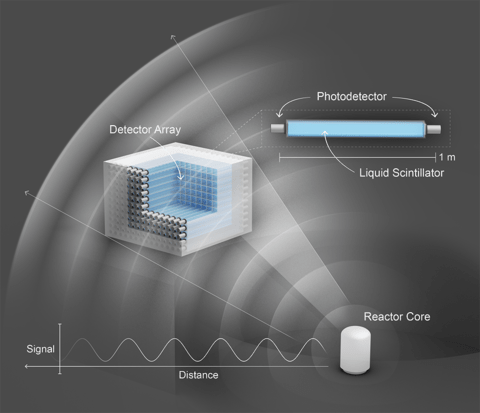
- Op zoek naar steriele neutrino's
- Spectrale verhulling kan objecten onzichtbaar maken onder realistische omstandigheden

 muren versterken, levens redden
muren versterken, levens redden Historische films kunnen dankzij het azijnsyndroom veel sneller vergaan dan we dachten
Historische films kunnen dankzij het azijnsyndroom veel sneller vergaan dan we dachten Komeet 2019 LD2 (ATLAS) blijkt actief in transitie te zijn
Komeet 2019 LD2 (ATLAS) blijkt actief in transitie te zijn Vraag en antwoord:impact van inspanningen om ontbossing in Amazone te verminderen overschat, studie vondsten
Vraag en antwoord:impact van inspanningen om ontbossing in Amazone te verminderen overschat, studie vondsten Hoe krijgen mensen stikstof in hun lichaam?
Hoe krijgen mensen stikstof in hun lichaam?  Waarom zijn recordregens in Japan zo dodelijk?
Waarom zijn recordregens in Japan zo dodelijk? Saturnusmaan Titan heeft aardachtige kenmerken
Saturnusmaan Titan heeft aardachtige kenmerken Nieuwe soort kleine tyrannosaurus voorspelt opkomst van T. rex
Nieuwe soort kleine tyrannosaurus voorspelt opkomst van T. rex
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

