
Wetenschap
De wetenschap van het breien, niet geplukt

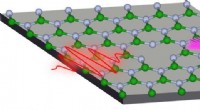
a) Breien is een periodieke structuur van schuifknopen. b) Textiel met ingewikkelde patronen wordt gebreid door schuifknopen in specifieke combinaties te combineren. Krediet:Elisabetta Matsumoto
Meer dan 3 dateren, 000 jaar, breien is een oude vorm van vervaardigen, maar Elisabetta Matsumoto van het Georgia Institute of Technology in Atlanta gelooft dat het van onschatbare waarde zal zijn om te begrijpen hoe steektypes vorm en rekbaarheid bepalen voor het ontwerpen van nieuwe "afstembare" materialen. Bijvoorbeeld, weefselachtig flexibel materiaal zou kunnen worden vervaardigd om biologische weefsels te vervangen, zoals gescheurde banden, met rekbaarheid en gepersonaliseerde maatvoering voor elk individu.
Tijdens de American Physical Society March Meeting in Boston deze week, Matsumoto zal haar werk presenteren over de wiskundige regels die ten grondslag liggen aan breien. Ze zal ook deelnemen aan een persconferentie waarin het werk wordt beschreven. Informatie over inloggen om op afstand mee te kijken en vragen te stellen vindt u aan het einde van dit persbericht.
"Door een steek te kiezen, kiest u niet alleen de geometrie, maar ook de elastische eigenschappen, en dat betekent dat u de juiste mechanische eigenschappen kunt inbouwen voor alles van lucht- en ruimtevaarttechniek tot weefselsteigermaterialen, ’ zei Matatsumoto.
Matsumoto genoot als kind van breien en toen ze later geïnteresseerd raakte in wiskunde en natuurkunde, ze ontwikkelde een nieuwe waardering voor haar hobby.
"Ik realiseerde me dat er gewoon een enorme hoeveelheid wiskunde en materiaalwetenschap in textiel zit, maar dat wordt heel erg vanzelfsprekend gevonden, ’ zei Matatsumoto.
"Elk type steek heeft een andere elasticiteit, en als we al het mogelijke uitzoeken, kunnen we dingen maken die op een bepaalde plaats stijf zijn met een bepaald type steek, en gebruik een ander type steek op een andere plaats om andere functionaliteit te krijgen."

Topologische defecten in het vierkant kunnen de (a) out-of-plane en (b) in-plane vervormingen van gebreid textiel vormen. Krediet:Elisabetta Matsumoto
Leden van de Matsumoto-groep beginnen zich te verdiepen in de complexe wiskunde die de mechanische eigenschappen codeert binnen de in elkaar grijpende reeks schuifknopen van een materiaal. Maar het toepassen van de pure wiskunde van de knooptheorie op de enorme catalogus van breipatronen is een lastig proces voor Matsumoto's afgestudeerde student, Shashank Markande.
"Steken hebben een aantal zeer vreemde beperkingen, bijvoorbeeld, Ik moet het kunnen maken met twee naalden en één stuk garen - hoe vertaal je dat in wiskunde?" zei Matsumoto.
Maar Markande begint de gebreide algebra in grotere, complexere patronen, en hij voert dit in de elastische modellering van eenvoudige roosterachtige breisels, die Matsumoto's postdoc, Michael Dimitriyev ontwikkelt zich.
Dimitriyev's code voor het oplossen van stofgedrag toont potentieel dat verder gaat dan materiaalontwerp, op het gebied van grafische computerspelletjes.

Vijf stoffen (a) tricotsteek, (b) omgekeerde tricotsteek, (c) kousenband, (d) 1x1 ribbels en (e) zaad gemaakt van breisels en averecht. Elk van deze is dubbel periodiek - met eenheidscel omlijnd door een stippellijn. Krediet:Elisabetta Matsumoto
"Stof en stof zien er in computerspellen een beetje vreemd uit, omdat ze gebruik maken van eenvoudige kralen- en veerelasticiteitsmodellen, dus als we een simpele opstelling van differentiaalvergelijkingen kunnen bedenken, kan het helpen om dingen er beter uit te laten zien, ’ zei Matatsumoto.
Op dit moment, de Matsumoto-groep richt zich op zeer eenvoudige steekpatronen en rondingen in gebreide roosters; echter, binnenkort hopen ze te begrijpen hoe breisels zich in 3D gedragen.
Maar terwijl ze de wiskunde tussen de steken uitpluizen, Matsumoto zorgt ervoor dat ze in de gaten houden hoe deze patronen samenkomen door af en toe een knutselsessie te organiseren met de origami-groep naast de deur.
 Nieuwe familie in de buurt:een nieuwe groep glycosidische enzymen
Nieuwe familie in de buurt:een nieuwe groep glycosidische enzymen Onderzoek naar kant-en-klare therapeutische voeding streeft naar drastische vermindering van sterfgevallen door ernstige acute ondervoeding
Onderzoek naar kant-en-klare therapeutische voeding streeft naar drastische vermindering van sterfgevallen door ernstige acute ondervoeding Hoe te converteren van mol per liter naar percentage
Hoe te converteren van mol per liter naar percentage  Duurzame chemie op kwantumniveau
Duurzame chemie op kwantumniveau Een zwaargewicht oplossing voor lichtere gevechtsvoertuigen
Een zwaargewicht oplossing voor lichtere gevechtsvoertuigen
 Newsom lanceert inspanningen om de droogte in Californië aan te pakken; noodgevallen verklaard in 2 provincies
Newsom lanceert inspanningen om de droogte in Californië aan te pakken; noodgevallen verklaard in 2 provincies Amerikanen zeggen dat ze zich zorgen maken over klimaatverandering - dus waarom stemmen ze niet op die manier?
Amerikanen zeggen dat ze zich zorgen maken over klimaatverandering - dus waarom stemmen ze niet op die manier? Wat gebeurt er als er regen valt op woestijnbodems? Een bijgewerkt model biedt antwoorden
Wat gebeurt er als er regen valt op woestijnbodems? Een bijgewerkt model biedt antwoorden Hoe maak je een barometer met minerale olie
Hoe maak je een barometer met minerale olie  Piek in radioactiviteit in de lucht gedetecteerd in Europa
Piek in radioactiviteit in de lucht gedetecteerd in Europa
Hoofdlijnen
- Wetenschappers onderzoeken mysteries achter diversiteit van DNA-samenstelling tussen soorten
- De wilde ezel keert terug
- Koud verbijsterde zeekoeien, zeeschildpadden opwarmen bij SeaWorld
- Hoe de cellen van planten, dieren en eencellige organismen te vergelijken
- Chimerisme:je kunt je eigen tweeling zijn
- Hoe slapende listeria zich in cellen verbergt
- Wat is mRNA, rRNA en tRNA?
- Ongedierteresistentie tegen biotech-gewassen stijgt
- Kankerwetenschappers ruiken de genen achter Durians Famous Stink
- Nieuw quantumtransmissieprotocol heeft een hogere datatransmissiesnelheid, robuustheid tegen interferentie

- Wetenschappers werpen licht op het degradatiemechanisme van halfgeleiders

- Eerste waarneming van mysterieus Majorana-fermion op een gewoon metaal

- Een stap in de richting van het beheersen van spin-afhankelijke petahertz-elektronica door materiaaldefecten
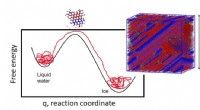
- Hoe ijs in wolken wordt geboren
 Het delen van gegevens van de University of Chicago Medical Centers met Google brengt de privacy van patiënten in gevaar, rechtszaak beweert
Het delen van gegevens van de University of Chicago Medical Centers met Google brengt de privacy van patiënten in gevaar, rechtszaak beweert Verbeterde versterkertechnologie voor gebruik in positronemissietomografie
Verbeterde versterkertechnologie voor gebruik in positronemissietomografie Onderzoek identificeert een andere verklaring voor de huwelijkspremie voor nakomelingen
Onderzoek identificeert een andere verklaring voor de huwelijkspremie voor nakomelingen Wetenschappers in DR Congo doen onderzoek ondanks conflict armoede
Wetenschappers in DR Congo doen onderzoek ondanks conflict armoede Nieuwe methode verbetert de nauwkeurigheid van beeldvormingssystemen
Nieuwe methode verbetert de nauwkeurigheid van beeldvormingssystemen Schatz Barometer-instructies
Schatz Barometer-instructies  Hoe gedraag je je in een dierentuin - volgens de wetenschap
Hoe gedraag je je in een dierentuin - volgens de wetenschap Simjacker-exploit is onafhankelijk van het type handset, maakt gebruik van sms-aanval
Simjacker-exploit is onafhankelijk van het type handset, maakt gebruik van sms-aanval
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Portuguese | Swedish | German | Dutch | Danish | Norway | Spanish |

-
Wetenschap © https://nl.scienceaq.com

