
Wetenschap
Amoeba vindt benaderende oplossingen voor NP-hard probleem in lineaire tijd
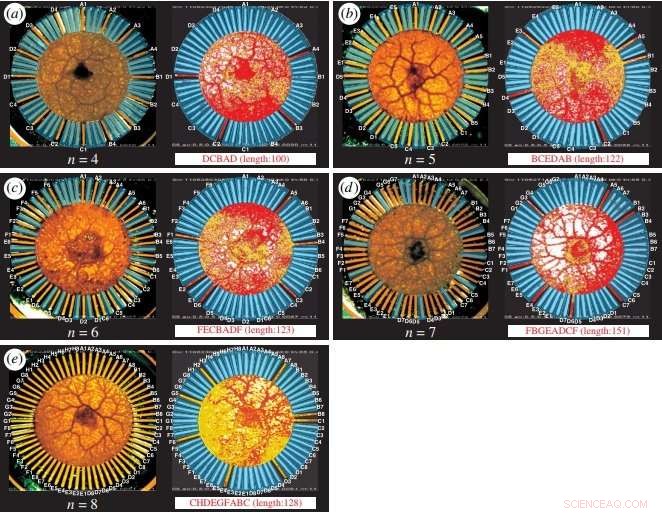
TSP-oplossingen verkregen door het op amoeben gebaseerde computersysteem voor 4, 5, 6, 7, en 8 steden. Krediet:Zhu et al. ©2018 Royal Society Open Science
Onderzoekers hebben aangetoond dat een amoebe - een eencellig organisme dat voornamelijk bestaat uit gelatineus protoplasma - unieke computervaardigheden heeft die op een dag een concurrerend alternatief kunnen bieden voor de methoden die door conventionele computers worden gebruikt.
De onderzoekers, geleid door Masashi Aono aan de Keio University, een amoebe toegewezen om het Travelling Salesman Problem (TSP) op te lossen. De TSP is een optimalisatieprobleem waarbij het doel is om de kortste route tussen verschillende steden te vinden, zodat elke stad precies één keer wordt bezocht, en het begin- en eindpunt zijn hetzelfde.
Het probleem is NP-moeilijk, wat betekent dat naarmate het aantal steden toeneemt, de tijd die een computer nodig heeft om het op te lossen groeit exponentieel. De complexiteit is te wijten aan het grote aantal mogelijke oplossingen. Bijvoorbeeld, voor vier steden, er zijn slechts drie mogelijke routes. Maar voor acht steden, het aantal mogelijke routes stijgt tot 2520.
In de nieuwe studie de onderzoekers ontdekten dat een amoebe redelijke (bijna optimale) oplossingen voor de TSP kan vinden in een tijd die alleen lineair groeit naarmate het aantal steden toeneemt van vier naar acht. Hoewel conventionele computers ook benaderende oplossingen kunnen vinden in lineaire tijd, de benadering van de amoebe is compleet anders dan traditionele algoritmen. Zoals de wetenschappers uitleggen, de amoebe verkent de oplossingsruimte door de gel continu met een constante snelheid te herverdelen in zijn amorfe lichaam, en door optische feedback parallel te verwerken in plaats van serieel.
Hoewel een conventionele computer de TSP nog steeds veel sneller kan oplossen dan een amoebe, vooral voor kleine probleemgroottes, de nieuwe resultaten zijn intrigerend en kunnen leiden tot de ontwikkeling van nieuwe analoge computers die benaderende oplossingen afleiden van computationeel complexe problemen van veel grotere omvang in lineaire tijd.
Hoe het werkt
Het specifieke type amoebe dat de wetenschappers gebruikten was een plasmodium of "echte slijmzwam, " die ongeveer 12 mg weegt en havervlokken verbruikt. Deze amoebe vervormt voortdurend zijn amorfe lichaam door herhaaldelijk gel toe te voeren en te verwijderen met een snelheid van ongeveer 1 mm / seconde om pseudopod-achtige aanhangsels te creëren.
In hun experimenten, de onderzoekers plaatsten de amoebe in het midden van een stervormige chip, dat is een ronde plaat met 64 smalle kanalen die naar buiten uitsteken, en plaatste de chip vervolgens op een agarplaat. De amoebe zit opgesloten in de chip, maar kan nog steeds naar de 64 kanalen gaan.
Om de opname van voedingsstoffen te maximaliseren, de amoebe probeert uit te zetten in de chip om in contact te komen met zoveel mogelijk agar. Echter, de amoebe houdt niet van licht. Aangezien elk kanaal selectief door licht kan worden verlicht, het is mogelijk om de amoebe te dwingen zich terug te trekken uit de verlichte kanalen.
Om de TSP te modelleren, elk kanaal in de stellate-chip vertegenwoordigt een geordende stad in de route van de verkoper. Bijvoorbeeld, in het geval met vier steden met het label A-D, als de amoebe de kanalen A4 bezet, B2, C1, en D3, dan is de corresponderende oplossing voor de TSP C, B, NS, EEN, C.
Om de amoebe naar een optimale of bijna optimale oplossing te leiden, de sleutel ligt in het regelen van het licht. Om dit te doen, de onderzoekers gebruiken een neuraal netwerkmodel waarbij het systeem elke zes seconden update welke kanalen verlicht zijn. Het model bevat informatie over de afstand tussen elk paar steden, evenals feedback van de huidige positie van de amoebe in de kanalen.
Het model zorgt ervoor dat de amoebe op een aantal manieren een geldige oplossing voor de TSP vindt. Bijvoorbeeld, zodra de amoebe een bepaald deel van een bepaald kanaal heeft ingenomen, zeg A3, dan kanalen A1, A2, en alle andere "A"-kanalen worden verlicht om te voorkomen dat stad A twee keer wordt bezocht. Ook, B3, C3, D3, en alle andere "3"-kanalen zijn verlicht om gelijktijdige bezoeken aan meerdere steden te verbieden.
Het model houdt rekening met de afstanden tussen steden door het gemakkelijker te maken om kanalen te verlichten die steden met grotere afstanden vertegenwoordigen dan met kortere afstanden. Bijvoorbeeld, stel dat de amoebe kanaal B2 bezet, en is begonnen de kanalen C3 en D3 in gelijke hoeveelheden binnen te dringen, en de afstand tussen steden B en C is 100, terwijl de afstand tussen steden B en D 50 is. De grotere afstand tussen B en C zorgt er uiteindelijk voor dat het systeem kanaal C3 verlicht, waardoor de amoebe zich terugtrekt uit dat kanaal, maar hem in staat stelt verder te gaan naar D3.
Algemeen, het modelleren van de TSP met een amoebe maakt gebruik van de natuurlijke neiging van de amoebe om een stabiel evenwicht te zoeken. Omdat kanalen die kortere routes vertegenwoordigen minder snel worden verlicht, de amoebe kan zich in die kanalen verspreiden en andere niet-verlichte kanalen blijven verkennen om het oppervlak op de agarplaat te maximaliseren.
De onderzoekers ontwikkelden ook een computersimulatie genaamd AmoebaTSP die enkele van de belangrijkste kenmerken nabootst van hoe de amoebe het probleem aanpakt, inclusief de continue beweging van gel, aangezien deze met een constante snelheid wordt toegevoerd en uit verschillende kanalen wordt onttrokken.
"In onze sterchip voor het oplossen van de N -stad TSP, de totale oppervlakte van het lichaam van de amoebe wordt N wanneer de amoebe eindelijk een benaderende oplossing vindt, "Aono vertelde" Phys.org . "Er lijkt een 'wet' te zijn dat de amoebe zijn gelatineuze hulpbron levert om met een constante snelheid uit te breiden in de niet-verlichte kanalen, zeggen, x . Deze wet zou worden gehandhaafd, zelfs als sommige bronnen terugkaatsen van verlichte kanalen. Dan is de tijd die nodig is om het lichaamsgebied uit te breiden N om de oplossing te vertegenwoordigen wordt N / x . Dit mechanisme zou de oorsprong zijn van de lineaire tijd, en het werd gereproduceerd door ons computersimulatiemodel.
"Maar nog steeds, het mechanisme waarmee de amoebe de kwaliteit van de benaderde oplossing handhaaft, dat is, de korte routelengte, blijft een mysterie. Het lijkt erop dat ruimtelijk en temporeel gecorreleerde bewegingen van de vertakte delen van de amoebe die zich op verre kanalen bevinden, de sleutel zijn. Elk van deze takken oscilleert zijn volume met een tijdelijk 'geheugen' aan verlichte ervaringen. Groepen van de takken voeren synchronisatie en desynchronisatie uit om informatie te delen, ook al zijn ze ruimtelijk ver weg."
In de toekomst, de onderzoekers zijn van plan om de computercapaciteiten van de amoebe verder te verbeteren.
"We zullen verder onderzoeken hoe deze complexe spatiotemporele oscillerende dynamiek de rekenprestaties verbetert bij het vinden van oplossingen van hogere kwaliteit in kortere tijd, " zei co-auteur Song-Ju Kim van de Keio University. "Als het kan worden verduidelijkt, de kennis zal bijdragen aan het creëren van nieuwe analoge computers die gebruik maken van de spatiotemporele dynamiek van elektrische stroom in zijn circuit.
"Natuurlijk, enkele andere algoritmen draaien op traditionele digitale computers voor lineaire tijd, we kunnen benaderende oplossingen voor TSP afleiden. Anderzijds, bij het uitvoeren van onze simulatiemodellen (AmoebaTSP of zijn ontwikkelde versies) op de traditionele computers zoals we deden in deze studie, de analoge en parallelle spatiotemporele dynamiek vereisen niet-lineaire tijd om ze te simuleren als digitale en seriële processen. We proberen dus oplossingen van veel hogere kwaliteit te verkrijgen dan de oplossingen die zijn afgeleid van de traditionele door onze modellen lineair of korter op de analoge computers te laten draaien."
De onderzoekers verwachten ook dat, door een grotere chip te fabriceren, de amoebe zal TSP-problemen met honderden steden kunnen oplossen, hoewel dit tienduizenden kanalen zou vereisen.
© 2018 Wetenschap X Netwerk
 Na de aardbeving tussen Iran en Irak, seismologen werken aan het invullen van de foutenkaart van de regio
Na de aardbeving tussen Iran en Irak, seismologen werken aan het invullen van de foutenkaart van de regio Methaanemissies detecteren tijdens COVID-19
Methaanemissies detecteren tijdens COVID-19 Eastern Caribbean geeft zeldzame waarschuwingen voor rommelende vulkanen
Eastern Caribbean geeft zeldzame waarschuwingen voor rommelende vulkanen Wetenschappers publiceren studie over glaciale koolstofcyclus
Wetenschappers publiceren studie over glaciale koolstofcyclus Tumorvrije bot:onderzoek onderstreept de wedergeboorte van Boston Harbor
Tumorvrije bot:onderzoek onderstreept de wedergeboorte van Boston Harbor
Hoofdlijnen
- Hoe het Human Microbiome-project werkt
- Studie belicht de instandhoudingsbehoeften van recent ontdekte vissoorten in Southwest Virginia
- Recordaantal walvissen geteld in Patagonië in Argentinië
- Nieuwe ontdekking daagt lang gekoesterde evolutietheorie uit
- Wat is het laatste nieuws over de darmflora? Concordia-studenten microbiologie publiceren hun bevindingen
- Nieuwe antibioticaresistentiegenen gevonden
- Wat zit er aan de linkerkant van je lichaam in de menselijke anatomie?
- Cladistics: Definitie, methode en voorbeelden
- EU impasse over onkruidverdelger gaat in beroep
- Wetenschappers vinden nieuwe, lang-hypothetische materiële toestand met handtekening van kwantum-wanordelijke vloeistofachtige magnetische momenten

- Verrassende voorkeur voor eenvoud gevonden in gemeenschappelijk model

- Het oplossen van kale plateaus is de sleutel tot kwantummachine learning

- Akoestische plasmonen gevonden in met gaten gedoteerde cupraatsupergeleiders

- Nieuwe ultrasnelle gele laser klaar voor biomedische toepassingen

 Sneeuwalgen gedijen goed in hooggelegen ijstorens, een onwaarschijnlijke oase voor het leven
Sneeuwalgen gedijen goed in hooggelegen ijstorens, een onwaarschijnlijke oase voor het leven Springer Nature stelt vijf essentiële factoren voor om het delen van gegevens te versnellen
Springer Nature stelt vijf essentiële factoren voor om het delen van gegevens te versnellen Ongelijkheden in het onderwijs hielden aan tijdens tweede periode van schoolsluiting
Ongelijkheden in het onderwijs hielden aan tijdens tweede periode van schoolsluiting Voorgestelde wetenschappelijke normen in New Mexico laten de opwarming van de aarde buiten beschouwing
Voorgestelde wetenschappelijke normen in New Mexico laten de opwarming van de aarde buiten beschouwing 30 miljoen mensen onder hittewaarschuwingen terwijl het westen van de VS broeit
30 miljoen mensen onder hittewaarschuwingen terwijl het westen van de VS broeit Lufthansa vermindert Q1-verliezen terwijl het Air Berlin verteert
Lufthansa vermindert Q1-verliezen terwijl het Air Berlin verteert Studie verklaart sterktekloof tussen grafeen, koolstofvezel
Studie verklaart sterktekloof tussen grafeen, koolstofvezel Chemici kunnen uniforme chiraliteit induceren
Chemici kunnen uniforme chiraliteit induceren
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Portuguese | Swedish | German | Dutch | Danish | Norway | Spanish |

-
Wetenschap © https://nl.scienceaq.com

