
Wetenschap
Systemen van lineaire vergelijkingen oplossen met kwantummechanica
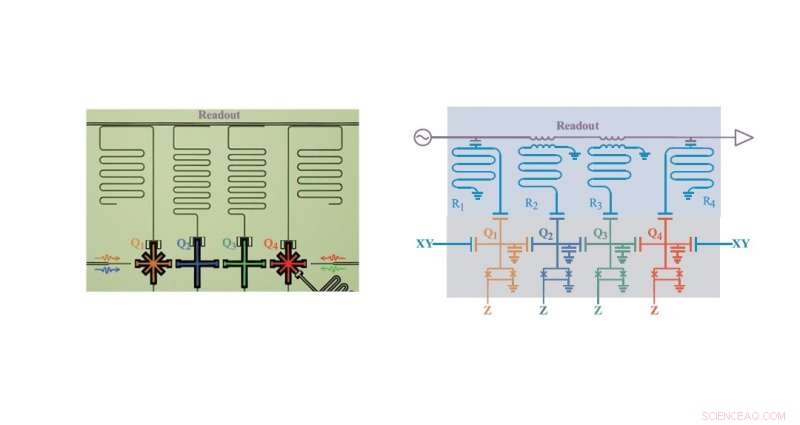
(Links) Foutieve kleurenmicrofoto en (rechts) vereenvoudigd schakelschema van het supergeleidende kwantumcircuit voor het oplossen van 2 × 2 lineaire vergelijkingen. De methode gebruikt vier qubits, gemarkeerd Q1 tot Q4, met vier bijbehorende uitleesresonatoren, gemarkeerd met R1 tot R4. Krediet:Zheng et al. © 2017 American Physical Society
(Phys.org) — Natuurkundigen hebben experimenteel een zuiver kwantummethode gedemonstreerd voor het oplossen van stelsels van lineaire vergelijkingen die het potentieel heeft om exponentieel sneller te werken dan de beste klassieke methoden. De resultaten laten zien dat quantum computing uiteindelijk verregaande praktische toepassingen kan hebben, omdat het oplossen van lineaire systemen vaak wordt gedaan in de wetenschap en techniek.
de fysici, geleid door Haohua Wang aan de Zhejiang University en Chao-Yang Lu en Xiaobo Zhu aan de University of Science and Technology of China, samen met hun co-auteurs van verschillende instellingen in China, hebben hun paper gepubliceerd over wat zij een "quantum lineaire oplosser" noemen in een recent nummer van Fysieke beoordelingsbrieven .
"Voor de eerste keer, we hebben een kwantumalgoritme gedemonstreerd voor het oplossen van stelsels van lineaire vergelijkingen op een supergeleidend kwantumcircuit, " vertelde Lu Phys.org . "[Dit is] een van de beste solid-state platforms met uitstekende schaalbaarheid en opmerkelijke high-fidelity."
Het kwantumalgoritme dat ze hebben geïmplementeerd, heet de Harrow, chassidim, en Lloyd (HHL) algoritme, waarvan eerder werd aangetoond dat het de mogelijkheid heeft, in principe, om te leiden tot een exponentiële kwantumversnelling ten opzichte van klassieke algoritmen. Echter, tot nu toe is dit niet experimenteel aangetoond.
In de nieuwe studie de wetenschappers toonden aan dat een supergeleidend kwantumcircuit met het HHL-algoritme het eenvoudigste type lineair systeem kan oplossen, die twee vergelijkingen met twee variabelen heeft. De methode gebruikt slechts vier qubits:één ancilla qubit (een universeel onderdeel van de meeste kwantumcomputersystemen), en drie qubits die overeenkomen met de invoervector B en de twee oplossingen weergegeven door de oplossingsvector x in het standaard lineaire systeem A x = B , waarbij A een 2 x 2 matrix is.
Door een reeks rotaties uit te voeren, ruilen van staten, en binaire conversies, het HHL-algoritme bepaalt de oplossingen voor dit systeem, die vervolgens kan worden uitgelezen door een quantum non-demolition meting. De onderzoekers demonstreerden de methode met 18 verschillende invoervectoren en dezelfde matrix, het genereren van verschillende oplossingen voor verschillende inputs. Zoals de onderzoekers uitleggen, het is te vroeg om te zeggen hoeveel sneller deze kwantummethode zou kunnen werken, aangezien deze problemen gemakkelijk met klassieke methoden kunnen worden opgelost.
"Het hele rekenproces duurt ongeveer een seconde, "Zei Zhu. "Het is moeilijk om de huidige versie nu direct te vergelijken met de klassieke methoden. In dit werk, we hebben laten zien hoe we het eenvoudigste 2 x 2 lineaire systeem kunnen oplossen, die met klassieke methoden in zeer korte tijd kan worden opgelost. De belangrijkste kracht van het HHL-kwantumalgoritme is dat, bij het oplossen van een 's-sparse' systeemmatrix van een zeer grote omvang, het kan een exponentiële versnelling krijgen in vergelijking met de beste klassieke methode. Daarom, het zou veel interessanter zijn om zo'n vergelijking te laten zien wanneer de grootte van de lineaire vergelijking wordt geschaald naar een zeer groot systeem."
De onderzoekers verwachten dat in de toekomst, dit kwantumcircuit zou kunnen worden opgeschaald om grotere lineaire systemen op te lossen. Ze zijn ook van plan om de prestaties van het systeem verder te verbeteren door enkele eenvoudige aanpassingen aan de fabricage van het apparaat aan te brengen om een deel van de fouten bij de implementatie te verminderen. In aanvulling, de onderzoekers willen onderzoeken hoe het circuit kan worden gebruikt om andere kwantumalgoritmen te implementeren voor verschillende grootschalige toepassingen.
"Ons toekomstig onderzoek zal zich richten op het verbeteren van de hardwareprestaties, inclusief langere coherentietijden, hogere precisie logische poorten, grotere aantallen qubits, lagere overspraak, betere uitlezingsgetrouwheid, enzovoort., " zei Wang. "Op basis van de verbetering van de hardware, we zullen meer kwantumalgoritmen demonstreren en optimaliseren om de kracht van de supergeleidende kwantumprocessor echt te laten zien."
© 2017 Fys.org
 Polymeeronderzoekers ontdekken pad naar duurzame en biologisch afbreekbare polyesters
Polymeeronderzoekers ontdekken pad naar duurzame en biologisch afbreekbare polyesters Wetenschappers gaan diep om de eigenschappen van perovskiet te kwantificeren
Wetenschappers gaan diep om de eigenschappen van perovskiet te kwantificeren Onderzoekers onderzoeken manieren waarop een medicijn als Avandia veiliger kan worden gemaakt
Onderzoekers onderzoeken manieren waarop een medicijn als Avandia veiliger kan worden gemaakt Nieuw biomateriaal kan plastic laminaten vervangen, sterk verminderen vervuiling
Nieuw biomateriaal kan plastic laminaten vervangen, sterk verminderen vervuiling Veiligheidsmaatregelen voor het gebruik van een pipet
Veiligheidsmaatregelen voor het gebruik van een pipet
Hoofdlijnen
- Staan we aan het begin van het einde van de westerse beschaving?
- Wat is de functie van een Tris-buffer in DNA-extractie?
- Hoeveel zintuigen heeft een mens?
- Krachten van spinnengif onderzocht in VR-game
- Nieuw machine learning-systeem kan automatisch vormen van rode bloedcellen identificeren
- Wetenschappers vinden antarctische microben die alleen van lucht leven
- Cellulaire ademhaling in ontkiemende zaden
- Waarom creëren Britse wetenschappers een hybride mens-varken?
- Wat zijn de drie belangrijkste verschillen tussen een plantencel en een dierlijke cel?
- Introductie van een nieuwe isotoop:Mendelevium-244

- Onderzoekers onderzoeken concurrerende staten in supergeleiders bij hoge temperaturen
- Onderzoekers observeren nieuwe, zeer kortlevende neptunium isotoop
- Kwantumonzekerheid helpt een oud probleem op te lossen
- Snapshot-techniek helpt wetenschappers de kwantumwereld te horen

 Een effectieve manier om atrazin en zijn bijproducten in oppervlaktewater te elimineren
Een effectieve manier om atrazin en zijn bijproducten in oppervlaktewater te elimineren Hubble viert zijn 29e verjaardag met ongeëvenaard zicht op de Zuidelijke Krabnevel
Hubble viert zijn 29e verjaardag met ongeëvenaard zicht op de Zuidelijke Krabnevel Leeftijden van het Navajo-zandsteen
Leeftijden van het Navajo-zandsteen Stanine-scores berekenen
Stanine-scores berekenen Grimmige berichten van de wetenschap over klimaatverandering
Grimmige berichten van de wetenschap over klimaatverandering Wie tweet er over wetenschappelijk onderzoek? En waarom?
Wie tweet er over wetenschappelijk onderzoek? En waarom? Hoe polynomen classificeren door Degree
Hoe polynomen classificeren door Degree Wat zijn de eigenschappen van het zichtbare lichtspectrum?
Wat zijn de eigenschappen van het zichtbare lichtspectrum?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

