
Wetenschap
Kwantumfysica biedt nieuwe manier om getallen te factoriseren

Krediet:CC0 Publiek Domein
(Phys.org) - Elk nummer kan, in theorie, te schrijven als het product van priemgetallen. Voor kleine aantallen, dit is eenvoudig (bijvoorbeeld de priemfactoren van 12 zijn 2, 2, en 3), maar voor grote aantallen ontbinden in priemgetallen wordt extreem moeilijk - zo moeilijk dat veel van de hedendaagse cryptografie-algoritmen vertrouwen op de complexiteit van het ontbinden in priemgetallen van getallen met honderden cijfers om privé-informatie veilig te houden.
Echter, niemand weet precies hoe moeilijk het is om zeer grote getallen in hun priemfactoren te ontbinden. Deze vraag, het factorisatieprobleem genoemd, is een van de grootste onopgeloste problemen in de informatica, ondanks het gebruik van geavanceerde wiskundige en computerwetenschappelijke strategieën in pogingen om het op te lossen.
Nu in een nieuwe studie gepubliceerd in Fysieke beoordelingsbrieven , onderzoekers Jose Luis Rosales en Vicente Martin van de Technische Universiteit van Madrid hebben het probleem anders aangepakt.
De onderzoekers hebben aangetoond dat de rekenkunde die wordt gebruikt om getallen in hun priemfactoren te ontbinden, kan worden vertaald in de fysica van een apparaat - een 'kwantumsimulator' - dat de rekenkunde fysiek nabootst in plaats van te proberen een oplossing direct te berekenen zoals een computer doet.
Hoewel de onderzoekers nog geen kwantumsimulator hebben gebouwd, ze laten zien dat de priemfactoren van grote getallen overeenkomen met de energiewaarden van de simulator. Het meten van de energiewaarden zou dan de oplossingen voor een gegeven factoringprobleem opleveren, wat suggereert dat het ontbinden van grote getallen in priemgetallen misschien niet zo moeilijk is als momenteel wordt gedacht.
"Het werk opent een nieuwe weg om getallen te factoriseren, maar we weten nog niets van zijn kracht, " vertelde Rosales Phys.org . "Het is heel opvallend om een volledig nieuwe manier van factoriseren te vinden die rechtstreeks uit de kwantumfysica komt. Het toont niet aan dat het ontbinden van getallen gemakkelijk is, maar het vinden van nieuwe manieren om factoren te bepalen, draagt zeker niet bij aan de kracht van algoritmen op basis van de veronderstelde complexiteit ervan."
Voor nu, de onderzoekers kennen de technische complexiteit van het bouwen van zo'n apparaat niet, of het zelfs mogelijk zou zijn om zeer grote getallen te ontbinden.
"We hebben aangetoond dat er een kwantumsimulator bestaat die getallen kan factoriseren en, in principe, het zou gebouwd kunnen worden, Martin zei. "Of de simulator haalbaar is met de huidige technologie op een manier dat hij getallen van dezelfde grootte kan factoriseren als die welke in cryptografie worden gebruikt, valt nog te bezien, maar de weg is nu open. Het vooruitzicht om zo'n apparaat te bouwen voordat een kwantumcomputer is gebouwd, is iets om serieus over na te denken."
Naar een kwantumgetaltheorie
Naast het potentieel voor praktische toepassingen, de resultaten zijn ook op een meer fundamenteel niveau interessant.
"Naar onze mening, de bijdragen van het papier hebben twee kanten:in pure wiskunde en in toegepaste cryptografie, ' zei Rosales.
Een van de meest wiskundig interessante aspecten van het nieuwe werk is dat het gaat om het herdefiniëren van het factorisatieprobleem door een nieuwe rekenkundige functie te introduceren die vervolgens kan worden toegewezen aan de fysica van de kwantumsimulator en overeenkomt met de energiewaarden. In zekere zin, de onderzoekers herschrijven het wiskundige probleem in termen van natuurkunde.
"Het manuscript probeert de getaltheorie te overbruggen met de kwantumfysica, " zei Rosales, opmerkend dat onderzoekers dit al tientallen jaren proberen te doen. "Tegenwoordig met de ontwikkeling van kwantuminformatie en berekeningen en de ontdekking van Shor's algoritme, de verbinding lijkt intrigerender en belangrijker dan ooit."
Op de lange termijn, dit soort onderzoek zou uiteindelijk kunnen leiden tot een kwantumgetaltheorie - een theorie van getallen die is gebaseerd op fysieke kwantumsystemen.
"Om een kwantumgetaltheorie te ontwikkelen, wat we nodig hebben is een kwantumsysteem (althans een theoretisch) om de priemgetallen te kunnen reproduceren, ' zei Martin. 'In de krant, onze oplossing was om te proberen een systeem te verkrijgen dat een getal in priemgetallen kan ontbinden. De methode is 'analoog' in de zin dat het niet is zoals het algoritme van Shor, die programmeerbaar is in een kwantumcomputer volgens het poortmodel. In plaats daarvan, het is de meting van een zorgvuldig ingesteld kwantumsysteem dat het antwoord geeft.
"Om dit programma uit te voeren, we moeten eerst een rekenkundige formulering van het factorisatieprobleem bedenken die kan worden gekwantiseerd. We moeten een rekenkundige functie vinden, uiteindelijk gerelateerd aan een Hamiltoniaan, en het kwantummechanische probleem zo opzetten dat de oplossing ervan overeenkomt met de oplossing van het factorisatieprobleem. In het werk zijn we erin geslaagd deze ideeën uit te voeren. We hebben de juiste rekenfunctie gevonden, definieerde de factorisatieset om de Hamiltoniaan te binden en verkreeg de oplossing van het kwantummechanische probleem. Voor zover wij weten, dit is nog niet eerder bereikt, hoewel de onze niet de eerste poging was.
"Zoals het altijd wordt gedaan in de natuurkunde, om de resultaten te valideren, we moeten zijn voorspellende capaciteiten bewijzen, dus deden we voorspellingen met hen:verkregen een factorisatie-algoritme dat volledig nieuw is, zonder gelijkenis met enig ander factorisatie-algoritme dat we kennen, en grondig de statistieken van de oplossing vergeleken met de priemgetalstelling.
"De resultaten lieten ons echt versteld staan. Om dit aan te tonen, in het artikel laten we zien hoe het spectrum de prime-telfunctie reproduceert en bijna identiek is aan die van Riemann. Dit wordt verkregen als een direct gevolg van de kwantummechanische theorie en heeft geen tegenhanger in de getaltheorie. Dit tot het uiterste doorvoeren, dit kan zelfs worden beschouwd als de fysica die ten grondslag ligt aan de Riemann-hypothese [een van de belangrijkste open problemen in de getaltheorie] in de zin dat de Hamiltoniaan van nature begrensd is, zonder verdere aannames."
De onderzoekers verklaren dat, In deze krant, ze lieten doorschemeren dat de resultaten diepere wiskundige implicaties hebben, en ze zijn van plan om deze mogelijkheden in de toekomst verder te onderzoeken. Ze onderzoeken ook wat er nodig is om een kwantumsimulator te bouwen.
"We hebben doorlopend onderzoek naar de theorie van het bouwen van een simulator, " zei Rosales. "De eerste indruk is bemoedigend, al is er nog niets beslist."
© 2016 Fys.org
 Verdwijnende Peruaanse gletsjers
Verdwijnende Peruaanse gletsjers We hebben een slimmere oplossing nodig:mensen beschamen voor het vliegen zal de uitstoot van luchtvaartmaatschappijen niet verminderen
We hebben een slimmere oplossing nodig:mensen beschamen voor het vliegen zal de uitstoot van luchtvaartmaatschappijen niet verminderen Tientallen jaren oude verontreinigende stoffen die uit de Himalaya-gletsjers smelten
Tientallen jaren oude verontreinigende stoffen die uit de Himalaya-gletsjers smelten Twee luchtmassa's die een tornado veroorzaken
Twee luchtmassa's die een tornado veroorzaken Zes voet onder, een nieuwe benadering van de opwarming van de aarde
Zes voet onder, een nieuwe benadering van de opwarming van de aarde
Hoofdlijnen
- De effecten van zoutconcentratie op bacteriegroei
- Onderzoekers ontwikkelen CRISPR om enkele RNA-letters in menselijke cellen te bewerken
- Een universele voedsel- en alarmsignaal gevonden in zoogdierbloed
- Heb jij een innerlijke stem? Niet iedereen doet
- Wat is een gen?
- Hadley Cell Effects
- Het is goed om zeldzaam te zijn, voor sommige soorten
- Waarom lijken haaienbeten dodelijker in Australië dan elders?
- Inleiding tot hoe gigantische virussen werken
- Hoe kwantumtechnologie een revolutie teweeg kan brengen in de detectie en behandeling van ziekten

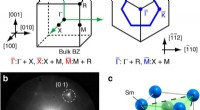
- Het debat beslechten:de elektronische oppervlaktetoestanden van samariumhexaboride oplossen
- Barstende bubbels lanceren bacteriën van water naar lucht
- Concept van nul is eeuwen ouder dan aangenomen,

- Tjilpen is welkom bij vogels, maar niet bij fusie-apparaten - wetenschappers tonen aan dat zwakke turbulentie tsjilpen waarschijnlijker maakt

 Zonne-achtige oscillaties in andere sterren
Zonne-achtige oscillaties in andere sterren Therapeutische antilichamen variëren afhankelijk van het productiesysteem
Therapeutische antilichamen variëren afhankelijk van het productiesysteem Kan Twitter helpen bij rampenbestrijding? Nieuw onderzoek onderzoekt hoe
Kan Twitter helpen bij rampenbestrijding? Nieuw onderzoek onderzoekt hoe Facebook zegt dat er geen teken is dat recente hack zich naar andere apps heeft verspreid
Facebook zegt dat er geen teken is dat recente hack zich naar andere apps heeft verspreid Amerikaans bureau is van plan om de veiligheidsclassificaties voor auto's volgend jaar bij te werken
Amerikaans bureau is van plan om de veiligheidsclassificaties voor auto's volgend jaar bij te werken Nieuwe sensor stuurt elektronisch signaal wanneer oestrogeen wordt gedetecteerd
Nieuwe sensor stuurt elektronisch signaal wanneer oestrogeen wordt gedetecteerd Hoe wordt geometrie in het echte leven gebruikt?
Hoe wordt geometrie in het echte leven gebruikt?  Stijgende zeespiegel creëert eerste inheemse Amerikaanse klimaatvluchtelingen
Stijgende zeespiegel creëert eerste inheemse Amerikaanse klimaatvluchtelingen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

