
Wetenschap
Is het 500.000 of 20.000? Hoe de omvang van een politieke bijeenkomst goed in te schatten

Simulatie van een drukte van twee personen per vierkante meter.
Mijnmagnaat Clive Palmer zorgde vorige week voor controverse toen hij op ABC Radio beweerde dat 500.000 mensen het COVID-"vrijheids"-protest in Melbourne op zaterdag 20 november hadden bijgewoond. Maverick-parlementslid Craig Kelly koos voor de marginaal meer bescheiden "tienduizenden mensen tot nu toe zoals het oog kon zien". De officiële schatting van de politie was 20.000.
De grootte van de menigte is vaak twistpunt geweest. Het Amerikaanse presidentschap van Donald Trump werd geboekt door concurrerende beweringen over de grootte van zijn inauguratiemenigte in januari 2017 en het aantal relschoppers die Capitol Hill bestormden na zijn verkiezingsnederlaag vier jaar later.
Maar waarom zijn de grootte van de menigte zo schijnbaar open voor interpretatie? En wat is de meest nauwkeurige manier om ze te schatten?
Moderne schattingstechnieken voor de grootte van de menigte zijn meestal gebaseerd op de Jacobs-methode, uitgevonden door Herbert Jacobs in de jaren zestig. Jacobs, professor journalistiek aan de University of California, Berkeley, keek naar de demonstranten uit de Vietnamoorlog buiten zijn kantoorraam en merkte dat ze op een geplaveid patroon van zich herhalende vierkanten stonden. Hij telde de studenten in een paar vierkanten, en berekende het gemiddelde aantal studenten per vierkant of menigtedichtheid. Vervolgens vermenigvuldigde hij eenvoudig het aantal vierkanten met de dichtheid om de grootte van de menigte te schatten.
Uit zijn waarnemingen ontdekte hij dat in een lichte menigte elke persoon ongeveer 10 vierkante voet (0,93 vierkante meter) in beslag neemt, terwijl in een dichtere menigte elke persoon minder dan de helft van deze ruimte inneemt. In de meest dicht opeengepakte menigte beslaat elke persoon slechts 2,5 vierkante voet (0,23 vierkante meter) - door onderzoekers aangeduid als "mosh-pit-dichtheid".
Dit wordt beschouwd als een bovengrens voor de massadichtheid, omdat het fysiek niet mogelijk is voor een persoon om minder ruimte in te nemen. Daarom kan elke schatting van de menigte die een dichtheid aanneemt die hoger is dan die van een moshpit veilig worden weggegooid.
Dit basisprincipe wordt door sommige online tools gebruikt om het aantal mensen dat in een bepaald gebied staat in te schatten en te factchecken. In plaats van vierkanten te tellen, wordt het totale gebied vermenigvuldigd met de dichtheid om de schatting van de menigtegrootte te berekenen. De grootte van de menigte in het gemarkeerde gedeelte van de onderstaande Melbourne-kaart wordt bijvoorbeeld geschat op 26.050, gebaseerd op een dichtheid van twee mensen per vierkante meter (we komen zo te weten hoe we de dichtheid van de menigte kunnen schatten).
Hoewel deze tools een behoorlijke ruwe schatting geven van de totale menigte, gaan ze uit van een uniforme verdeling van een menigte over een gebied, wat niet realistisch is. Deze methode houdt ook geen rekening met de ruimte die wordt ingenomen door straatmeubilair, auto's, bomen of andere ruimtes die niet door mensen worden ingenomen.
Mensen kunnen om verschillende redenen bij elkaar komen of zich verspreiden, zoals schaduw zoeken op warme dagen of winderige gebieden in koudere maanden vermijden. Dit kan worden verholpen door met behulp van luchtfoto's verschillende waarschijnlijke dichtheden toe te kennen aan verschillende secties op een kaart. Sommige adviesbureaus beweren dat ze met deze methode het aantal mensen in de tienduizenden tot op 10% kunnen schatten.
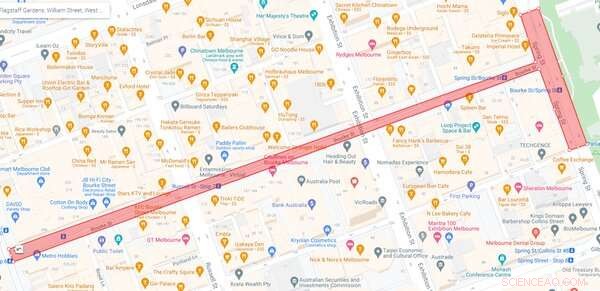
Map showing the approximate area covered by the route from Victoria’s Parliament House to the junction of Bourke St and Swanston St in Melbourne.
Estimating crowd density
Estimating crowd density is crucial to producing a good overall estimate, but this technique is naturally prone to human error. In urban areas, CCTV footage can be used, or digital counting systems such as thermal cameras, although these are expensive if covering a large area. Crowd size can also be indirectly inferred from public transport usage, phone location data, mobile data networks, and social media activity, although this may depend on being able to access companies' proprietary data.
Aerial photography is perhaps the best way to estimate crowd density and size. While ground-based images provide limited views, aerial images offer a literal overview. Images can be collected via satellites, helicopters, balloons or drones (although drones can only be operated by authorized entities in such public spaces). A military satellite image was used to estimate that 800,000 people were present at Barack Obama's presidential inauguration in 2009.
Having collected aerial images or video stills, there are various ways to estimate how many people are within the frame, depending on the image quality and resolution.
AI algorithms can count people by recognizing and counting the distinctive shape of humans, or even just their heads in denser crowds. Statistical methods can also be used to detect the independent motion of the people in the crowd. Or, if the crowd is too packed to count individuals, groups of people can be tracked.
Marchers on the move
It's harder to estimate the size of a mobile crowd than a static one. The crowd density of a political march can vary significantly as people join and leave at various points along the route, and banners or placards can make people effectively invisible to crowd-detection algorithms.
Some researchers suggest using on-ground inspection points where people are counted. The best estimates are likely to involve multiple complementary methods, such as direct counting, aerial and map-based imagery, and public transport data.
Of course, knowing the size of a crowd is about more than just earning bragging rights for politicians. It is a crucial part of crowd management and safety monitoring at large events such as sports fixtures and music concerts.
Aerial monitoring can also spot dangerous crowd congestion or unexpected behavior, and first responders can be provided with an estimate of the number of people who may need help or treatment in the case of an emergency.
 Nieuw elektrodemateriaal ontwikkeld om de laadcapaciteit van lithiumbatterijen te vergroten
Nieuw elektrodemateriaal ontwikkeld om de laadcapaciteit van lithiumbatterijen te vergroten Lab-on-a-chip rijdt op zoek naar nieuwe medicijnen om bloedstolsels te voorkomen
Lab-on-a-chip rijdt op zoek naar nieuwe medicijnen om bloedstolsels te voorkomen Bredere toepassingen voor de unboil an eiermachine
Bredere toepassingen voor de unboil an eiermachine Chemisten HAT-truc voor groenere chemische synthese
Chemisten HAT-truc voor groenere chemische synthese Afzonderlijke moleculen wegen met licht
Afzonderlijke moleculen wegen met licht
 Energiereuzen worden geconfronteerd met een productievermindering van 35% om de klimaatdoelstellingen van Parijs te halen:waakhond
Energiereuzen worden geconfronteerd met een productievermindering van 35% om de klimaatdoelstellingen van Parijs te halen:waakhond Onderzoeker simuleert hoe klimaatverandering de gewasproductie in de landelijke Andes kan beïnvloeden
Onderzoeker simuleert hoe klimaatverandering de gewasproductie in de landelijke Andes kan beïnvloeden Wind verplaatst enorme bosbranden weg van kerncentrales in Idaho
Wind verplaatst enorme bosbranden weg van kerncentrales in Idaho SolarEV City-concept:toekomstige stedelijke energie- en mobiliteitssystemen bouwen
SolarEV City-concept:toekomstige stedelijke energie- en mobiliteitssystemen bouwen Hoe het mondiale klimaat de sedimentaanvoer en de watercondities van het bassin in een jonge kloof beïnvloedt
Hoe het mondiale klimaat de sedimentaanvoer en de watercondities van het bassin in een jonge kloof beïnvloedt
Hoofdlijnen
- Wat is het verschil tussen actieve en passieve transportprocessen?
- COVID-19-medicijnen blijven aanwezig in afvalwater, kunnen een risico vormen voor in het water levende organismen
- Ambtenaren:GGO-muggen zijn geen drugs, EPA-toezicht nodig
- Uitbreiding van Braziliaans suikerriet kan de wereldwijde CO2-uitstoot verminderen
- Science Fair-projecten op handversmettingsmiddelen of vloeibare zeep voor het doden van bacteriën
- De bacteriële gemeenschap op het internationale ruimtestation lijkt op huizen
- Burgerwetenschap kan trends in de vlinderpopulatie voorspellen
- Lijst van forensische technieken
- Aanwijzingen voor de aangeboren resistentie tegen geneesmiddelen van een cacaofermenterende ziekteverwekker
- Voormalig Volkswagen-topman Winterkorn aangeklaagd in VS wegens Dieselgate

- Apple onthult nieuwe iPad van $ 299 voor studenten - ondersteunt AR, Apple Potlood

- Hoe Nederlandse huizen bijna energie- en CO2-neutraal kunnen worden
- Tesla onthult Model Y SUV, uitbreiden naar populair segment

- NASA bestudeert ruimtetoepassingen voor GaN-kristallen

 Duitse energiegigant RWE streeft naar nul koolstof in 2040
Duitse energiegigant RWE streeft naar nul koolstof in 2040 Hoe Foot-Candles naar Lumens
Hoe Foot-Candles naar Lumens Gigantische kwantumtornado's in een hybride licht-materiesysteem geven inzicht in complexe fysieke verschijnselen
Gigantische kwantumtornado's in een hybride licht-materiesysteem geven inzicht in complexe fysieke verschijnselen Nieuwe moleculaire draden voor elektronische apparaten met één molecuul
Nieuwe moleculaire draden voor elektronische apparaten met één molecuul Amazon-vooruitzichten - aanhoudende opwarming, meerjarige droogte
Amazon-vooruitzichten - aanhoudende opwarming, meerjarige droogte Geoptimaliseerde hoortoestellen met glasvezeltechnologie
Geoptimaliseerde hoortoestellen met glasvezeltechnologie Voedselbezorgers in Frankrijk beloven afval te verminderen
Voedselbezorgers in Frankrijk beloven afval te verminderen Onderzoek onthult nieuwe staat van materie:een Cooper-paar metaal
Onderzoek onthult nieuwe staat van materie:een Cooper-paar metaal
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

