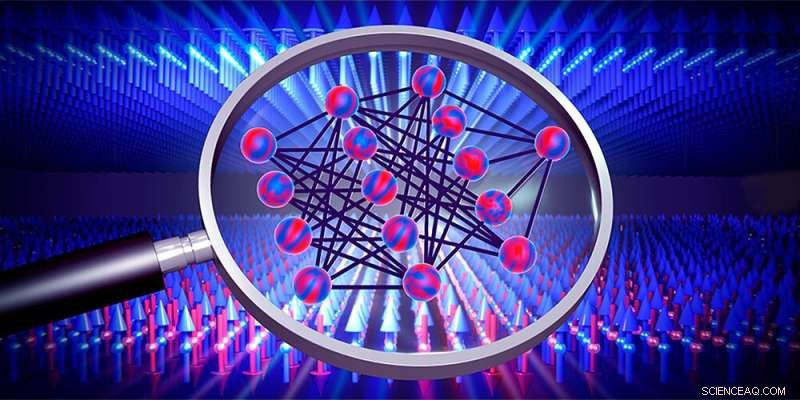
Neurale netwerken zijn leeralgoritmen die de oplossing voor een taak benaderen door te trainen met beschikbare gegevens. Het is echter meestal onduidelijk hoe ze dit precies bereiken. Twee jonge Bazelse natuurkundigen hebben nu wiskundige uitdrukkingen afgeleid waarmee je de optimale oplossing kunt berekenen zonder een netwerk te hoeven trainen. Hun resultaten geven niet alleen inzicht in hoe die leeralgoritmen werken, maar kunnen in de toekomst ook helpen om onbekende faseovergangen in fysieke systemen te detecteren.

Neurale netwerken zijn gebaseerd op het werkingsprincipe van de hersenen. Dergelijke computeralgoritmen leren door herhaalde training problemen op te lossen en kunnen bijvoorbeeld objecten onderscheiden of gesproken taal verwerken.

Sinds enkele jaren proberen natuurkundigen ook neurale netwerken te gebruiken om faseovergangen te detecteren. Faseovergangen zijn ons bekend uit de dagelijkse ervaring, bijvoorbeeld wanneer water bevriest tot ijs, maar ze komen ook in meer complexe vorm voor tussen verschillende fasen van magnetische materialen of kwantumsystemen, waar ze vaak moeilijk te detecteren zijn.

Julian Arnold en Frank Schäfer, twee Ph.D. studenten in de onderzoeksgroep van Prof. Dr. Christoph Bruder aan de Universiteit van Basel, hebben nu eigenhandig wiskundige uitdrukkingen afgeleid waarmee dergelijke faseovergangen sneller dan voorheen ontdekt kunnen worden. Ze publiceerden onlangs hun resultaten in Physical Review X .

Training overslaan bespaart tijd

Een neuraal netwerk leert door in veel trainingsrondes systematisch parameters te variëren om de door het netwerk berekende voorspellingen steeds beter af te stemmen op de ingevoerde trainingsgegevens. Die trainingsgegevens kunnen de pixels van afbeeldingen zijn of in feite de resultaten van metingen op een fysiek systeem met faseovergangen waarover men iets zou willen leren.

"Neurale netwerken zijn al behoorlijk goed geworden in het detecteren van faseovergangen", zegt Arnold, "maar hoe ze dat precies doen, blijft meestal volledig onduidelijk." Om die situatie te veranderen en wat licht in de "black box" van een neuraal netwerk te laten schijnen, keken Arnold en Schäfer naar het speciale geval van netwerken met een oneindig aantal parameters die in principe ook oneindig veel trainingsrondes doorlopen.

Over het algemeen is het al lang bekend dat de voorspellingen van dergelijke netwerken altijd neigen naar een bepaalde optimale oplossing. Arnold en Schäfer namen dit als uitgangspunt voor het afleiden van wiskundige formules waarmee je die optimale oplossing direct kunt berekenen zonder dat je het netwerk daadwerkelijk hoeft te trainen. "Die snelkoppeling vermindert de rekentijd enorm", legt Arnold uit:"De tijd die nodig is om onze oplossing te berekenen, is slechts zo lang als een enkele trainingsronde van een klein netwerk."

Inzicht in het netwerk

Naast tijdwinst heeft de door de Bazelse fysici ontwikkelde methode ook het voordeel dat de afgeleide vergelijkingen enig inzicht geven in de werking van de neurale netwerken en daarmee van de onderzochte fysische systemen.

Tot nu toe hebben Arnold en Schäfer hun methode getest op door de computer gegenereerde gegevens. Binnenkort willen ze de methode ook toepassen op echte meetgegevens. Hiermee kunnen in de toekomst nog onbekende faseovergangen worden gedetecteerd, bijvoorbeeld in kwantumsimulatoren of in nieuwe materialen. + Verder verkennen

Nieuwe methode om neurale netwerken te vergelijken legt bloot hoe kunstmatige intelligentie werkt