
Wetenschap
Wat is het percentage ionisatie van ammoniak bij deze concentratie?
$$Kb =\frac{[NH4+][OH-]}{[NH3]}$$
waarbij Kb de base-ionisatieconstante is voor ammoniak, [NH4+] de concentratie ammoniumionen is, [OH-] de concentratie hydroxide-ionen is en [NH3] de concentratie ammoniak is.
Bij een concentratie van 0,1 M is de ionisatie van ammoniak niet significant en kan de concentratie van ammoniumionen en hydroxide-ionen als verwaarloosbaar worden beschouwd vergeleken met de concentratie van ammoniak. Daarom kunnen we de evenwichtsconstante-uitdrukking vereenvoudigen tot:
$$Kb =\frac{[OH-]^2}{[NH3]}$$
Uitgaande van volledige dissociatie van water, is de concentratie van hydroxide-ionen gelijk aan de vierkantswortel van het ionische product van water (Kw):
$$[OH-] =\sqrt{Kw} =\sqrt{1,0 \maal 10^{-14}} =1,0 \maal 10^{-7} \ M$$
Als we de concentratie van hydroxide-ionen vervangen door de vereenvoudigde evenwichtsconstante-uitdrukking, krijgen we:
$$Kb =\frac{(1,0 \times 10^{-7})^2}{[NH3]}$$
$$[NH3] =\frac{1,0 \tijden 10^{-14}}{Kb} =\frac{1,0 \tijden 10^{-14}}{1,8 \tijden 10^{-5}} =5,56 \ maal 10^{-10} \ M$$
Het percentage ionisatie van ammoniak wordt als volgt berekend:
$$Percentage \ ionisatie =\frac{[NH4+]}{[NH3] + [NH4+]} \times 100$$
Omdat de concentratie ammoniumionen verwaarloosbaar is in vergelijking met de concentratie ammoniak, kunnen we de uitdrukking vereenvoudigen tot:
$$Percentage \ ionisatie =\frac{[NH4+]}{[NH3]} \times 100$$
Als we de ammoniakconcentratie vervangen die we eerder hebben berekend, krijgen we:
$$Percentage \ ionisatie =\frac{5,56 \times 10^{-10}}{0,1} \times 100 =5,56 \times 10^{-9} \%$$
Daarom is het percentage ionisatie van ammoniak bij een concentratie van 0,1 M ongeveer 5,56 × 10^{-9}%.
 Versnelde analyse van de stabiliteit van complexe legeringen
Versnelde analyse van de stabiliteit van complexe legeringen Wanneer de vergelijking Fe3O4 plus Al - Al2O3 Fe correct in evenwicht is, welke coëfficiënt van Fe?
Wanneer de vergelijking Fe3O4 plus Al - Al2O3 Fe correct in evenwicht is, welke coëfficiënt van Fe?  Bacteriën opsnuiven:team ontwikkelt een nieuwe aanpak voor snelle identificatie van bacteriesoorten
Bacteriën opsnuiven:team ontwikkelt een nieuwe aanpak voor snelle identificatie van bacteriesoorten  Vergrendelde MOF's zijn de sleutel tot hoge porositeit
Vergrendelde MOF's zijn de sleutel tot hoge porositeit Wat zijn eiwitten die bepaalde chemische reacties versnellen?
Wat zijn eiwitten die bepaalde chemische reacties versnellen?
Hoofdlijnen
- Waarom produceert kernsplijting peervormige kernen?
- Hoe dicht is een cel? Onderzoekers hebben een manier bedacht om die vraag te beantwoorden
- Wetenschappers ontdekken hoe hormonen hun effecten bereiken
- Hoe het menselijk geheugen werkt
- Wetenschappers koppelen eicelspecifieke histon H1FOO aan een betere iPS-celgeneratie
- Hoe breuken in DNA worden gerepareerd
- Duwen, trekken of draaien:de vele bewegingen van trilhaartjes
- De prehistorische meersteur is niet bedreigd, zeggen de VS, ondanks oproepen van natuurbeschermers
- Help, bijen hebben de muren van mijn huis gekoloniseerd! Waarom zijn ze daar en wat moet ik doen?
- Nieuwe methode keert de zelfassemblage van vloeibare kristallen om

- Onderzoekers maken superlijm op basis van slangengif die het bloeden binnen enkele seconden stopt met zichtbaar licht

- Biochemici ontdekken hoe reactieve zuurstofsoorten de cisplatineresistentie in eierstokkankercellen beïnvloeden

- Onderzoekers ontdekken ongebruikelijk celdodend mechanisme voor moleculen

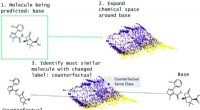
- Contrafeiten gebruiken om voorspellingen over de veiligheid van geneesmiddelen te verifiëren
 Al slecht af, alleenstaande ouders gingen dramatisch achteruit tijdens COVID
Al slecht af, alleenstaande ouders gingen dramatisch achteruit tijdens COVID Waar gebruikt het lichaam ATP voor?
Waar gebruikt het lichaam ATP voor?  Pesten, intimidatie en uitbuiting zijn allemaal in een dag werk in de horeca
Pesten, intimidatie en uitbuiting zijn allemaal in een dag werk in de horeca  Regen biedt hoop op Australische bosbranden maar rook raakt tennissterren
Regen biedt hoop op Australische bosbranden maar rook raakt tennissterren Hoe raketten werken
Hoe raketten werken  Grote ongelijkheid in rijkdom gekoppeld aan meer steun voor populistische leiders
Grote ongelijkheid in rijkdom gekoppeld aan meer steun voor populistische leiders Toekomst helder voor mini-synchrotrons
Toekomst helder voor mini-synchrotrons De fenomenologie van onveiligheid en veiligheid
De fenomenologie van onveiligheid en veiligheid
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

