Wetenschap
Donkere materie:onze recensie suggereert dat het tijd is om het te dumpen ten gunste van een nieuwe zwaartekrachttheorie

Het balkspiraalstelsel UGC 12158. Credit:Wikimedia, CC BY-SA
We kunnen de bewegingen van planeten in het zonnestelsel vrij nauwkeurig modelleren met behulp van de natuurwetten van Newton. Maar in het begin van de jaren zeventig merkten wetenschappers dat dit niet werkte voor schijfsterrenstelsels - sterren aan hun buitenranden, ver van de zwaartekracht van alle materie in hun centrum - bewogen veel sneller dan de theorie van Newton voorspelde.
Dit deed natuurkundigen vermoeden dat een onzichtbare substantie genaamd 'donkere materie' voor extra zwaartekracht zorgde, waardoor de sterren versnelden - een theorie die enorm populair is geworden. In een recent overzicht hebben mijn collega's en ik echter gesuggereerd dat waarnemingen over een groot aantal schalen veel beter kunnen worden verklaard in een alternatieve zwaartekrachttheorie, voorgesteld door de Israëlische natuurkundige Mordehai Milgrom in 1982, genaamd Milgromian dynamics of Mond, waarvoor geen onzichtbare materie nodig is.
Monds belangrijkste postulaat is dat wanneer de zwaartekracht erg zwak wordt, zoals aan de rand van sterrenstelsels, deze zich anders gaat gedragen dan de Newtoniaanse fysica. Op deze manier is het mogelijk te verklaren waarom sterren, planeten en gas in de buitenwijken van meer dan 150 sterrenstelsels sneller roteren dan verwacht op basis van alleen hun zichtbare massa. Maar Mond legt niet alleen uit dergelijke rotatiecurven, in veel gevallen, voorspelt hen.
Wetenschapsfilosofen hebben betoogd dat deze voorspellingskracht Mond superieur maakt aan het standaard kosmologische model, dat stelt dat er meer donkere materie in het universum is dan zichtbare materie. Dit komt omdat, volgens dit model, sterrenstelsels een zeer onzekere hoeveelheid donkere materie hebben die afhangt van details over hoe het sterrenstelsel is gevormd - wat we niet altijd weten. Dit maakt het onmogelijk om te voorspellen hoe snel sterrenstelsels zouden moeten roteren. Maar dergelijke voorspellingen worden routinematig gedaan met Mond, en tot nu toe zijn deze bevestigd.
Stel je voor dat we de verdeling van zichtbare massa in een melkwegstelsel kennen, maar de rotatiesnelheid ervan nog niet. In het standaard kosmologische model zou alleen met enige zekerheid kunnen worden gezegd dat de rotatiesnelheid aan de rand zal uitkomen tussen 100 km/s en 300 km/s. Mond maakt een meer definitieve voorspelling dat de rotatiesnelheid in het bereik van 180-190 km/s moet liggen.
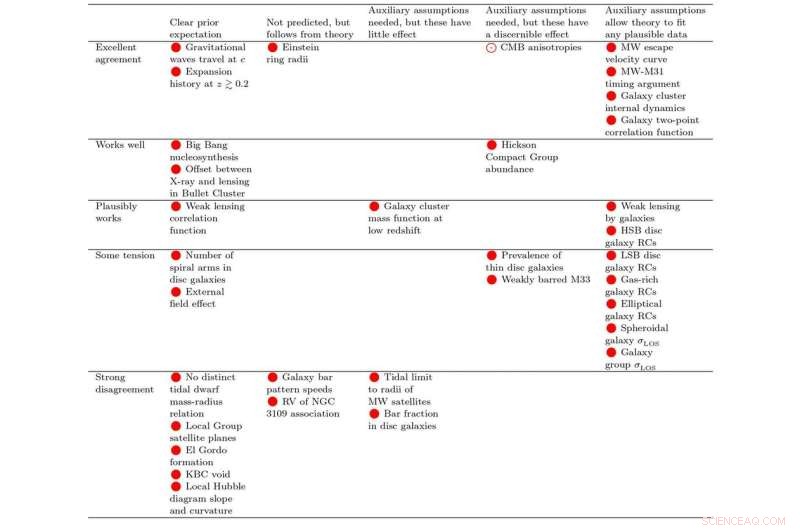
Vergelijking van het standaard kosmologische model met waarnemingen op basis van hoe goed de gegevens overeenkomen met de theorie (verbetering van beneden naar boven) en hoeveel flexibiliteit het had in de pasvorm (van links naar rechts stijgend). De holle cirkel wordt niet meegeteld in onze beoordeling, omdat die gegevens zijn gebruikt om parameters vrij te geven. Overgenomen uit tabel 3 van onze recensie. Krediet:Arxiv
Als observaties later een rotatiesnelheid van 188 km/s laten zien, dan is dit in overeenstemming met beide theorieën, maar het is duidelijk dat Mond de voorkeur heeft. Dit is een moderne versie van het scheermes van Occam - dat de eenvoudigste oplossing de voorkeur verdient boven de meer complexe, in dit geval dat we waarnemingen moeten verklaren met zo min mogelijk "vrije parameters". Vrije parameters zijn constanten - bepaalde getallen die we in vergelijkingen moeten pluggen om ze te laten werken. Maar ze worden niet door de theorie zelf gegeven - er is geen reden waarom ze een bepaalde waarde zouden moeten hebben - dus we moeten ze observationeel meten. Een voorbeeld is de gravitatieconstante, G, in de zwaartekrachttheorie van Newton of de hoeveelheid donkere materie in sterrenstelsels binnen het standaard kosmologische model.
We hebben een concept geïntroduceerd dat bekend staat als 'theoretische flexibiliteit' om het onderliggende idee van het scheermes van Occam vast te leggen dat een theorie met meer vrije parameters consistent is met een breder scala aan gegevens, waardoor het complexer wordt. In onze review hebben we dit concept gebruikt bij het testen van het standaard kosmologische model en Mond tegen verschillende astronomische waarnemingen, zoals de rotatie van sterrenstelsels en de bewegingen binnen clusters van sterrenstelsels.
Elke keer gaven we een theoretische flexibiliteitsscore tussen –2 en +2. Een score van -2 geeft aan dat een model een duidelijke, nauwkeurige voorspelling doet zonder naar de gegevens te kijken. Omgekeerd betekent +2 "alles mag" - theoretici zouden in staat zijn geweest om bijna elk aannemelijk waarnemingsresultaat te passen (omdat er zoveel vrije parameters zijn). We hebben ook beoordeeld hoe goed elk model overeenkomt met de waarnemingen, waarbij +2 een uitstekende overeenkomst aangeeft en -2 gereserveerd voor waarnemingen die duidelijk aantonen dat de theorie verkeerd is. Vervolgens trekken we de theoretische flexibiliteitsscore af van die voor de overeenstemming met waarnemingen, aangezien het goed is om de gegevens goed te matchen, maar alles kunnen passen is slecht.
Een goede theorie zou duidelijke voorspellingen doen die later worden bevestigd, en idealiter een gecombineerde score van +4 krijgen in veel verschillende tests (+2 -(-2) =+4). Een slechte theorie zou een score krijgen tussen 0 en -4 (-2 -(+2)=-4). Nauwkeurige voorspellingen zouden in dit geval mislukken - het is onwaarschijnlijk dat deze werken met de verkeerde fysica.
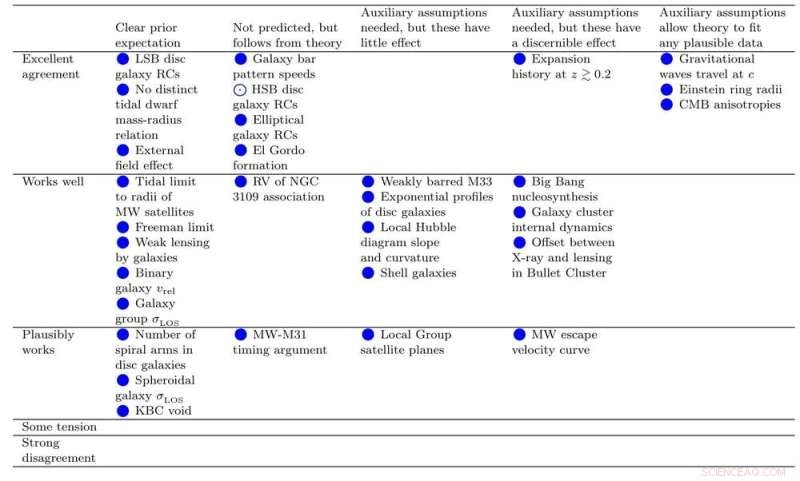
We vonden een gemiddelde score voor het standaard kosmologische model van -0,25 over 32 tests, terwijl Mond een gemiddelde van +1,69 behaalde over 29 tests. De scores voor elke theorie in veel verschillende tests worden weergegeven in figuur 1 en 2 hieronder voor respectievelijk het standaard kosmologische model en Mond.
Het is meteen duidelijk dat er geen grote problemen zijn geïdentificeerd voor Mond, wat op zijn minst aannemelijk is met alle gegevens (merk op dat de onderste twee rijen die vervalsingen aanduiden leeg zijn in de onderstaande figuur).
Het balkspiraalstelsel UGC 12158. Credit:Wikimedia, CC BY-SA
De problemen met donkere materie
Een van de meest opvallende tekortkomingen van het standaard kosmologische model heeft betrekking op "sterrenstelsels" - staafvormige heldere gebieden gemaakt van sterren - die spiraalstelsels vaak in hun centrale gebieden hebben (zie afbeelding lood). De staven roteren in de tijd. Als sterrenstelsels zouden zijn ingebed in massieve halo's van donkere materie, zouden hun staven langzamer worden. De meeste, zo niet alle, waargenomen sterrenstelsels zijn echter snel. Dit vervalst het standaard kosmologische model met zeer veel vertrouwen.
Een ander probleem is dat de originele modellen die sterrenstelsels suggereerden halo's van donkere materie hebben, een grote fout hebben gemaakt - ze gingen ervan uit dat de donkere materiedeeltjes zwaartekracht gaven aan de materie eromheen, maar niet werden beïnvloed door de zwaartekracht van de normale materie. Dit vereenvoudigde de berekeningen, maar het weerspiegelt niet de werkelijkheid. Toen hiermee in latere simulaties rekening werd gehouden, was het duidelijk dat halo's van donkere materie rond sterrenstelsels hun eigenschappen niet betrouwbaar verklaren.
Er zijn veel andere tekortkomingen van het standaard kosmologische model dat we in onze review hebben onderzocht, waarbij Mond vaak in staat is om de waarnemingen op natuurlijke wijze te verklaren. De reden dat het standaard kosmologische model desondanks zo populair is, kan te maken hebben met rekenfouten of beperkte kennis over de fouten ervan, waarvan sommige vrij recent zijn ontdekt. Het kan ook te wijten zijn aan de onwil van mensen om een zwaartekrachttheorie aan te passen die zo succesvol is geweest op veel andere gebieden van de natuurkunde.
De enorme voorsprong van Mond op het standaard kosmologische model in onze studie bracht ons tot de conclusie dat Mond sterk de voorkeur geniet van de beschikbare waarnemingen. Hoewel we niet beweren dat Mond perfect is, denken we nog steeds dat het het grote plaatje correct geeft - sterrenstelsels hebben echt geen donkere materie. + Verder verkennen
Nieuwe draai aan melkwegrotatie redt controversiële zwaartekrachttheorie
Dit artikel is opnieuw gepubliceerd vanuit The Conversation onder een Creative Commons-licentie. Lees het originele artikel. 
 Wat is ondoorzichtig plastic?
Wat is ondoorzichtig plastic?  Nieuw model voor bimoleculaire reacties in nanoreactoren
Nieuw model voor bimoleculaire reacties in nanoreactoren De onzichtbare katalysator die chemische reacties kan stimuleren
De onzichtbare katalysator die chemische reacties kan stimuleren Chemici ontdekken het mechanisme van stralingsinstabiliteit van lithiumtetraboraat
Chemici ontdekken het mechanisme van stralingsinstabiliteit van lithiumtetraboraat Watermoleculen uit elkaar halen om schone brandstof te genereren:onderzoek naar een veelbelovend materiaal
Watermoleculen uit elkaar halen om schone brandstof te genereren:onderzoek naar een veelbelovend materiaal
 Onderzoekers schatten buitengewone koolstofemissies van door El Nino geïnduceerde verbranding van biomassa
Onderzoekers schatten buitengewone koolstofemissies van door El Nino geïnduceerde verbranding van biomassa NASA ziet tropische cycloon Irondro een oog ontwikkelen
NASA ziet tropische cycloon Irondro een oog ontwikkelen Effecten van ozonafbraak gevoeld in de tropen
Effecten van ozonafbraak gevoeld in de tropen Wat zijn de kenmerken van overstromingen?
Wat zijn de kenmerken van overstromingen?  Gemodificeerde klei kan herbicide uit water verwijderen
Gemodificeerde klei kan herbicide uit water verwijderen
Hoofdlijnen
- Chili vecht om een favoriete mossel te redden
- Vijf soorten aseksuele reproductie
- Is genie genetisch?
- Dolfijnen gebruiken kenmerkende fluitjes om andere dolfijnen te vertegenwoordigen, vergelijkbaar met hoe mensen namen gebruiken
- 3 fasen van interfase
- Landbouwfungicide trekt honingbijen aan, studie vondsten
- Pelagische zeevogels vliegen in het oog van de storm wanneer ze worden geconfronteerd met extreme weersomstandigheden
- De zoektocht naar de zuidelijke rubberboa
- rRNA: Wat is het?
 Waarom kokende druppels over hete olieachtige oppervlakken kunnen racen
Waarom kokende druppels over hete olieachtige oppervlakken kunnen racen Menselijke schedel uit het Midden-Pleistoceen onthult variatie en continuïteit bij vroege Aziatische mensen
Menselijke schedel uit het Midden-Pleistoceen onthult variatie en continuïteit bij vroege Aziatische mensen De eerste stap naar het kiezen van de juiste universiteit? Negeer de ranglijst
De eerste stap naar het kiezen van de juiste universiteit? Negeer de ranglijst Nu in 3D:Deep learning-technieken helpen bij het visualiseren van röntgengegevens in drie dimensies
Nu in 3D:Deep learning-technieken helpen bij het visualiseren van röntgengegevens in drie dimensies Gaat het waaien? Vulkanische emissies vanuit de ruimte meten
Gaat het waaien? Vulkanische emissies vanuit de ruimte meten Transformatie door licht
Transformatie door licht Wil je de wereldproblemen oplossen? Probeer samen te werken over disciplines heen
Wil je de wereldproblemen oplossen? Probeer samen te werken over disciplines heen Studie van oude vissen suggereert dat Chicxulub-asteroïde de verwarmde planeet voor 100, 000 jaar
Studie van oude vissen suggereert dat Chicxulub-asteroïde de verwarmde planeet voor 100, 000 jaar
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com