
Wetenschap
Tweedimensionale materialen krijgen een nieuwe theorie voor het beheersen van eigenschappen
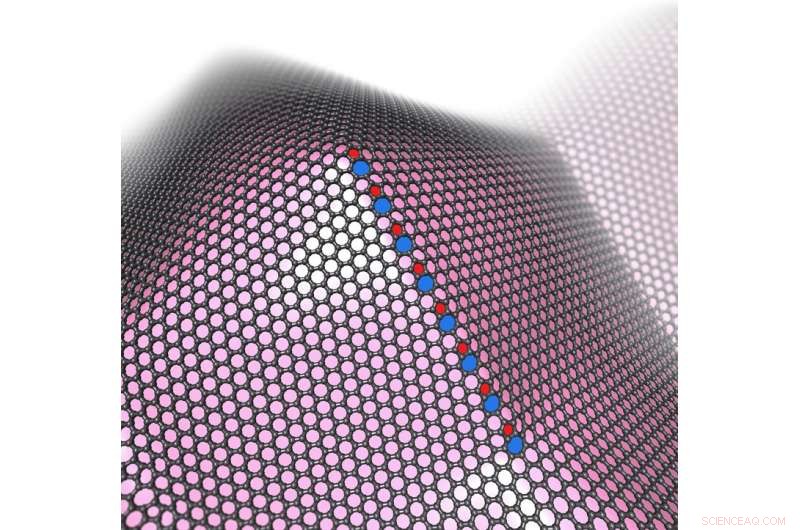
Een korrelgrens vormt zich wanneer grafeengroei voorbij een top op een conische bult gaat, waarbij de kromming lijkt op die op een bol; het eindigt aan de voet van de bult, waar de kromming zadelachtig is. Krediet:Crespi, Penn State
Gewenste eigenschappen waaronder verhoogde elektrische geleidbaarheid, verbeterde mechanische eigenschappen, of magnetisme voor geheugenopslag of informatieverwerking kan mogelijk zijn vanwege een theoretische methode om korrelgrenzen in tweedimensionale materialen te controleren, volgens materiaalwetenschappers van Penn State.
Tweedimensionale (2D) materialen zijn de afgelopen tien jaar het onderwerp geweest van intensief onderzoek, maar voorafgaand aan het werk van Yuanxi Wang, een recent doctoraat in Penn State en Vincent H. Crespi, vooraanstaand hoogleraar natuurkunde, materiaalwetenschap en techniek en scheikunde bij Penn State, niemand had een algemene manier bedacht om de locatie en het type korrelgrenzen in 2D-materialen te controleren.
"Als je een 2D-materiaal kweekt, een dunne film, je deponeert materialen op een ondergrond, " legde Crespi uit. "Als de atomen op het substraat vallen, ze organiseren zichzelf in kristallijne gebieden die korrels worden genoemd."
Als de korrels uitzetten, ze komen in andere groeiende kristallijne gebieden terecht, en waar ze elkaar ontmoeten, wordt de korrelgrens genoemd. Maar zoals een vloer betegelen door de tegels willekeurig te gooien, de oriëntatie van de korrels en korrelgrenzen zijn willekeurig, wat de materiaaleigenschappen beïnvloedt.
Tot dit werk, gepubliceerd in het tijdschrift Nano-letters , deze willekeurige korrelgrenzen werden grotendeels beschouwd als ongelukkige bijproducten van het afzettingsproces.
"Typisch, wanneer je een materiaal kweekt, die willekeurige korrelgrenzen zijn slecht, "zei Crespi. "De atomen paren niet met elkaar zoals in gewone kristallen. Stroom en warmte gaan niet gemakkelijk door. Ze hebben de neiging om warmte en elektronen te verspreiden."
Crespi en Wang hadden het idee dat door het onderliggende substraat te manipuleren, ze konden vooraf bepalen waar de korrelgrenzen zouden beginnen en eindigen, en laat ze op een geordende positie staan. De belangrijkste vormen waren gebaseerd op iets dat Gauss-kromming wordt genoemd, een reeks halfronde hobbels en kuilen op een substraat dat lijkt op een eierdoos.
Wang deed berekeningen die aantoonden dat voor twee veel bestudeerde 2D-materialen, grafeen en molybdeendisulfide, de groei zou op specifieke locaties korrelgrenzen vormen in plaats van los te komen van het substraat of ongewenste plooien te ontwikkelen. Als het 2D-materiaal niet goed hecht aan de ondergrond, het zal een vouw genereren.
"We ontdekten dat de energie en kinetiek van het vormen van korrelgrenzen versus een vouw of onthechting, waren gunstig in grafeen en molybdeendisulfide, en toepasbaar op elk 2D-materiaal, " zei Wang. "Maar geen enkele hobbel zou voldoende zijn. Ze moeten een Gaussiaanse kromming hebben."
Toepassingen zijn onder meer geheugenopslag, waarbij het regelen van de magnetische toestand van een 2D magnetisch-korrelgrenssysteem door het aanleggen van een spanning een zeer nuttige mogelijkheid zou zijn. De fijne controle van elektronische eigenschappen via korrelgrenzen kan ook worden gebruikt in spintronica, die informatie verwerkt met behulp van de spin van elektronen. Deze korrelgrenzen bepalen vaak ook de mechanische eigenschappen van materialen, zoals hoe ze reageren onder uitrekken.
"Dit geeft mensen een nieuwe manier van denken over het optimaliseren van de eigenschappen van 2D-materialen waar ze meer controle hebben dan voorheen, "Zei Crespi. "We wisten niet dat we zo'n fijne controle over de korrelgrenzen konden hebben, en dus dachten we er niet aan om de magnetische, thermische en elektronische eigenschappen van korrelgrenzen met het oog op het creëren van 'korrelgrensmaterialen' waarvan de eigenschappen worden bepaald door een gecontroleerde verdeling van gespecificeerde korrelgrenzen."
Hun artikel in Nano-letters is getiteld "Theory of Finite-Length Grain Boundaries of Controlled Misfit Angle in Two-Dimensional Materials."
 Een materiaalgeheugen gebruiken om unieke fysieke eigenschappen te coderen
Een materiaalgeheugen gebruiken om unieke fysieke eigenschappen te coderen Onder druk:eiwit-nabootsende moleculen manipuleren met hydrostatische druk
Onder druk:eiwit-nabootsende moleculen manipuleren met hydrostatische druk Zuurtegraad van functionele groepen
Zuurtegraad van functionele groepen  Onderzoekers creëren sterke, snel, waterdichte lijm
Onderzoekers creëren sterke, snel, waterdichte lijm Kan kunstmatige intelligentie nieuwe deuren openen voor het ontdekken van materialen?
Kan kunstmatige intelligentie nieuwe deuren openen voor het ontdekken van materialen?
 Wat zijn de zeekoeienaanpassingen voor overleving?
Wat zijn de zeekoeienaanpassingen voor overleving?  Canadezen pakken koelcentra in terwijl dodental hittegolf verdubbelt
Canadezen pakken koelcentra in terwijl dodental hittegolf verdubbelt Hawaiian Airlines sluit zich aan bij internationaal onderzoek naar klimaatverandering
Hawaiian Airlines sluit zich aan bij internationaal onderzoek naar klimaatverandering Verlies van veerkracht gebruiken als een vroeg waarschuwingssignaal om de kans op bossterfte te voorspellen
Verlies van veerkracht gebruiken als een vroeg waarschuwingssignaal om de kans op bossterfte te voorspellen Laat het sneeuwen:onderzoekers testen cloud seeding
Laat het sneeuwen:onderzoekers testen cloud seeding
Hoofdlijnen
- Slimme app gebruikt smartphonecamera om plantensoorten te identificeren
- Interferentie berekenen
- Soorten forensische tests
- Vissen en schepen:het scheepvaartverkeer verkleint het communicatiebereik voor Atlantische kabeljauw, Schelvis
- Dierlijke versus plantencellen: overeenkomsten en verschillen (met grafiek)
- Planten kunnen kiezen tussen alternatieve reacties op concurrentie
- Model voorspelt hoe E. coli-bacteriën zich aanpassen onder stress
- Wat is troebelheid en wat staat er in de microbiologie?
- Vervangt je lichaam zichzelf echt elke zeven jaar?
- Onderzoekers bewijzen dat composieten van titanaat nanobuisjes de fotokatalyse van waterstof verbeteren
- Nieuwe tool helpt nanostaafjes op te vallen
- Met nanobuisjes, genetische manipulatie in planten is easy-peasy

- Nano-ingenieurs kunnen in enkele seconden 3D-microstructuren printen
- Onderzoekers ontwikkelen harder keramiek voor pantserramen

 Toekomstige gevolgen van El Niño, La Niña zal waarschijnlijk intensiveren, toenemende bosbranden, droogterisico
Toekomstige gevolgen van El Niño, La Niña zal waarschijnlijk intensiveren, toenemende bosbranden, droogterisico DNA-origami overtreft belangrijke drempels
DNA-origami overtreft belangrijke drempels Bergen op de maan vergelijken met de toppen van de aarde
Bergen op de maan vergelijken met de toppen van de aarde Amazon zegt dat drone-leveringen binnen enkele maanden komen
Amazon zegt dat drone-leveringen binnen enkele maanden komen Burn-out van leraren veroorzaakt uittocht uit het beroep, studie vondsten
Burn-out van leraren veroorzaakt uittocht uit het beroep, studie vondsten Duitsland geeft keurmerk aan vrachtwagendraaiassistent
Duitsland geeft keurmerk aan vrachtwagendraaiassistent Vijandige leraren kunnen studenten 5 procent verliezen op testscores
Vijandige leraren kunnen studenten 5 procent verliezen op testscores Gebruik van magneten in ons dagelijks leven
Gebruik van magneten in ons dagelijks leven
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

