
Wetenschap
Bewijs voor vaste-vloeistof-kritische punten van water in koolstofnanobuisjes
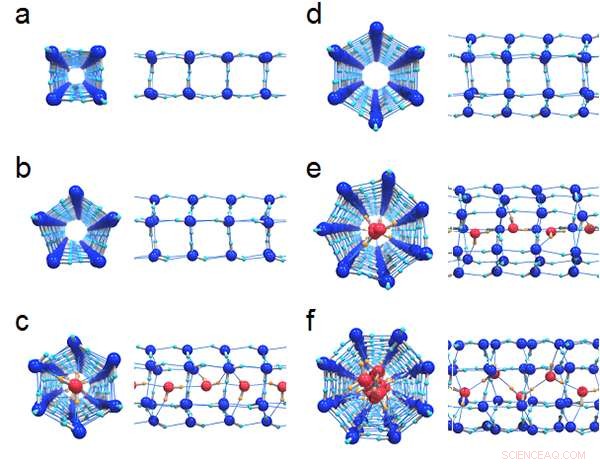
Figuur 1:Waterstofbindingsstructuren van zes ijsjes gevormd in de nanobuisjes:(a) (4, 0)ijs, (b) (5, 0) ijs en (c) gevuld (6, 0) ijs met een diameter van 1,11 nm, (d) (6, 0) ijs, (e) gevuld (7, 0) ijs en (f) gevuld (8, 0) ijs met een diameter van 1,25 nm. Bovenaanzichten en het bijbehorende zijaanzicht zijn naast elkaar getekend. Centrale watermoleculen die een ketting vormen in het gevulde ijs, zijn rood gekleurd om ze te onderscheiden van de buitenste ringen.
Veel natuurkundigen accepteren het idee niet dat een vast-vloeibaar fasegrens kan eindigen op een kritiek punt - een unieke toestand waarin twee fasen hun afzonderlijke identiteit verliezen. Waarom doen ze dat niet? Het gezaghebbende leerboek van Landau en Lifshitz zegt dat "we alleen kunnen zeggen dat een bepaalde symmetrie-eigenschap bestaat of niet bestaat; ... Het kritieke punt kan daarom niet bestaan voor dergelijke fasen." Maar sinds 2001 de mogelijkheid van het vaste-vloeibare kritieke punt is gemeld in computersimulatiestudies van water in nanoporiën. In feite, er is geen rigoureus bewijs voor het niet-bestaan van het vaste-vloeibare kritieke punt.
Kenji Mochizuki en Kenichiro Koga van de Okayama University hebben ondubbelzinnig bewijs geleverd om het vaste-vloeistof-kritische punt voor een klasse water in nanobuisjes te ondersteunen door uitgebreide moleculaire dynamica-simulaties uit te voeren:macroscopische vaste-vloeistof-fasescheiding onder een kritische temperatuur Tc, divergerende warmtecapaciteit en isotherme samendrukbaarheid rond Tc, en de loci van responsfunctie maxima (de Widom-lijnen) boven Tc.
Figuur 1 toont de waterstofbrugstructuren van zes ijskristallen gevormd in koolstofnanobuisjes met een diameter van 1,11 nm en 1,25 nm. De onderzoekers ontdekten dat alle fasegrenzen van de eerste orde tussen het ijs en de vloeistof uiteindelijk ophielden te bestaan op de kritieke punten, zoals weergegeven in figuur 2. Het TP-fasediagram is heel anders dan dat van bulkwater, waar ijsgebieden volledig worden omringd door de fasegrenzen van de eerste orde (ononderbroken zwarte lijnen).
De onderzoekers gaven ook een microscopische verklaring voor een eenvoudige, nog onbeantwoord, vraag:hoe kan vloeibaar water continu bevriezen tot kristallijn ijs? Ze vonden dynamische fluctuaties van microscopisch kleine domeinen van water en ijs nabij het kritieke punt - een microscopisch beeld van water in de loop van geleidelijk bevriezen of smelten.
De kritische punten in beschut water zijn alomtegenwoordig en kunnen worden gevonden bij omgevingscondities door de poriediameter af te stemmen, en daarom is een van de mogelijke toepassingen om de afstembare kritische fluctuaties te gebruiken om chemische reacties te vergemakkelijken, structurele veranderingen in biologische moleculen, en vorming van assemblage van biomoleculen in water.
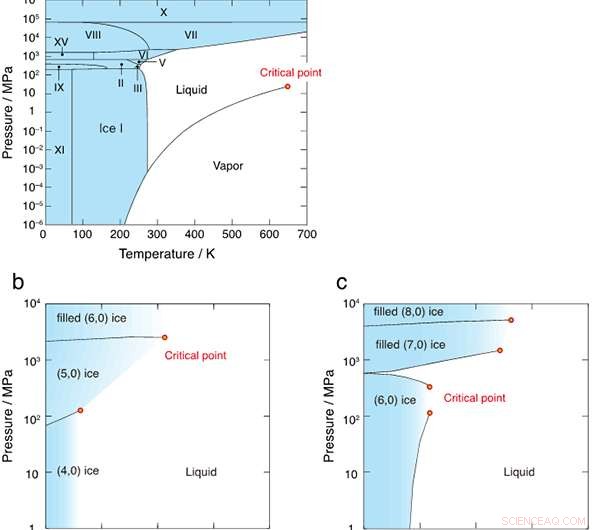
Figuur 2:Fasediagrammen van (a) bulkwater, (b) water opgesloten in de nanobuis met een diameter van 1,11 nm, en (c) 1,25 nm. De fasediagrammen van (b) en (c) worden eerst onthuld in deze studie. Vaste gebieden zijn blauw gekleurd en kritieke punten zijn aangegeven met rode cirkels.
 In de Gaslandse gemeenschap, nieuwe tests doen oud boordebat herleven
In de Gaslandse gemeenschap, nieuwe tests doen oud boordebat herleven Het leven herstelde zich snel op de inslagplaats van de dino-dodende asteroïde
Het leven herstelde zich snel op de inslagplaats van de dino-dodende asteroïde Ondergrondse glasvezelsensoren registreren geluiden van COVID-lockdown, heropening
Ondergrondse glasvezelsensoren registreren geluiden van COVID-lockdown, heropening Planten en dieren die van oorsprong afkomstig zijn uit Colombia
Planten en dieren die van oorsprong afkomstig zijn uit Colombia Bedreigde dieren: The Snowy Owl
Bedreigde dieren: The Snowy Owl
Hoofdlijnen
- Ziekteverwekkers identificeren die sojastamkanker veroorzaken
- Afrika stroperij nu een oorlog, taskforce waarschuwt
- De nadelen van gelelektroforese
- Elandenpopulatie in Vermont worstelt ondanks bezuiniging op jacht
- De rol van enzymen bij cellulaire ademhaling
- Honden snuffelden vroeger aan zeldzame soorten
- Processen die ATP gebruiken als energiebron
- Kwallen op het menu
- Hoe afnemende zoogdierpopulaties in de Florida Everglades verband houden met de invasieve Birmese python
- Een quantum dot energy harvester:afvalwarmte omzetten in elektriciteit op nanoschaal
- Proces voor het visualiseren van defecten in vaste kristallen, verbeterd door kunstmatige intelligentie

- Zilver valt bacteriën aan, wordt geconsumeerd

- Nieuwe nanopincet die objecten van submicrometergrootte in vloeistoffen kan verplaatsen
- Enkele atoomlaagval voor lithium-ionmigratie

 Onderzoekers ontwikkelen genetisch hulpmiddel om arseenstudies te verbeteren
Onderzoekers ontwikkelen genetisch hulpmiddel om arseenstudies te verbeteren Amerikaanse toezichthouders onder vuur Boeing lanceert charmeoffensief
Amerikaanse toezichthouders onder vuur Boeing lanceert charmeoffensief Amazon-werknemers van over de hele wereld bundelen hun krachten in Berlijn
Amazon-werknemers van over de hele wereld bundelen hun krachten in Berlijn Nieuw op metallo-enzymen gebaseerd systeem maakt selectieve targeting van kankercellen mogelijk
Nieuw op metallo-enzymen gebaseerd systeem maakt selectieve targeting van kankercellen mogelijk Bewoners keren terug naar door storm geteisterde Florida Keys
Bewoners keren terug naar door storm geteisterde Florida Keys Kleine technologie reinigt vuil water
Kleine technologie reinigt vuil water Facebook heeft (voorlopig) geen plannen om je gesprekken af te luisteren, maar de enge verhalen stapelen zich op
Facebook heeft (voorlopig) geen plannen om je gesprekken af te luisteren, maar de enge verhalen stapelen zich op Middelvingeroorlogen tussen wielrenners en coureurs:betreed het emoji-jasje
Middelvingeroorlogen tussen wielrenners en coureurs:betreed het emoji-jasje
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

