
Wetenschap
Wiskundigen kraken 44 jaar oud probleem

Tarski bewees dat een cirkel met een straal van één niet volledig kan worden bedekt door stroken waarvan de gecombineerde breedte kleiner is dan twee - de diameter van de cirkel. Elk van de stroken in de afbeelding heeft zijn eigen lengte en kleur. Krediet:MIPT
Israel Institute of Technology en Alexandr Polyanskii van het Moscow Institute of Physics and Technology (MIPT) hebben het zonevermoeden van László Fejes Tóth bewezen. Geformuleerd in 1973, er staat dat als een eenheidsbol volledig wordt bedekt door meerdere zones, hun gecombineerde breedte is minstens π. Het bewijs, gepubliceerd in het tijdschrift Geometrische en functionele analyse , is belangrijk voor discrete meetkunde en stelt wiskundigen in staat om nieuwe problemen te formuleren.
Discrete geometrie bestudeert de combinatorische eigenschappen van punten, lijnen, cirkels, veelhoeken en andere geometrische objecten. Wat is het grootste aantal ballen van gelijke grootte dat om een andere bal van dezelfde grootte kan? Wat is de dichtste manier om cirkels van gelijke grootte in een vlak te verpakken, of ballen in een bevattende ruimte? Deze en andere vragen worden beantwoord door discrete geometrie.
Oplossingen voor dit soort problemen hebben praktische toepassingen. Dus, het dichte verpakkingsprobleem heeft geholpen bij het optimaliseren van de codering en het corrigeren van fouten in de gegevensoverdracht. Een ander voorbeeld is de vierkleurenstelling, die zegt dat vier kleuren voldoende zijn om elke kaart op een bol te plotten, zodat geen twee aangrenzende regio's dezelfde kleur hebben. Het heeft wiskundigen ertoe aangezet om concepten te introduceren die belangrijk zijn voor de grafentheorie, die cruciaal is voor veel van de recente ontwikkelingen in de chemie, biologie en informatica, evenals logistieke systemen.
Het zonevermoeden van Tóth hangt nauw samen met een aantal andere problemen in discrete meetkunde die in de 20e eeuw werden opgelost met betrekking tot het bedekken van een oppervlak met stroken. De eerste daarvan was het zogenaamde plankenprobleem, waarbij een schijf werd bedekt met stroken begrensd door evenwijdige lijnen. Alfred Tarski en Henryk Moese boden een eenvoudig bewijs aan dat de gecombineerde breedte van deze stroken, of planken, mag de diameter van de schijf niet overschrijden. Dat is, er is geen betere manier om een schijf te bedekken dan met een enkele plank waarvan de breedte gelijk is aan de diameter van de schijf. Thøger Bang loste vervolgens het probleem op door een willekeurig convex lichaam met strips te bedekken. Namelijk, hij bewees dat de gecombineerde breedte van de stroken die een convex lichaam bedekken ten minste de breedte van het lichaam zelf is, dat is, de minimale breedte van een enkele strook die het lichaam bedekt.
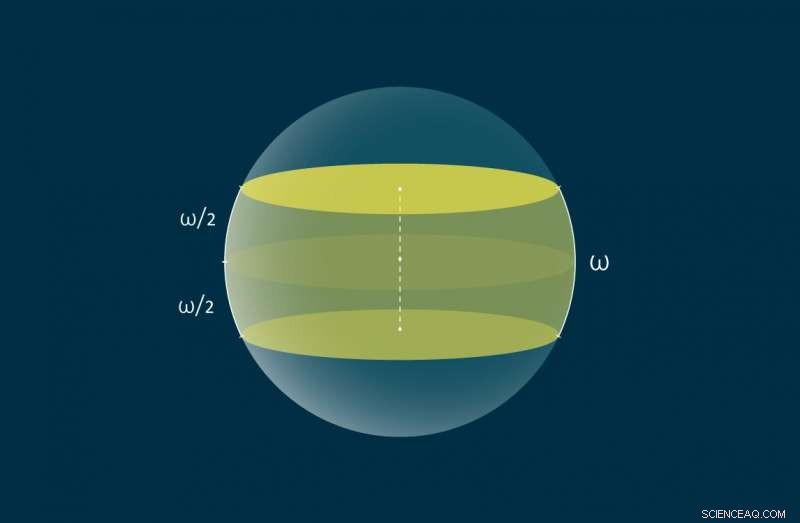
Een zone met de breedte ω op de bol is in geel weergegeven. Krediet:MIPT
Het probleem dat door de auteurs wordt aangepakt, is anders omdat het gaat om het bedekken van een eenheidsbol met speciaal geconstrueerde zones. specifiek, elke zone is de kruising van de bol met een bepaalde driedimensionale plank, waarbij een plank het ruimtegebied is tussen twee evenwijdige vlakken die symmetrisch zijn ten opzichte van het middelpunt van de bol. Alternatief, zones kunnen worden gedefinieerd in geodetische metrische ruimte zonder toevlucht te nemen tot planken:Een zone van breedte ω op het oppervlak van een eenheidsbol is de verzameling punten die niet verder dan ω/2 van de grootcirkel liggen, of evenaar, met de afstanden tussen punten gemeten als de kortste bogen die ze verbinden. De wiskundigen moesten de minimale gecombineerde breedte vinden van dergelijke zones die de eenheidsbol bedekken. Dus, het probleem verschilt van het eerder opgeloste probleem in de manier waarop de breedte wordt gemeten - het wordt gedefinieerd als de lengte van een boog, in plaats van de Euclidische afstand tussen evenwijdige lijnen of vlakken.
Het bewijs gepresenteerd door Jiang en Polyanskii was geïnspireerd door Bang, die het probleem oploste om een lichaam met stroken te bedekken door een speciale eindige reeks punten in het lichaam te vormen, waarvan er één zogenaamd niet door een van de strips werd bedekt. Op een manier, zowel Bang als de auteurs leveren een bewijs door tegenspraak. In het geval van het vermoeden van Fejes Tóth, de wiskundigen veronderstelden dat de gecombineerde breedte van zones die de bol volledig bedekken kleiner was dan π en probeerden tot een tegenstrijdigheid te komen, namelijk, vind een punt dat op de bol ligt, maar niet in een van de zones.
De auteurs hebben aangetoond dat het mogelijk is om een reeks punten in een driedimensionale ruimte te vormen, zodat ten minste één punt niet wordt bedekt door de planken die de zones vormen. Als deze hele verzameling in de bol ligt, het is dan relatief eenvoudig om een ander punt op de bol te plotten dat ook niet door de planken wordt bedekt, en dus door de zones. Als een van de punten in de set toevallig buiten de bol ligt, het blijkt mogelijk om één grotere zone te vervangen door meerdere kleinere, waarvan de gecombineerde breedte gelijk is aan die van de grotere zone. Dus, het is mogelijk om het aantal zones in het oorspronkelijke probleem te verminderen zonder hun gecombineerde breedte te beïnvloeden. Eventueel, een punt op de bol wordt geïdentificeerd dat niet door de zones wordt gedekt. Dit druist in tegen de hypothese dat de gecombineerde breedte van de zones kleiner is dan π, bewijst het vermoeden van Fejes Tóth.

Zones die een bol volledig bedekken. Elk van de vijf zones heeft zijn eigen breedte en kleur. Krediet:MIPT
Het probleem is opgelost in de n-dimensionale ruimte, maar de auteurs zeggen dat dit het niet anders maakt dan het geval met drie dimensies.
"Het probleem van Fejes Tóth fascineert wiskundigen al meer dan 40 jaar op het gebied van discrete meetkunde, " zegt auteur Alexandr Polyanskii van de afdeling Discrete Wiskunde, MIPT. "Dit probleem bleek een elegante oplossing te hebben, die we gelukkig konden vinden. Het probleem van Fejes Tóth bracht ons ertoe een ander probleem te overwegen, meer fundamenteel vermoeden over de bedekking van een bol door verschoven zones gedefinieerd als de kruising van de bol met driedimensionale planken die niet noodzakelijk centraal symmetrisch zijn."
 Gigantische doorbraak in flexo-elektriciteit in zachte elastomeren maakt de weg vrij voor verbeterde robots en zelfaangedreven pacemakers
Gigantische doorbraak in flexo-elektriciteit in zachte elastomeren maakt de weg vrij voor verbeterde robots en zelfaangedreven pacemakers Op zoek naar de meest effectieve polymeren voor persoonlijke beschermingsmiddelen
Op zoek naar de meest effectieve polymeren voor persoonlijke beschermingsmiddelen Van hard naar zacht:sponzen maken van mosselschelpen
Van hard naar zacht:sponzen maken van mosselschelpen Doel van titratie
Doel van titratie  OLED's worden helderder en duurzamer
OLED's worden helderder en duurzamer
 Koolstof volgen van het oceaanoppervlak naar de schemerzone
Koolstof volgen van het oceaanoppervlak naar de schemerzone De ongebruikelijke verbinding tussen bevers,
De ongebruikelijke verbinding tussen bevers,  Klei als voedingssupplement bij melkvee heeft meerdere voordelen
Klei als voedingssupplement bij melkvee heeft meerdere voordelen Wetenschappers onthullen onderzeese canyon aan de rand van het continentale plat van Ierland
Wetenschappers onthullen onderzeese canyon aan de rand van het continentale plat van Ierland Onderzoekers voorspelden een iets bovengemiddeld Atlantisch orkaanseizoen 2018
Onderzoekers voorspelden een iets bovengemiddeld Atlantisch orkaanseizoen 2018
Hoofdlijnen
- Ecologische successie: definitie, types, stadia en voorbeelden
- Inleiding tot hoe gigantische virussen werken
- Celmodellen voor wetenschapsprojecten
- Pharmacy Research Topics
- Gletsjermuizen bewegen en dat heeft wetenschappers versteld doen staan
- Hebben plantencellen flagella?
- Studie verlicht genetische oorsprong van diversiteit in huidskleur
- Internationale concurrentiebenchmarks metagenomics-software
- Vogelgriep:Nederlandse boeren moeten pluimvee binnen houden
- Vrouwelijke politieke leiders sleutel tot meer gelijke en zorgzame samenlevingen

- Moeten we ons zorgen maken dat de helft van de Amerikanen op hun gevoel vertrouwt om hen te vertellen wat waar is?

- Wat zijn de Nazca-lijnen?

- Nobelprijsuitreikingen opnieuw ingekort vanwege pandemie

- Robin de robot helpt zieke kinderen zich minder eenzaam te voelen
 Het pad voor cellen verlichten
Het pad voor cellen verlichten NASA's infrarood blik op orkaan Gert
NASA's infrarood blik op orkaan Gert NASA ziet tropische cycloon 33W verdwijnen
NASA ziet tropische cycloon 33W verdwijnen Nanotechnologie-onderzoekers ontwikkelen nieuwe strategie om chemotherapie aan prostaatkankercellen te leveren
Nanotechnologie-onderzoekers ontwikkelen nieuwe strategie om chemotherapie aan prostaatkankercellen te leveren Röntgenmicroscopie 10 keer sneller maken
Röntgenmicroscopie 10 keer sneller maken Methode om de niveaus van ozonvervuiling aan het oppervlak te voorspellen, geeft een waarschuwing binnen 48 uur
Methode om de niveaus van ozonvervuiling aan het oppervlak te voorspellen, geeft een waarschuwing binnen 48 uur Hoe vloeistofviscositeit de intensiteit van aardbevingen beïnvloedt
Hoe vloeistofviscositeit de intensiteit van aardbevingen beïnvloedt Hoe onze universele plastic tragedie op te ruimen?
Hoe onze universele plastic tragedie op te ruimen?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

