
Wetenschap
Volgens de wet van zwaartekracht, hoe relateert de zwaartekracht een objecten afstand van het centrum van de aarde?
In de context van de aarde betekent dit:
* Terwijl een object verder weg van het centrum van de aarde beweegt, neemt de zwaartekracht. af. De kracht wordt zwakker met een snelheid die evenredig is met het kwadraat van de afstand.
* Als u de afstand van het centrum van de aarde verdubbelt, neemt de zwaartekracht af tot een vierde zijn oorspronkelijke waarde.
* Als u de afstand verdrievoudigt, neemt de zwaartekracht af tot één negende zijn oorspronkelijke waarde.
Deze relatie wordt wiskundig uitgedrukt als:
f =g * (m1 * m2) / r²
Waar:
* f is de kracht van de zwaartekracht
* g is de zwaartekrachtconstante (een universele waarde)
* M1 is de massa van de aarde
* m2 is de massa van het object
* r is de afstand tussen de centra van de aarde en het object
Daarom verzwakt de zwaartekracht aanzienlijk met toenemende afstand van het centrum van de aarde. Dit is de reden waarom astronauten gewichtloosheid in de ruimte ervaren, omdat ze ver van het centrum van de aarde zijn.
 Baanbrekende kwantumchemietechniek voor computationeel ontwerp en optimalisatie van organische fotofunctionele materialen
Baanbrekende kwantumchemietechniek voor computationeel ontwerp en optimalisatie van organische fotofunctionele materialen Wanneer radioactief fosfor vervalt, zendt het een positron uit. Zal de resulterende kern een andere isotoop van fosfor zijn?
Wanneer radioactief fosfor vervalt, zendt het een positron uit. Zal de resulterende kern een andere isotoop van fosfor zijn?  Röntgenlaserwetenschappers ontwikkelen een nieuwe manier om te zien hoe bacteriën antibiotica aanvallen
Röntgenlaserwetenschappers ontwikkelen een nieuwe manier om te zien hoe bacteriën antibiotica aanvallen Welk gas voldoet aan de wetten op alle omstandigheden van temperatuur en druk?
Welk gas voldoet aan de wetten op alle omstandigheden van temperatuur en druk?  Welk wetenschappelijk hulpmiddel wordt gebruikt om de boel in een laboratorium op te warmen?
Welk wetenschappelijk hulpmiddel wordt gebruikt om de boel in een laboratorium op te warmen?
Hoofdlijnen
- Volgens de evolutietheorie, hoe zijn mensen en verwant?
- Relatie tussen DNA en natuurlijke selectie
- Wat zijn vier theorieën die de oorsprong van een staat verklaren?
- Vang me als je kunt:hoe mRNA-therapieën in cellen worden afgeleverd
- Sommige planten kunnen de toxische effecten van metalen kortsluiten. Nu proberen wetenschappers hun kracht te benutten
- Wat zijn de nadelen van een plantencel?
- Welke individuen hebben gelijktijdig evolutiemechanismen beschreven?
- Is er een gen voor de menselijke geest?
- Geeft klonen u een exacte replica?
- Atoombiljart met röntgenstralen:een nieuwe benadering om in moleculen te kijken

- Een nieuwe richting van topologisch onderzoek staat klaar om van de grond te komen

- Verbeterde interacties door sterke licht-materie koppeling
- Nieuwe halfgeleiderdetector veelbelovend voor medische diagnostiek en binnenlandse veiligheid

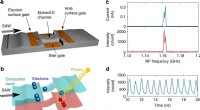
- Het produceren van enkele fotonen uit een stroom van enkele elektronen
 Tencent gaat ID's controleren om spellimieten voor minderjarigen af te dwingen
Tencent gaat ID's controleren om spellimieten voor minderjarigen af te dwingen Wat is de uitvoering van evolutie?
Wat is de uitvoering van evolutie?  Nieuwe tijdlijn van dodelijkste bosbrand in Californië kan levensreddend onderzoek en actie leiden
Nieuwe tijdlijn van dodelijkste bosbrand in Californië kan levensreddend onderzoek en actie leiden Hoe kunt u de oplosbaarheid van een opgeloste stof veranderen?
Hoe kunt u de oplosbaarheid van een opgeloste stof veranderen?  Waarom gebruiken wetenschappers het model om atomen weer te geven?
Waarom gebruiken wetenschappers het model om atomen weer te geven?  Hoeveel ongepaarde elektronen heeft silicium en lithium?
Hoeveel ongepaarde elektronen heeft silicium en lithium?  Onderzoekers berekenen hoe riviernetwerken zich door een landschap bewegen
Onderzoekers berekenen hoe riviernetwerken zich door een landschap bewegen  Een verandering in energie van de ene vorm naar de andere is?
Een verandering in energie van de ene vorm naar de andere is?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

