
Wetenschap
Onderzoeksteam stelt synthetische dimensiedynamiek vast om licht te manipuleren
Op het gebied van de natuurkunde zijn synthetische dimensies (SD's) naar voren gekomen als een van de grenzen van actief onderzoek, en bieden ze een pad om fenomenen in hoger-dimensionale ruimtes te verkennen, buiten onze conventionele 3D-geometrische ruimte. Het concept heeft veel aandacht gekregen, vooral in de topologische fotonica, vanwege het potentieel om rijke natuurkunde te ontsluiten die in traditionele dimensies ontoegankelijk is.
Onderzoekers hebben verschillende theoretische raamwerken voorgesteld om SD's te bestuderen en te implementeren, met als doel fenomenen als synthetische ijkvelden, quantum Hall-fysica, discrete solitonen en topologische fase-overgangen in vier dimensies of hoger te benutten. Deze voorstellen zouden kunnen leiden tot nieuwe fundamentele inzichten in de natuurkunde.
Een van de belangrijkste uitdagingen in de conventionele 3D-ruimte is de experimentele realisatie van complexe roosterstructuren met specifieke koppelingen. SD's bieden een oplossing door een toegankelijker platform te bieden voor het creëren van ingewikkelde netwerken van resonatoren met anisotrope, langeafstands- of dissipatieve koppelingen. Deze mogelijkheid heeft al geleid tot baanbrekende demonstraties van niet-hermitische topologische windingen, pariteit-tijd-symmetrie en andere verschijnselen.
Een verscheidenheid aan parameters of vrijheidsgraden binnen een systeem, zoals frequentiemodi, ruimtelijke modi en orbitale hoekmomenten, kunnen worden gebruikt om SD's te construeren, wat veelbelovend is voor toepassingen in diverse velden, variërend van optische communicatie tot topologische isolatorlasers.
Een belangrijk doel op dit gebied is de constructie van een ‘utopisch’ netwerk van resonatoren waarin elk paar modi op een gecontroleerde manier kan worden gekoppeld. Om dit doel te bereiken is nauwkeurige modusmanipulatie binnen fotonische systemen nodig, wat mogelijkheden biedt voor het verbeteren van de datatransmissie, de efficiëntie van het oogsten van energie en de uitstraling van laserarrays.

Nu, zoals gerapporteerd in Advanced Photonics heeft een internationaal team van onderzoekers aanpasbare arrays van golfgeleiders gemaakt om synthetische modale dimensies vast te stellen. Deze vooruitgang maakt effectieve controle van licht in een fotonisch systeem mogelijk, zonder de noodzaak van ingewikkelde extra functies zoals niet-lineariteit of niet-hermiticiteit.
Professor Zhigang Chen van de Nankai Universiteit merkt op:"Het vermogen om verschillende lichtmodi binnen het systeem aan te passen brengt ons een stap dichter bij het realiseren van 'utopische' netwerken, waarin alle parameters van een experiment perfect controleerbaar zijn."
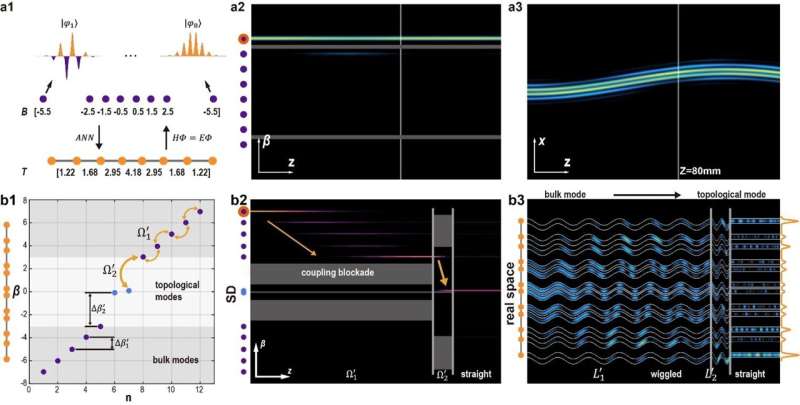
In hun werk moduleren de onderzoekers verstoringen ("wiebelfrequenties") voor voortplantingen die overeenkomen met de verschillen tussen verschillende lichtmodi. Om dit te doen, gebruiken ze kunstmatige neurale netwerken (ANN's) om golfgeleiderarrays in de echte ruimte te ontwerpen. De ANN's zijn getraind om golfgeleideropstellingen te maken die precies de gewenste moduspatronen hebben. Deze tests helpen onthullen hoe licht zich voortplant en binnen de arrays wordt opgesloten.
Ten slotte demonstreren de onderzoekers het gebruik van ANN's om een speciaal type fotonische roosterstructuur te ontwerpen, een Su-Schrieffer-Heeger (SSH) rooster. Dit rooster heeft een specifieke eigenschap die topologische controle van het licht door het hele systeem mogelijk maakt. Hierdoor kunnen ze de bulkmodus waarin licht zich verplaatst veranderen, waardoor de unieke eigenschappen van hun synthetische dimensies worden benadrukt.
De implicaties van dit werk zijn aanzienlijk. Door de afstanden en frequenties van de golfgeleiders nauwkeurig af te stemmen, willen de onderzoekers het ontwerp en de fabricage van geïntegreerde fotonische apparaten optimaliseren.
Professor Hrvoje Buljan van de Universiteit van Zagreb zegt:"Naast fotonica biedt dit werk een kijkje in de geometrisch ontoegankelijke natuurkunde. Het is veelbelovend voor toepassingen variërend van mode-lasing tot kwantumoptica en datatransmissie."
Zowel Chen als Buljan merken op dat het samenspel van topologische fotonica en fotonica met synthetische dimensies, mogelijk gemaakt door ANN's, nieuwe mogelijkheden opent voor ontdekkingen die kunnen leiden tot ongekende materialen en apparaattoepassingen.