
Wetenschap
Wiskunde gebruiken om de spinovergang tussen de assemblage van vezels in garen te beschrijven
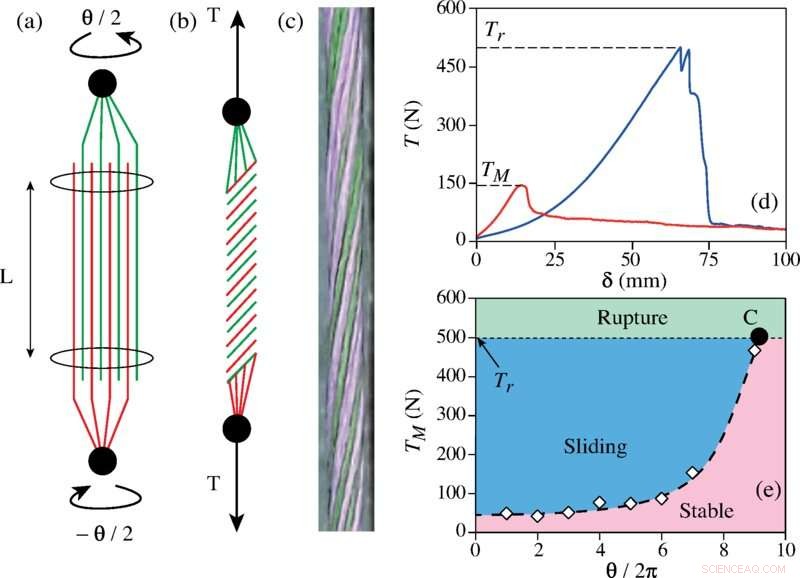
Krediet:Fysieke beoordelingsbrieven (2022). DOI:10.1103/PhysRevLett.128.078002
Een paar onderzoekers van respectievelijk de Université Paris-Saclay, CNRS en Univ Rennes, CNRS, IPR, hebben wiskunde gebruikt om het proces te beschrijven dat betrokken is wanneer korte vezelstrengen in lange stukken garen worden gedraaid. In hun paper gepubliceerd in het tijdschrift Physical Review Letters, Antoine Seguin en Jérôme Crassous beschrijven hoe ze experimenten en simulaties gebruikten om de factoren die betrokken zijn bij het in elkaar draaien van vezels beter te begrijpen.
Mensen hebben al duizenden jaren korte vezelstrengen in elkaar gedraaid om lange strengen touw of garen te maken, en hoewel het algehele proces goed wordt begrepen, was de wiskunde erachter nogal schetsmatig. In deze nieuwe poging hebben Seguin en Crassous het probleem aangepakt met een nieuwe aanpak, waarbij zowel experimenten als simulaties zijn toegepast.
Doordat meerdere korte vezels in elkaar gedraaid zijn, raken ze verstrengeld, maar dat is natuurlijk niet genoeg om ze bij elkaar te houden. Ze houden elkaar vast vanwege de wrijving die ermee gepaard gaat. Trekken aan de uiteinden van een stuk garen dwingt de afzonderlijke strengen waarvan het is gemaakt in elkaar te duwen, waardoor de hoeveelheid wrijving en daarmee de sterkte toeneemt. Maar zijn er wiskundige regels die het proces beheersen? Wat is bijvoorbeeld het optimale aantal vezels om het sterkste garen te krijgen? Of welke mate van sterkte wordt aan het garen gegeven door de mate van wrijving tussen twee vezelstrengen?
Om deze antwoorden te vinden, voerden de onderzoekers meerdere tests uit op verschillende vezels die tot garens waren gedraaid. Ze ontdekten dat een toename van het aantal wendingen de sterkte van de vezelbinding verhoogde, maar slechts tot op zekere hoogte. Ook had elk type vezel zijn eigen breekpunt. Bij het maken van simulaties om gemakkelijker verschillende configuraties te testen, ontdekten ze ook dat er een optimale vezelradius was voor een gegeven garenlengte en dat de garensterkte werd geschaald met het exponentiële kwadraat van de draaihoek.
Bij het zoeken naar overeenkomsten ontdekten ze wat ze het Hercules-twistgetal noemen - een parameter die de krachten beschrijft die betrokken zijn bij de draaihoek, een wrijvingscoëfficiënt en de straal van het garen. Ze ontdekten ook dat dit getal in het algemeen evenredig was met het kwadraat van het aantal toegepaste wendingen, en een kritische waarde van 30 had. Ze ontwikkelden ook een formule om de optimale straalgrootte voor een bepaald type vezel weer te geven. + Verder verkennen
Onderzoekers onderzoeken 'waarom kleding niet uit elkaar valt'
© 2022 Science X Network
 Een type semi-transparant polymeer dat bij kamertemperatuur kan worden hersteld met een kleine druk
Een type semi-transparant polymeer dat bij kamertemperatuur kan worden hersteld met een kleine druk Polyproline beschermt celmonolagen tegen vorstschade
Polyproline beschermt celmonolagen tegen vorstschade Barium Nitrate & Sodium Sulphate
Barium Nitrate & Sodium Sulphate Waarom wordt een zilveren ketting zwart?
Waarom wordt een zilveren ketting zwart?  Hoe maken we waterstof uit steenkool, en is het echt een schone brandstof?
Hoe maken we waterstof uit steenkool, en is het echt een schone brandstof?
Hoofdlijnen
- Revolutionaire microscoop- en labeltechniek brengt DNA-mutaties in kaart
- Onder het zee-ijs, aanschouw de oude Arctische kwallen
- DNA-bewijs onthult twee vergeten Noord-Amerikaanse migraties
- Nucleïnezuren: structuur, functie, typen en voorbeelden
- Het gebruik van pinguïns om de gezondheid van de oceaan te monitoren is mogelijk niet effectief
- Hoe toont hemoglobine de vier niveaus van eiwitstructuur?
- Hoe beïnvloeden allelen inherente eigenschappen?
- Namen van de enzymen in de mond & slokdarm
- Batesiaanse mimiek:hoe copycats zichzelf beschermen
- Voordelen en nadelen van hydrostatisch skelet

- Multifunctionele metalens ontgrendelt met licht
- Verstrooid licht gebruiken om kruispunten van zenuwvezelpaden in de hersenen in kaart te brengen
- Hoe verplaatst elektriciteit zich van de windturbine naar de bedrijven en gemeenschappen die het kopen?

- Stijgt een ballon met helium hoger dan één met zuurstof?

 Hoe maak je een Island School Project
Hoe maak je een Island School Project  3D-modellen van goedkope videocamera's
3D-modellen van goedkope videocamera's De oudste geologische afdrukken van de manen bestuderen
De oudste geologische afdrukken van de manen bestuderen Molecuul-plasmon koppelingssterkte stemt oppervlakte-verbeterde infrarode absorptie spectrale lijnvormen af
Molecuul-plasmon koppelingssterkte stemt oppervlakte-verbeterde infrarode absorptie spectrale lijnvormen af Methoden voor grote eiwitkristalgroei voor neutroneneiwitkristallografie
Methoden voor grote eiwitkristalgroei voor neutroneneiwitkristallografie Vergeten hoekje van Europa weer tot leven gebracht dankzij kunstmatige intelligentie
Vergeten hoekje van Europa weer tot leven gebracht dankzij kunstmatige intelligentie Winnaars van de wedstrijd:Apple kiest de beste foto's die met de iPhone zijn gemaakt
Winnaars van de wedstrijd:Apple kiest de beste foto's die met de iPhone zijn gemaakt Wetenschapper aan het werk:foto's maken op atomaire schaal van kleine kristallen, gebruik een enorme, kilometer lange synchrotron
Wetenschapper aan het werk:foto's maken op atomaire schaal van kleine kristallen, gebruik een enorme, kilometer lange synchrotron
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

