
Wetenschap
Kinematica van uitgerekte platen
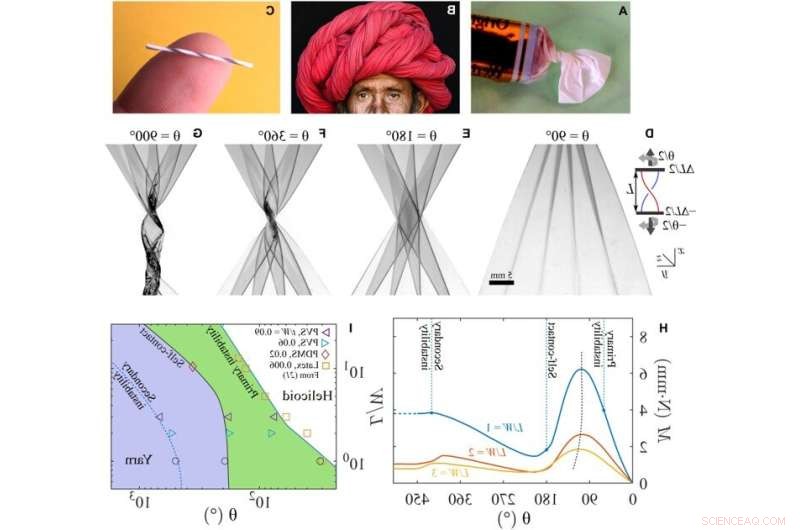
Experimenten onthullen een zeer geordende transformatie naar garens wanneer vellen die onder spanning worden gehouden, worden gedraaid voorbij het begin van primaire instabiliteiten. Voorbeelden van gedraaide, gevouwen en gekrulde structuren zijn de volgende:(A) verpakt snoep, (B) multifunctionele Rajashtani-tulband (fotocredit:Lauren Cohen) en (C) gerold garen van een polyethyleenvel (zie sectie S4). (D tot G) Shadowgraphs van een transparant PDMS-blad gedraaid door hoek θ zoals weergegeven in de inzet (L/W =1; t/W =0,0028; ΔL/L =0,1; θp =60 ± 5 °). Inzet:Schematisch en laboratoriumcoördinatensysteem. (D) Rimpels waargenomen net boven het begin van primaire instabiliteit. (E) Accordeon gevouwen blad met zelfcontact. (F) Een geneste helicoïde met gevouwen lagen die zich ontwikkelen naarmate het vel verder wordt gedraaid. (G) Secundaire knikinstabiliteit treedt op bij verder draaien, wat resulteert in een garenachtige structuur. De schaalbalk is hetzelfde in (D) tot (G). (H) Het gemeten koppel toont een herhaalde toenemende en afnemende zaagtandvariatie met twist. De amplitude van variatie neemt toe naarmate L/W afneemt. (I) Een kaart die regio's afbakent waar de primaire instabiliteit, zelfcontact en secundaire instabiliteit optreden als een functie van beeldverhouding en draaiing. Lijnen zijn gidsen voor het oog, behalve de primaire instabiliteit voor L/W> 3. Credit:Science Advances (2022). DOI:10.1126/sciadv.abi8818
In een nieuwe studie die nu is gepubliceerd als een rapport en ook geïllustreerd als de online voorpagina van Science Advances , Julien Chopin, Arshad Kudrolli en een onderzoeksteam in de natuurkunde in de VS en Brazilië toonden aan hoe gedraaide hyperelastische vellen meerlagige zelfgekrulde garens vormden. Door dominant rekken te integreren met vouwkinematica, maten ze koppel en energie afkomstig van geometrische niet-lineariteiten. Vervolgens introduceerden ze een geometrisch model om de vorming en structuur van dergelijke zelfgekrulde garens te verklaren. De resultaten toonden aan hoe een simpele draai van origami in het spanraam-twist-vouwraamwerk leidde tot de transformatie van rekbare vellen in zelf-geassembleerde architecturen.
Vormtransformatie van bladen
Traditioneel kunnen draaiende lakens functionele garens vormen die afhankelijk zijn van millennia van menselijke oefening om catgut-boogkoorden, chirurgische hechtingen en stoffen wearables te vormen; de praktijk mist echter nog steeds overkoepelende principes die de complexiteit van dergelijke architecturen leiden. Gescrollde garens met geneste structuren kunnen worden gebruikt om energie op batterijen te benutten en bij het inbedden van amorfe materialen. Spanningsvouwvouwen kan vlakke platen transformeren in gelaagde structuren via externe grensregulering. Draaivouwen en scrollen kunnen worden gebruikt om platte vellen opnieuw te configureren en opnieuw te gebruiken, zoals te zien is bij de multifunctionele Rajasthan-tulband.
Om vormtransformatie van vellen en het samenspel tussen topologie en grote vormtransformaties te begrijpen, gebruikten Chopin et al driedimensionale röntgenscanning om de spontane vorming van gedraaide, meerlagige garens met geordende interne architecturen te detailleren. Het is echter nog steeds een uitdaging om de grote vormtransformaties en configuraties te modelleren. Recente studies hebben elastische plaatmodellen opgenomen, waaronder de Föppl-von Kármán (FvK) -vergelijking om de initiële groei boven het begin van primaire instabiliteit op te lossen, maar dergelijke methoden blijven om de transformatie van een vlakke plaat in opgerolde garens te verklaren. In dit werk ontwikkelden Chopin et al een nieuw raamwerk om de kinematica van gestructureerde vellen te combineren, en gebruikten ze origami om deze waarnemingen te verklaren. Het team liet zien hoe de gevouwen vellen regelmatige veelhoekige vormen vertoonden zoals beschreven door Schläfli-symbolen en hoe origami-kinematica de belangrijkste kenmerken van de structuur vastlegde om een raamwerk te bieden dat diende als een gids voor het ontwikkelen van hyperelastische materialen met brede toepassingen.
Online omslag:Een dun polydimethylsiloxaan (PDMS) vel wordt gedraaid tot meerlagig gerold garen. Al millennia lang hebben mensen rekbare lakens gedraaid om functionele garens te vormen om kledingstukken, snaarinstrumenten en upcycle plastic te maken. Chopin en Kudrolli ontwikkelen een elasto-geometrisch raamwerk om de fysieke mechanismen te begrijpen die betrokken zijn bij het draaien van rekbare platen tot zelf-geassembleerde architecturen voor geavanceerde productiestrategieën. Krediet:Wetenschappelijke vooruitgang (2022). DOI:10.1126/sciadv.abi8818
Het team toonde voorbeelden van polydimethylsiloxaan (PDMS) platen met toenemende twist. Naarmate de toegepaste twist verder toenam, merkten ze de vorming van een geneste spiraalvormige structuur in de taille op, gevolgd door secundaire instabiliteiten en resulterend recursief vouwen en een gekruld meerlagig garen. Elke belangrijke vormtransformatie zorgde ervoor dat de veranderingssnelheid van het toegepaste koppel van teken veranderde en een zaagtandvariatie vormde met een draai.
Chopin et al. illustreerden het spanningsverdraaiingsraamwerk om de waargenomen hoofdfasen van transformatie van een vlakke plaat in zelfgewalste garens te begrijpen. Ze bereikten dit door een reeks modellen te introduceren om geometrie, elasticiteit en kinematica te combineren om vervolgens de waargenomen vormtransformaties vast te leggen. De onderzoekers legden de opgeslagen elastische energie en torsierespons vast en volgden dit werk met 3D-röntgentomografie om gedraaide polyvinylsiloxaan (PVS) -platen te reconstrueren. De wetenschappers berekenden vervolgens de buigenergiedichtheid met behulp van platen met verschillende Young's moduli en karakteriseerden de overdracht met twist.
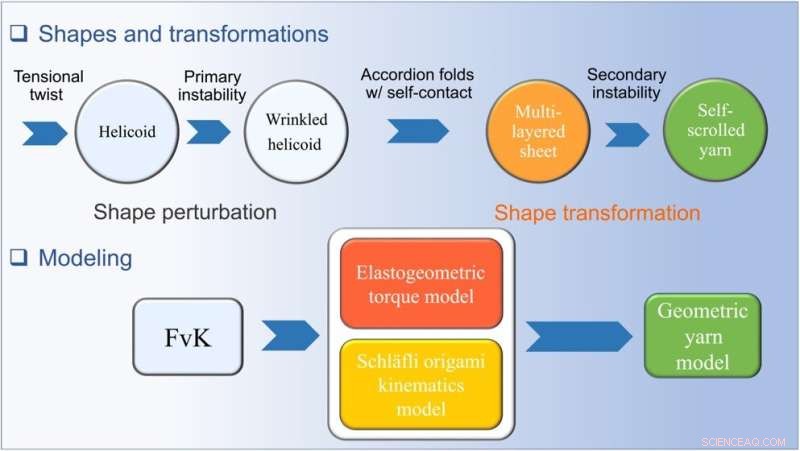
Een overzicht van de waarnemingstransformaties met twist en het tensional twist-folding raamwerk. De waargenomen hoofdtransformaties als een vlakke plaat ervaren gespannen twist-vouwen en scrollen met toegepaste twist. Het elastogeometrische raamwerk wordt getoond, inclusief het perturbatieve FvK-formalisme, het elastogeometrische koppelmodel dat geometrische niet-lineariteiten bevat om de spanning-rekrelatie met twist te verklaren, het Schläfli-origami-kinematische model en het geometrische garenmodel. Krediet:Wetenschappelijke vooruitgang (2022). DOI:10.1126/sciadv.abi8818
Elastogeometrisch koppelmodel, zelfvouwend en Schläfli-origami
Op basis van de experimentele waarnemingen ontwikkelden Chopin et al een elastogeometrisch model om de opgeslagen elastische energie en torsierespons van de plaat te berekenen. Ze bereikten dit door inspiratie te putten uit de spanningsveldentheorie om sterk gerimpelde platen te beschrijven, waar buig- en drukspanningen verwaarloosbaar waren in vergelijking met trekstrengen. Net als in de spanningsveldentheorie gingen Chopin et al ervan uit dat de energie tijdens het vouwen voornamelijk wordt gegeven door rekmodi in de lengterichting, terwijl de buigmodi subdominant waren. Het team vergeleek het gemeten koppel als een functie van de draaiing ten opzichte van de hyperelastische aard van het materiaal en vulde hun elastogeometrische analyse aan met origami-constructie om een goede overeenkomst tussen de origamivorm en het gedraaide vel aan te tonen. De wetenschappers identificeerden deze origami vervolgens met behulp van Schläfli-symbolen, die ze vervolgens Schläfli-origami noemden. Door de Schläfli-symbolen te variëren, verkregen Chopin et al. driehoekige, vijfhoekige, zevenhoekige en niet-hoekige enveloppen. Het werk benadrukte hoe de kinematica van origami ten grondslag lag aan het vouwen van de spanning.
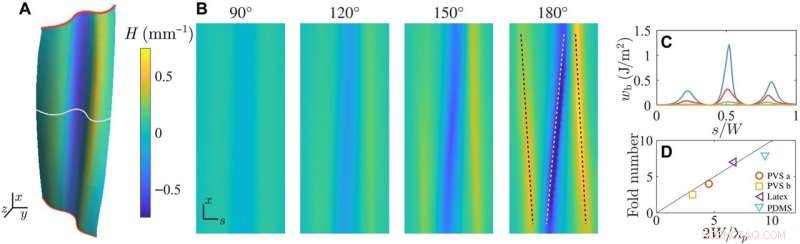
Accordeon vouwen door kromming lokalisatie. (A) De vervorming van een polyvinylsiloxaan (PVS)-plaat gedraaid met θ =120 ° verkregen met röntgentomografie en weergegeven met gemiddelde kromming H gegeven door de kleurenbalk aan de rechterkant (L/W =3; t/W =0,009; θp =75° ± 5°). De middelste 80% van de plaat verwijderd van de klemmen wordt weergegeven. (B) De ruimtelijke verdeling H toegewezen aan een rechthoekig domein toont symmetriebreking en lokalisatie van de bladkromming met twist. (C) Buiginhoud wb toont de lokalisatie van energie met vouwen over de dwarsdoorsnede aangegeven door de ononderbroken witte lijn in (A). (D) Het gemeten aantal vouwen n vergeleken met de relatie gegeven door de golflengte van de primaire instabiliteit n =2W/λp. De aspectverhoudingen (t/W, L/W) zijn als volgt:PVS a (0,009,2), PVS b (0,006,3), PDMS (0,003,1) en latex (0,003,2). De drie materialen zijn hyperelastisch met Young's modulus E =1,2 MPa (PVS), 6,2 MPa (PDMS) en 3,6 MPa (latex). Krediet:Wetenschappelijke vooruitgang (2022). DOI:10.1126/sciadv.abi8818
Garenvorming en het geometrische garenmodel
Om garengroei te modelleren, gingen Chopin et al ervan uit dat het vel in drie secties kon worden verdeeld, met een garenachtige structuur van lengte en twee waaierachtige structuren. Door deze vereenvoudiging konden ze de fundamentele rol van de gedraaide plaatrand in het elastogeometrische koppelmodel behouden. Ze bestudeerden ook de evolutie van de garenlengte door de waaierranden spiraalvormig rond een cilindrische kern met een specifieke diameter te wikkelen om uiteindelijk een groeimodel te vormen dat goed overeenkomt met de experimentele gegevens.
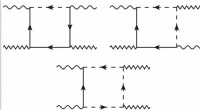
Gedeeltelijke Schläfli-origami verklaart gelaagde architecturen met een halve draai. (A) Geometrische vormen verkregen door het verhogen van de Schläfli-symbolen en het aantal facetten. (B) Vergelijking van het experimentele radiogram en Schläfli fold origami. In alle vier de gevallen wordt een goede correspondentie waargenomen. (C) De hoek Ψi van de i-de vouw als functie van de berekende hoek i α met behulp van het geometrische model komt uitstekend overeen. (D) Vergelijking van de tophoek α als functie berekend α met behulp van verschillende vellen en laden. (E) De tophoek als functie van het driehoeksgetal is in wezen constant. Krediet:Wetenschappelijke vooruitgang (2022). DOI:10.1126/sciadv.abi8818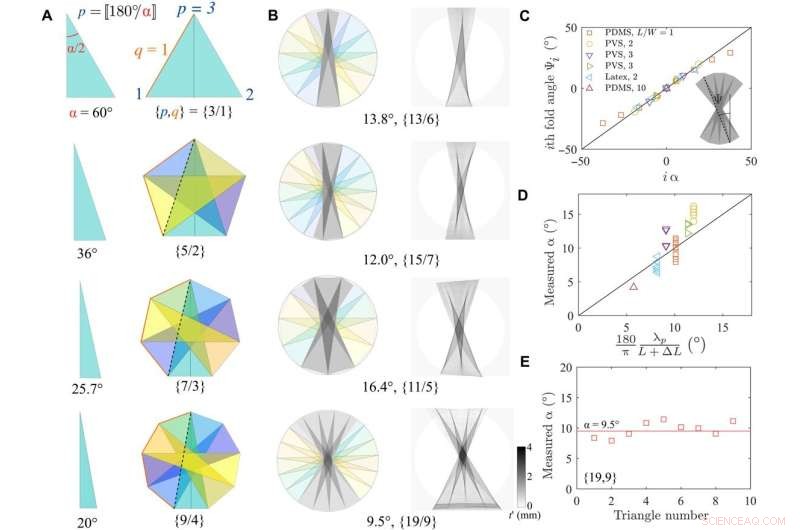
Op deze manier beschreven Julien Chopin, Arshad Kudrolli en collega's de opmerkelijk geordende transformatie van platte vellen naar gekrulde meerlagige garens. Ze bereikten dit door een reeks vereenvoudigde elastogeometrische modellen te introduceren om een spanraamwerk te vormen. Het team verkende de platte meerlagige structuur door een Schläfli-origamimodel te introduceren, waarbij de origami, wanneer gedraaid door een halve draai, regelmatige stervormige polygonen vormde die worden gekenmerkt door Schläfli-symbolen. Chopin et al. gebruikten röntgentomografie-analyse om de evolutie van het vel te verklaren en gaven de samenstelling aan van een sterk gedraaid garengebied in het midden en zwak gedraaide waaierachtige gebieden verbonden met de twee klemmen. Het model dat in dit werk is verwerkt, was gebaseerd op vereenvoudigde kinematica om een raamwerk te bieden om multifunctionele garens mogelijk te maken met behulp van ultradunne polymeren, koolstofnanobuizen en grafeenvellen, geschikt als materialen met toepassingen in de geneeskunde en flexibele elektronica. De wetenschappers gebruikten PDMS (polydimethylsiloxaan) en PVS (polyvinylsiloxaan) polymeren vanwege hun hyperelasticiteit onder verschillende belastingsomstandigheden. De resulterende twist-folding-strategie kan her-inzetbare functionele structuren creëren van eenvoudige elementen voor geavanceerde fabricage met zachte materialen. + Verder verkennen
Wiskunde gebruiken om de spinovergang tussen de assemblage van vezels in garen te beschrijven
© 2022 Science X Network
 Lijst van pitloze vasculaire planten
Lijst van pitloze vasculaire planten Hoe lieten dinosaurussen sporen achter in massieve steen?
Hoe lieten dinosaurussen sporen achter in massieve steen?  Huis keurt wetgeving goed om chemische verontreiniging met PFAS aan te pakken
Huis keurt wetgeving goed om chemische verontreiniging met PFAS aan te pakken Wetenschappers vinden verrassend bewijs van snelle veranderingen in het noordpoolgebied
Wetenschappers vinden verrassend bewijs van snelle veranderingen in het noordpoolgebied Nieuwe studie daagt de heersende theorie uit over hoe diepzee-openingen worden gekoloniseerd
Nieuwe studie daagt de heersende theorie uit over hoe diepzee-openingen worden gekoloniseerd
Hoofdlijnen
- Kan een naaimachine DNA aan elkaar naaien?
- Poema's zijn socialer dan eerder werd gedacht
- Eerste mycobiome-atlas beschrijft associaties tussen kanker en schimmels
- Niet-vasculaire plant: definitie, kenmerken, voordelen en voorbeelden
- De oorsprong van genen voor het maken van bloemen
- Hoe doodt alcohol bacteriën?
- Voor het eerst hebben wetenschappers levende bacteriën rechtstreeks waargenomen in poolijs en sneeuw
- Ondiepwaterwinning is geen duurzaam alternatief voor diepwaterwinning, beweren wetenschappers
- Genomische kenmerken verklaard door bepaalde kenmerken van de levensgeschiedenis bij neoaviaire vogels
- Studie onthult nieuwe supersymmetrie-anomalieën in superconforme kwantumveldentheorieën
- Standaardmodel van het universum doorstaat de meest nauwkeurige test van Dark Energy Survey (update)

- Zoeken naar axion-conversiesignalen voor donkere materie in de magnetische velden rond neutronensterren

- Meta-spiegel weerkaatst geluidsgolven in elke richting

- Multifunctionele elektrostatische druppelpincet begeleidt op afstand de druppelbeweging

 Een 4G-netwerk op de maan is slecht nieuws voor radioastronomie
Een 4G-netwerk op de maan is slecht nieuws voor radioastronomie Onderzoek heeft tot doel tweetalige leerders begrijpend lezen te stimuleren
Onderzoek heeft tot doel tweetalige leerders begrijpend lezen te stimuleren Wetenschapper ontdekt nieuwe oxidatietoestand van rhodium
Wetenschapper ontdekt nieuwe oxidatietoestand van rhodium NASA vindt kommavorm van tropische storm Wukong
NASA vindt kommavorm van tropische storm Wukong Earth-monitoring Landsat 9-satelliet gelanceerd in Californië
Earth-monitoring Landsat 9-satelliet gelanceerd in Californië Nieuw onderzoek documenteert de ernst van LGBTQA+-conversiepraktijken - en waarom vertrouwen belangrijk is bij herstel
Nieuw onderzoek documenteert de ernst van LGBTQA+-conversiepraktijken - en waarom vertrouwen belangrijk is bij herstel Nieuwe studie biedt inzicht in een hondenleven in gezinnen met kinderen
Nieuwe studie biedt inzicht in een hondenleven in gezinnen met kinderen Groenere chemie door nieuwe benadering van katalyse
Groenere chemie door nieuwe benadering van katalyse
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

