
Wetenschap
Natuurkundigen ontwikkelen een lineaire responstheorie voor open systemen met uitzonderlijke punten

De lineaire responstheorie die in dit werk is ontwikkeld, geeft een volledige karakterisering van de relatie tussen uitgangs- en ingangssignalen (aangegeven door respectievelijk groene en gele pijlen) in termen van de eigenmodes en de canonieke toestanden van de onderliggende niet-Hermitiaanse Hamiltoniaan. Krediet:Ramy El-Ganainy
Lineaire analyse speelt een centrale rol in wetenschap en techniek. Zelfs als het om niet-lineaire systemen gaat, is het begrijpen van de lineaire respons vaak cruciaal om inzicht te krijgen in de onderliggende complexe dynamiek. De laatste jaren is er veel belangstelling voor het bestuderen van open systemen die energie uitwisselen met een omringend reservoir. In het bijzonder is aangetoond dat open systemen waarvan de spectra niet-Hermitische singulariteiten vertonen die uitzonderlijke punten worden genoemd, een groot aantal intrigerende effecten kunnen vertonen met mogelijke toepassingen bij het bouwen van nieuwe lasers en sensoren.
Op een uitzonderlijk moment worden twee of modi precies identiek. Laten we, om dit beter te begrijpen, eens kijken hoe drums geluid produceren. Het membraan van de trommel is langs de omtrek vastgezet, maar kan in het midden vrij trillen.
Als gevolg hiervan kan het membraan op verschillende manieren bewegen, die elk een modus worden genoemd en een andere geluidsfrequentie vertonen. Wanneer twee verschillende modi met dezelfde frequentie oscilleren, worden ze gedegenereerd genoemd. Uitzonderlijke punten zijn zeer eigenaardige degeneraties in die zin dat niet alleen de frequenties van de modi identiek zijn, maar ook de oscillaties zelf. Deze punten kunnen alleen bestaan in open, niet-Hermitiaanse systemen zonder analoog in gesloten, Hermitische systemen.
In de afgelopen jaren heeft ad-hocanalyse van de verstrooiingscoëfficiënten van niet-Hermitische systemen met uitzonderlijke punten een raadselachtig resultaat opgeleverd. Soms kan hun frequentierespons (de relatie tussen een uitgangs- en ingangssignaal na interactie met het systeem als een functie van de frequentie van het ingangssignaal) Lorentzian of super Lorentzian zijn (d.w.z. een Lorentzian verheven tot een geheel getal). Daarentegen is de respons van een standaard lineaire, geïsoleerde oscillator (met uitzondering van situaties waarin Fano-lijnvormen kunnen optreden) altijd Lorentziaans.
Een internationaal team van natuurkundigen onder leiding van Ramy El-Ganainy, universitair hoofddocent aan de Michigan Technological University, pakte dit probleem aan in hun recente Nature Communications artikel getiteld "Lineaire responstheorie van open systemen met uitzonderlijke punten." Het team presenteert een systematische analyse van de lineaire respons van niet-Hermitische systemen met uitzonderlijke punten. Belangrijk is dat ze een gesloten expressie afleiden voor de resolvent-operator die de respons van het systeem kwantificeert in termen van de rechter en linker eigenvectoren en Jordan canonieke vectoren geassocieerd met de onderliggende Hamiltoniaan.
"In tegenstelling tot eerdere uitbreidingen van de resolvent-operator in termen van de Hamiltoniaan zelf, biedt het hier ontwikkelde formalisme directe toegang tot de lineaire respons van het systeem en laat het precies zien wanneer en hoe Lorentz- en super-Lorentz-responsen ontstaan", zegt prof. El. -Ganany.
"Het bleek dat de aard van de respons wordt bepaald door de excitatie- (input) en collectie (output) kanalen", zegt Amin Hashemi, de eerste auteur van het manuscript. De gepresenteerde theorie beschrijft dit gedrag in detail en is generiek genoeg om van toepassing te zijn op alle niet-Hermitiaanse systemen met een willekeurig aantal uitzonderlijke punten van elke orde, waardoor het instrumentaal is voor het bestuderen van niet-Hermitische systemen met grote vrijheidsgraden.
The paper also includes authors from Penn State, the Humboldt University in Berlin, and the University of Central Florida. + Verder verkennen
Researchers design new emulator that reveals the intricacies of light behavior in complex evolving systems
 Nieuwe supramoleculaire copolymeren aangedreven door zelfsortering van moleculen
Nieuwe supramoleculaire copolymeren aangedreven door zelfsortering van moleculen De microstructuur van paracetamol
De microstructuur van paracetamol Onderzoekers ontwikkelen duurzame methode om vanilline te winnen uit houtverwerkingsafval
Onderzoekers ontwikkelen duurzame methode om vanilline te winnen uit houtverwerkingsafval Slimme materialen die in ultrageluid worden gebruikt, gedragen zich vergelijkbaar met water, chemici melden
Slimme materialen die in ultrageluid worden gebruikt, gedragen zich vergelijkbaar met water, chemici melden Een nieuwe methode voor het modelleren van interacties tussen geneesmiddelen en doelwitten herstelt een nadelige vooringenomenheid van technieken uit het verleden
Een nieuwe methode voor het modelleren van interacties tussen geneesmiddelen en doelwitten herstelt een nadelige vooringenomenheid van technieken uit het verleden
Hoofdlijnen
- Een nieuwe strategie die door Helicobacter pylori wordt gebruikt om mitochondriën aan te pakken
- Colombia,
- Zijn domme mensen gelukkiger?
- Een dodelijke ziekte heeft zeven Australische kikkersoorten met uitsterven gedreven. Maar deze bedreigde kikker vecht terug
- Onderzoekers rapporteren tandeloze bevindingen in odontode-dragende meervalstudie
- Is er eerder enige vorm van exploratie op Mercurius gedaan
- Radiometrische datering: definitie, hoe werkt het, gebruik & voorbeelden
- 's Werelds eerste geval van vogelgriep bij bruinvis:Zweden
- Internationale concurrentiebenchmarks metagenomics-software
- Machtige morphing materialen nemen complexe vormen aan

- Snel bewegende excitonen voor het eerst waargenomen in metaal, waardoor potentieel wordt ontsloten om digitale communicatie te versnellen
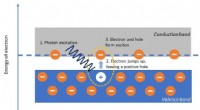
- Mysterieus Majorana-quasideeltje is nu dichter bij controle voor kwantumcomputers
- Hoe Pi te gebruiken om gebied en omtrek te berekenen
- Een atoom kietelen om het gedrag van materialen te onderzoeken

 Behoefte aan snelheid maakt genoombewerking efficiënt, zo niet beter
Behoefte aan snelheid maakt genoombewerking efficiënt, zo niet beter Boeing, anderen beoordelen de impact van tarieven tussen de VS en China
Boeing, anderen beoordelen de impact van tarieven tussen de VS en China Vrouwen keren wereldwijd het tij in het klimaatbeleid en kunnen een nieuw tijdperk inluiden voor Australië
Vrouwen keren wereldwijd het tij in het klimaatbeleid en kunnen een nieuw tijdperk inluiden voor Australië Met het HUMANS-project, een bericht dat ruimte voor iedereen is
Met het HUMANS-project, een bericht dat ruimte voor iedereen is Wat is een positieve controle in de microbiologie?
Wat is een positieve controle in de microbiologie?  Defecten kunnen wetenschappers helpen de exotische fysica van topologie te begrijpen
Defecten kunnen wetenschappers helpen de exotische fysica van topologie te begrijpen Amerikaanse toezichthouder heeft Twitter ondervraagd over valse accounts
Amerikaanse toezichthouder heeft Twitter ondervraagd over valse accounts General Motors zegt dat de staking heeft geleid tot een verlies van $ 194 miljoen in het vierde kwartaal
General Motors zegt dat de staking heeft geleid tot een verlies van $ 194 miljoen in het vierde kwartaal
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

