Wetenschap
Nieuw fysiek beeld leidt tot een nauwkeurige eindige-grootte schaling van (3+1)-dimensionaal O(n) kritisch systeem
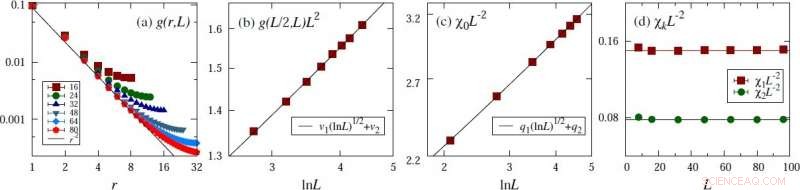
Bewijs voor de veronderstelde schaalvorm in het voorbeeld van het kritische 4D XY-model. (a) Tweepuntscorrelatiefunctie. (b) Tweepuntscorrelatie op de afstand van de helft van de lineaire systeemgrootte. (c) Magnetische gevoeligheid. (d) Magnetische fluctuaties bij niet-nul Fourier-modi. Krediet:©Science China Press
Sinds de oprichting van de renormalisatiegroepentheorie, het is bekend dat systemen van kritische fenomenen typisch een bovenste kritische dimensie dc hebben (dc=4 voor het O(n)-model), zodanig dat in ruimtelijke dimensies op of hoger dan de dc, het thermodynamisch gedrag wordt bepaald door kritische exponenten die gemiddelde veldwaarden aannemen. In tegenstelling tot de eenvoud van het thermodynamisch gedrag, de theorie van finite-size scaling (FSS) voor de d> dc O(n)-model was verrassend subtiel en was tot voor kort onderwerp van voortdurend debat gebleven, wanneer een twee-lengte schaling ansatz voor de tweepuntscorrelatiefunctie werd vermoed, numeriek bevestigd, en deels ondersteund door analytische berekeningen.
Bij de bovenste kritische dimensionaliteit dc, multiplicatieve en additieve logaritmische correcties komen over het algemeen voor op het blote gemiddelde veldgedrag. De verduidelijking van logaritmische correcties in FSS wordt 'notoir moeilijk, ' vanwege het gebrek aan analytische inzichten buiten het fenomenologische niveau en de limiet van systeemgroottes die beschikbaar zijn in numerieke simulaties. De precieze logaritmische FSS-vorm bij d=dc is al lang een probleem gebleven.
Onlangs, Jian-Ping Lv, Wanwan Xu, en Yanan Sun van de Anhui Normal University, Kun Chen uit Rutgers, de Staatsuniversiteit van New Jersey, en Youjin Deng van de Universiteit voor Wetenschap en Technologie van China en de Universiteit van Minjiang gingen in op de logaritmische FSS van de O(n)-symmetrie in de bovenste kritische dimensionaliteit. Inzichten lenen uit hogere dimensies, ze hebben een expliciete schaalvorm vastgesteld voor de vrije energiedichtheid, die tegelijkertijd bestaat uit een schaalterm voor het Gaussiaanse vaste punt en een andere term met multiplicatieve logaritmische correcties. Vooral, ze vermoedden dat de kritische tweepuntscorrelatie van eindige grootte een gedrag met twee lengtes vertoont, die wordt beheerst door een Gaussiaans vast punt op kortere afstand, en betreedt een plateau op grotere afstand waarvan de hoogte afneemt met de systeemgrootte in een machtswet gecorrigeerd door een logaritmische exponent.
Op deze basis, de FSS van verschillende macroscopische grootheden werden voorspeld. Vervolgens voerden ze uitgebreide Monte Carlo-simulaties uit voor het n-vectormodel met n=1, 2, 3, en verkregen solide bewijs ter ondersteuning van de veronderstelde schaalvormen van de FSS van de gevoeligheid, de magnetische fluctuaties bij niet-nul Fourier-modi, het bindmiddel cumulant, evenals de tweepuntscorrelatie op de afstand van de helft van de lineaire systeemgrootte. Dit is een belangrijke stap in de richting van een complete oplossing van de logaritmische FSS bij d=dc voor systemen met een hogere kritische dimensionaliteit.
De studie is niet alleen van theoretisch belang in modelsystemen, maar ook van praktisch belang voor een groot aantal experimentele systemen. Opgemerkt wordt dat als gevolg van technologische ontwikkelingen, de experimentele realisatie van het O(n)-model is nu beschikbaar in verschillende fysieke systemen, waaronder kwantummagnetische materialen, Josephson junction arrays, en ultrakoude atoomsystemen. Volgens de kwantum-naar-klassieke mapping, de driedimensionale quantum O(n)-systemen bevinden zich op de bovenste kritische dimensionaliteit.
Hoofdlijnen
- Iraakse dierenliefhebbers gaan online om zwerfdieren in Bagdad te redden
- mRNA: definitie, functie en structuur
- 10 planten verloren in de geschiedenis
- Lijst van de toepassingen van elektroforese
- Onderzoekers onthullen het mechanisme waarmee cellulaire kernen hun positie in spiercellen bereiken
- Hier is hoe planten- en dierencellen verschillen
- Sumatraanse neushoorns zijn nooit hersteld van verliezen tijdens het Pleistoceen, genoom bewijs toont
- Depolarisatie en herpolarisatie van het celmembraan
- Mensen gebruiken niet zoveel denkkracht als we graag denken
 Hoe de veranderende katoensector in India tot ellende heeft geleid, ziekten, mislukking
Hoe de veranderende katoensector in India tot ellende heeft geleid, ziekten, mislukking Zwitserland in epicentrum van cryptocurrency-revolutie
Zwitserland in epicentrum van cryptocurrency-revolutie Onderzoek onderzoekt voor het eerst de voordelen en kosten van nieuwe waterhergebruiksystemen
Onderzoek onderzoekt voor het eerst de voordelen en kosten van nieuwe waterhergebruiksystemen Uber koopt Midden-Oosten rivaal Careem:rapport
Uber koopt Midden-Oosten rivaal Careem:rapport Overstromingsgevoelige populaties met bijna 25% gestegen sinds 2000:studie
Overstromingsgevoelige populaties met bijna 25% gestegen sinds 2000:studie Nucleus-specifieke röntgenkleuring voor 3D virtuele histologie
Nucleus-specifieke röntgenkleuring voor 3D virtuele histologie Kunstmatige intelligentie-bot getraind om sterrenstelsels te herkennen
Kunstmatige intelligentie-bot getraind om sterrenstelsels te herkennen New Horizons-team repeteert voor nieuwjaarsvlucht
New Horizons-team repeteert voor nieuwjaarsvlucht
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com