
Wetenschap
Toegang krijgen tot scrambling in kwantumsystemen met behulp van matrixproductoperators
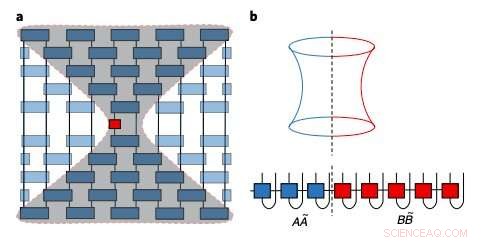
Schets van de opkomende lichtkegel en verstrengelingsstructuur van lokale Heisenberg-operators in tensornetwerkvormen. Krediet:Xu &Swingle.
In de kwantumfysica, scrambling is de verspreiding van kwantuminformatie over een complex kwantumsysteem, zoals chaotische quantum veellichamensystemen. Dit proces kan ervoor zorgen dat kwantuminformatie moeilijk of onmogelijk toegankelijk is, vooral bij het gebruik van eenvoudige en conventionele natuurkundige methoden.
Scrambling kan worden gemeten met behulp van out-of-time-ordered correlatoren (OTOC's), dat zijn maatregelen van kwantumchaos die verband houden met de groei van Heisenberg-operators. Onderzoekers van de Universiteit van Maryland hebben onlangs een nieuwe methode geïntroduceerd om OTOC's van lokale operators in 1-D-systemen te berekenen. Deze methode, gepresenteerd in een paper gepubliceerd in Natuurfysica , zou uiteindelijk kunnen worden gebruikt om scrambling in complexe kwantumsystemen te bestuderen.
"Het fundamentele probleem dat we probeerden te begrijpen, is hoe chaos zich verspreidt in de ruimte in kwantumsystemen, "Brian Swing, een van de onderzoekers die het onderzoek heeft uitgevoerd, vertelde Phys.org. "Denk aan het gedachte-experiment met het vlindereffect - we wilden weten:als een vlinder met zijn vleugels klappert, hoe snel verspreidt die verstoring zich in de ruimte? We wilden dit specifiek begrijpen in de context van kwantumsystemen die uit veel deeltjes bestaan."
Eerdere studies die onderzochten hoe chaos zich verspreidt in de ruimte binnen kwantumsystemen, hebben verschillende interessante observaties verzameld, het schilderen van een interessant maar vrij complex landschap van mogelijk gedrag. Veel van deze onderzoeken, echter, waren gebaseerd op speciale veronderstellingen en dit maakt het moeilijker om te bepalen in hoeverre hun conclusies kunnen worden gegeneraliseerd naar andere systemen.
In hun studie hebben Swingle en zijn collega Shenglong Xu wilden onderzoeken welk gedrag dat in eerdere onderzoeken is onthuld, generiek is voor alle kwantumsystemen. Ze hoopten ook te begrijpen hoe men kan denken over het landschap van mogelijkheden die zich voordoen in verschillende speciale systemen.
"Om grip te krijgen op wat het generieke gedrag was, we hadden een methode nodig om OTOC's in generieke systemen te berekenen, "Zei Swingle. "Zo'n methode zou een generieke eigenschap van OTOC's in lokale systemen moeten gebruiken."
Het idee van de onderzoekers was om de lichtkegeleigenschap van kwantumsystemen te gebruiken, wat inhoudt dat buiten de uitdijende kegel van invloed die voortkomt uit de vleugelflap van de metaforische vlinder, het systeem wordt nauwelijks verstoord. Met andere woorden, buiten de 'vlinderkegel' blijft het effect van de vlinder klein.
In de kwantummechanica, acties worden weergegeven als operators en de kleinheid van een bepaald effect vertaalt zich in de eenvoud van de operator. Door gebruik te maken van deze eenvoud, Swingle en Xu waren in staat om de operator op een rekenkundig bruikbare manier weer te geven (d.w.z. als 'matrixproductoperator'), om de berekeningen uit te voeren die nodig zijn om toegang te krijgen tot scrambling.
"Er zijn twee belangrijke resultaten in onze studie, ' zei Swingle. 'Eerst, we bedachten een theoretisch kader om verschillende mogelijke gedragingen van de OTOC te classificeren. Dit raamwerk was algemeen genoeg om alle eerder bekende voorbeelden op te nemen. Tweede, we hebben een methode voor algemene doeleinden geformuleerd om OTOC's te berekenen, een methode die verder kan gaan dan eerdere berekeningen."
Swingle en Xu hebben hun methode voor het berekenen van OTOC's van lokale operators al gebruikt om verschillende generieke systemen te bestuderen. interessant, ze ontdekten dat verschillende van deze systemen in hun theoretisch kader passen. In een vervolgonderzoek dat in Fysieke beoordeling X , de onderzoekers gebruikten hun methode ook om bewijs te verzamelen dat OTOC's in generieke chaotische systemen universeel gedrag vertonen.
"We hebben dit werk opgevolgd door onze technologie toe te passen op verschillende systemen die worden bestudeerd in tafelblad-experimenten over de hele wereld, "Swingle zei. "We zijn nu ook de aanpak aan het veralgemenen om nieuwe soorten effecten op te nemen, inclusief het bestuderen van systemen bij lage temperatuur waar de snelheid van verspreiding van chaos de neiging heeft te vertragen."
© 2019 Wetenschap X Netwerk
 Wetenschappers onderzoeken elektronische eigenschappen van vloeibare elektrolyten voor energietechnologieën
Wetenschappers onderzoeken elektronische eigenschappen van vloeibare elektrolyten voor energietechnologieën Mosselen inspireren nieuwe technologie die kan helpen water te zuiveren en olievlekken op te ruimen
Mosselen inspireren nieuwe technologie die kan helpen water te zuiveren en olievlekken op te ruimen "How to Make Liquid CO2
"How to Make Liquid CO2 Van kegelslakkengif tot pijnverlichting
Van kegelslakkengif tot pijnverlichting Het periodiek systeem 180 graden draaien voor een nieuw perspectief
Het periodiek systeem 180 graden draaien voor een nieuw perspectief
 Onderzoek onthult waarom mensen bepaalde campings kiezen
Onderzoek onthult waarom mensen bepaalde campings kiezen Om de catastrofale branden van de toekomst te bestrijden, we moeten verder kijken dan voorgeschreven verbranding
Om de catastrofale branden van de toekomst te bestrijden, we moeten verder kijken dan voorgeschreven verbranding Hoe kunnen we de fotodegradatie van plastic versnellen?
Hoe kunnen we de fotodegradatie van plastic versnellen?  2 bevingen in de buurt van Grieks eiland binnen 7 minuten
2 bevingen in de buurt van Grieks eiland binnen 7 minuten Soorten dieren in het gematigde bos en struikgewas
Soorten dieren in het gematigde bos en struikgewas
Hoofdlijnen
- Native Plants & Animals of France
- Het verschil tussen Anaphase, Interphase, Metaphase en Prophase
- Verrassing in de kangoeroe-stamboom - een buitenstaander is een naast familielid, ten slotte
- Kun je je familie aanzien voor bedriegers?
- Dakgoten wemelen van onopvallend leven
- Groep:Orang-oetanwezen een teken van vernietiging van hun leefgebied
- Geen toverstaf nodig:wetenschappers stellen een manier voor om elke cel in een ander celtype te veranderen
- Hoe genenbanken werken
- Hoge verwachtingen van Australische poging om pandawelpen te fokken
- Nieuw geometrisch model verbetert voorspellingen van vloeistofstroom in gesteente
- Niet te groot, niet te klein:analogie van Goudlokje gevonden in doolhofnavigatie

- The Deserts Renewable Resources

- Licht uitwisbaar geheugen veelbelovend voor systeem-op-paneel displays

- Voordelen en nadelen van thermische energie

 Radiofysici bestuderen de eigenschappen van composieten voor 5G-apparaten
Radiofysici bestuderen de eigenschappen van composieten voor 5G-apparaten NASA-gegevens helpen bij het opbouwen van veerkracht naarmate rampen heviger worden
NASA-gegevens helpen bij het opbouwen van veerkracht naarmate rampen heviger worden Boston Dynamics geeft Atlas een parkour-repertoire
Boston Dynamics geeft Atlas een parkour-repertoire Hubble ontdekt mysterieuze schijf van zwart gat
Hubble ontdekt mysterieuze schijf van zwart gat De kinderen die het meeste uit buitenschoolse activiteiten halen, missen iets:Hoe de toegang te verbeteren?
De kinderen die het meeste uit buitenschoolse activiteiten halen, missen iets:Hoe de toegang te verbeteren? Onderzoekers zetten methaan onder milde omstandigheden met hoge efficiëntie om in mierenzuur
Onderzoekers zetten methaan onder milde omstandigheden met hoge efficiëntie om in mierenzuur Maak je handen vuil voor de gezondheid
Maak je handen vuil voor de gezondheid Heroverweging van de basiswetenschap van grafeensynthese toont de weg naar productie op industriële schaal
Heroverweging van de basiswetenschap van grafeensynthese toont de weg naar productie op industriële schaal
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

