
Wetenschap
Holografie en kriticiteit in matchgate-tensornetwerken
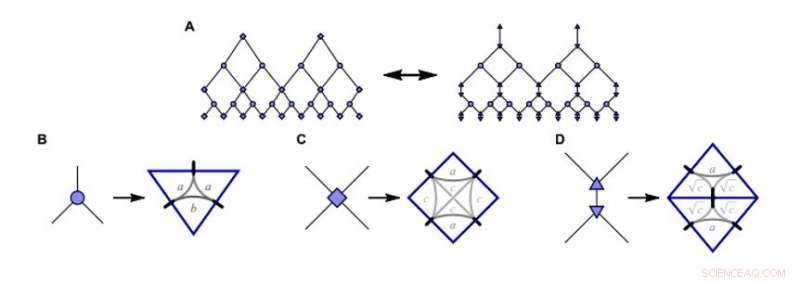
Het construeren van het matchgate MERA (multiscale entanglement renormalization ansatz simulation; mMERA) speelgoedmodel. A:Het standaard MERA-tensornetwerk (links) in de numerieke matchgate-instelling van het onderzoek is gelijk aan B-D:isometrieën, ontklitters, en driehoekige ontklitters (van links naar rechts), uitgedrukt als matchgate-tensoren. De vrije parameters a, B, c fixeer de componenten van de genererende matrices. Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aaw0092
Tensornetwerken spelen een centrale rol in de kwantumfysica omdat ze een efficiënte benadering kunnen bieden voor specifieke klassen van kwantumtoestanden. De bijbehorende grafische taal kan ook gemakkelijk beschrijven en picturaal redeneren over kwantumcircuits, kanalen, protocollen en open systemen. In een recente studie, A. Jahn en een onderzoeksteam in de afdelingen complexe kwantumsystemen, materialen en energie en wiskunde en informatica in Duitsland introduceerden een veelzijdig en efficiënt raamwerk om tensornetwerken te bestuderen door eerdere tools uit te breiden. De onderzoekers gebruikten bulk tiling (geometrische computertechniek) in hun werk om zeer nauwkeurige kritische gegevens te verkrijgen en legden een verband tussen holografische kwantumfoutcorrigerende codes en tensornetwerken. Ze verwachten dat het werk verder onderzoek van tensornetwerkmodellen zal stimuleren om bulk-grenscorrespondenties vast te leggen. De resultaten zijn nu gepubliceerd op wetenschappelijke vooruitgang .
De AdS/CFT-correspondentie, wat staat voor anti-de Sitter/conforme veldtheorie correspondentie, is een van de grootste onderzoeksgebieden in de snaartheorie, en is een voorbeeld in de context van bulk-grensdualiteiten waarin een holografische dualiteit bestaat tussen zwaartekracht in een bulkruimte en een kritisch kwantumveld op zijn grens. Deze correspondentie die twee zeer verschillende theorieën met elkaar in verband brengt, werd oorspronkelijk geformuleerd door natuurkundige Juan M. Maldacena in 1997, en wordt beschouwd als een significant belangrijk resultaat in de snaartheorie in de afgelopen 20 jaar.
Een belangrijk kenmerk van deze dualiteiten is de relatie tussen bulkgeometrie en grensverstrengelingsentropieën, die natuurkundigen eerder hadden verlicht met behulp van de Ryu-Takayanagi-formule. Aangezien het belangrijk is om verstrengeling te begrijpen in de context van AdS/CFT, onderzoekers realiseerden zich de noodzaak van tensornetwerken als een ideaal raamwerk om holografische speelgoedmodellen te construeren, zoals de multiscale verstrengeling renormalisatie ansatz simulatie (MERA). Natuurkundigen hadden eerder het besef onderzocht dat kwantumfoutcorrectie kan worden vergemakkelijkt door een holografische dualiteit, die verder verband hielden met ideeën uit de kwantuminformatietheorie. Hoewel onderzoekers met succes verschillende tensornetwerkmodellen hebben geconstrueerd om een verscheidenheid aan aspecten op AdS/CFT te reproduceren, ze hadden nog steeds geen algemeen begrip van de kenmerken en limieten van tensornetwerkholografie. Specifieke obstakels voor het proces zijn de potentieel grote parameterruimten van tensornetwerken en de aanzienlijke rekenkosten die ermee gemoeid zijn.
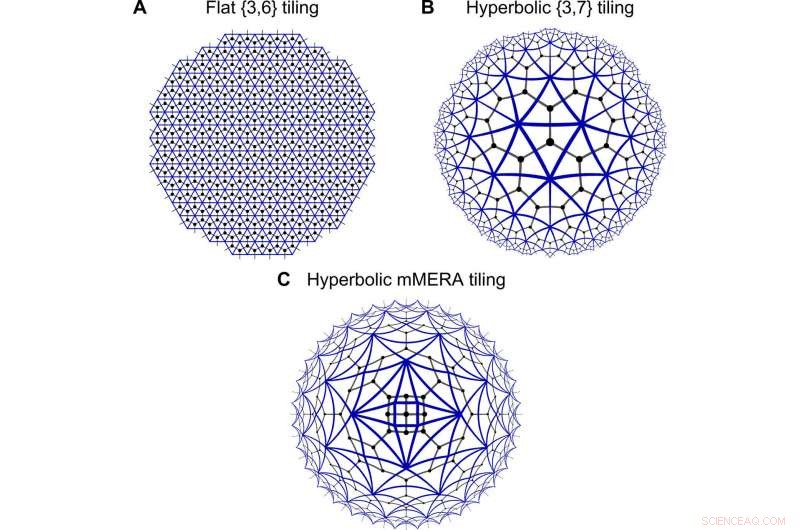
Geometrieën van tensornetwerken. Discretisaties van platte (A) en hyperbolische ruimte (B en C) met een driehoekige betegeling (blauwe randen), waarin een tensornetwerk is ingebed (zwart rooster). In het matchgate-formalisme, voegranden tussen driehoeken komen overeen met een integratie over een paar Grassmann-getallen, analoog aan de contractie van het tensornetwerk over indices. Terwijl (A) en (B) regelmatige tegels tonen, (C) presenteert een niet-reguliere MERA-achtige tegels, die de wetenschappers de matchgate MERA (mMERA) noemden. Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aaw0092
In het huidige werk, Jahn et al. overwon de bestaande uitdagingen door zeer efficiënte contractietechnieken toe te passen die zijn ontwikkeld door matchgate-tensoren. Dankzij de veelzijdige technieken kon het onderzoeksteam het samenspel van geometrie en correlaties in Gaussiaanse fermionische tensornetwerken uitgebreid bestuderen door speelgoedmodellen voor kwantumfoutcorrectie op te nemen. Ze omvatten ook eerdere benaderingen van het tensornetwerk, zoals het "MERA"-model in het huidige werk, om verbanden tussen hen te benadrukken. Het team beperkte de studie tot tensornetwerken die niet-unitair en reëel zijn, die lijkt op een Euclidische evolutie van de bulk naar de grens. Jahn et al. bood nieuwe benaderingen in de context van renormalisatie van het tensornetwerk, om het vermogen van tensornetwerken te onderbouwen om bulk-grenscorrespondenties te beschrijven die verder gaan dan bekende modellen. Het huidige werk is voorlopig en biedt een startpunt voor meer systematische studies over holografie in tensornetwerken.
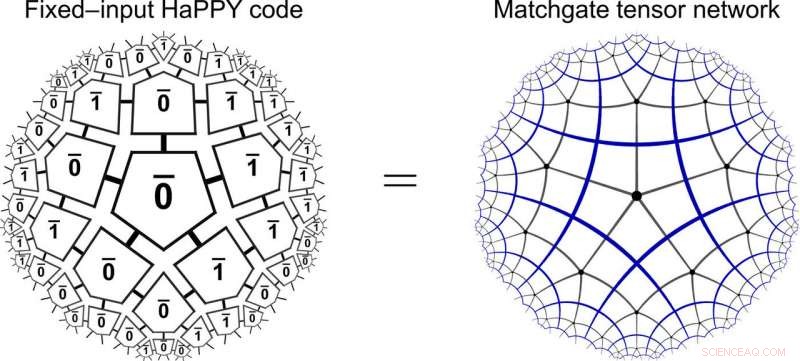
HaPPY/matchgate-equivalentie. De holografische vijfhoekcode van het HaPPY-model voor vaste computationele bulkinvoer (links) is gelijk aan een matchgate-tensornetwerk op een hyperbolische vijfhoekbetegeling (rechts). Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aaw0092
De wetenschappers pasten hun raamwerk eerst toe op de zeer symmetrische klasse van reguliere bulktegels om de elders voorgestelde holografische foutcorrectiecode (HaPPY-code) te implementeren. Daarna, ze onderzochten de veelzijdigheid van het raamwerk om het uit te breiden naar meer fysieke opstellingen. Ze gebruikten eerst het HaPPY-codespeelgoedmodel om de bulk / grensovereenstemming met bulkbetegeling van holografische vijfhoeken te begrijpen, waarbij elke vijfhoektegel één fouttolerante logische qubit codeerde. Kort, het onderzoeksteam merkte op dat het fixeren van de grootste vrijheidsgraden naar computationele basistoestanden aanleiding zou kunnen geven tot een matchgate-tensornetwerk. Ze toonden aan dat de computationele basistoestanden puur Gaussiaans zijn en concludeerden dat voor vaste computationele invoer in de bulk, de holografische pentagramcode zou een matchgate-tensor op de grens kunnen opleveren. Met behulp van een Schläfli-symbool {p, q} waarbij p =het aantal randen per polygoon en q =het aantal polygonen om elke hoek, ze specificeerden de hyperbolische geometrie van het HaPPY-model.
Nadat Jahn et al. toonden hun modelraamwerk om de holografische vijfhoekcode op te nemen die is opgebouwd uit vijf-qubit-stabilisatortoestanden voor vaste bulkinvoer. Ze toonden aan dat de grenstoestanden overeenkwamen met niet-lokale bulkparing met exotische deeltjes die bekend staan als Majorana-fermionen. Het werk opende dus een weg om de toestandseigenschappen van een holografisch model op grote schaal te bestuderen. De wetenschappers berekenden verder de tweepuntscorrelatoren en verstrengelingsentropieën van het systeem. Vervolgens toonden ze aan dat de kritische en gapped Gauss-grenstoestanden konden worden gerealiseerd buiten bekende modellen met behulp van verschillende bulktegels. In het huidige werk reproduceerden ze de gemiddelde schaaleigenschappen van het Ising CFT (conforme veldtheorie) speelgoedmodel; eenvoudigst mogelijke model in de theoretische fysica dat methoden van Euclidische kwantumveldentheorie en de studie van kritische verschijnselen mogelijk maakte.
-
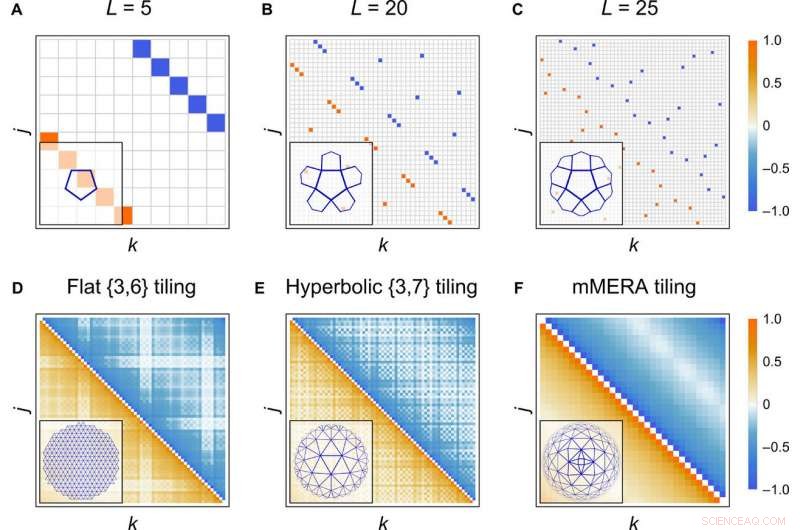
Grenstoestand correlaties. (A tot C) Majorana-covariantiematrix Γ met kleurgecodeerde vermeldingen voor een grenstoestand van een hyperbolische {5, 4} betegeling van de HaPPY-code met vaste 0¯-invoer op elke tegel. Grens bestaat uit 2L =10, 40, en 50 Majorana-sites, respectievelijk. (D tot F) Veldcorrelatiematrix 〈ψjψk − ψkψj〉/2 =(Γ2j, 2k−1 + Γ2j−1, 2k)/4 voor grenstoestanden van de {3, 6}, {3, 7}, en mMERA-tegels op kriticiteit met L =63, 69, en 64 grensplaatsen, respectievelijk. Matrixvermeldingen worden genormaliseerd naar dezelfde kleurenschaal. De tegels die overeenkomen met elke correlatiematrix in (A) tot (F) worden weergegeven in de linkerbenedenhoek. Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aaw0092
-
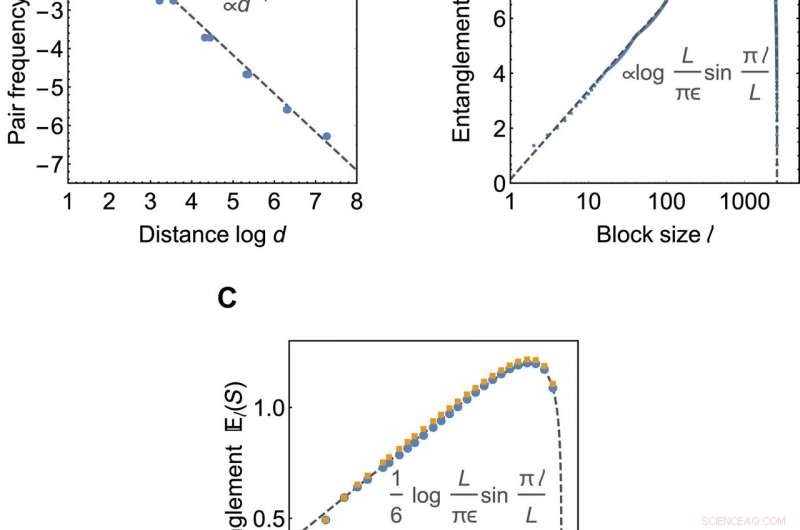
Kritische correlaties en verstrengelingsschaling. (A en B) Eigenschappen van de grenstoestand van de HaPPY-code op 2605 grenslocaties. (A) toont gemiddelde correlaties op grensafstand d, berekend als de relatieve frequentie n van Majorana-paren. Gestippelde grijze lijn toont een n(d)~1/d numerieke fit. (B) toont de schaling van de gemiddelde verstrengelingsentropie El (S) met subsysteemgrootte l. Gestippelde grijze lijn toont numerieke fit met behulp van (11). (C) El(S) voor regelmatige betegeling bij de kritische waarden a =0,580 voor een {3, 6} tegels (blauw) en bij a =0,609 voor de {3, 7} tegels (geel) met elk 348 grensplaatsen. De onderbroken grijze lijn toont de exacte c =1/2 CFT-oplossing. Krediet:wetenschappelijke vooruitgang, doi:10.1126/sciadv.aaw0092
Jahn et al. bouwde vervolgens een Euclidische matchgate-tensornetwerk op basis van de eerder ontwikkelde MERA-geometrie en noemde het de matchgate MERA (mMERA). Deze tegelinvariantie die ze uitdrukten als een triangulatie (meerdere maten om een construct vast te leggen), herstelde de Ising CFT met weinig rekenkosten. Het computationele optimalisatieproces in het onderzoek duurde slechts een paar minuten op een desktopcomputer voor een netwerk met honderden tensoren.
Op deze manier, A. Jahn en collega's introduceerden een efficiënt voorlopig raamwerk om tensornetwerken te bestuderen en stelden voor verdere studies binnen de Gauss-setting voor om zich te concentreren op positief gekromde bulks, hogere dimensionale modellen en willekeurige tensoren. Aanvullende studies buiten Gaussianity zouden interagerende fermionische tensornetwerken kunnen onderzoeken door expansie van zwakke koppelingen of onder lokaal beperkte interacties. Beide voorgestelde mogelijke uitbreidingen van het raamwerk dat in de studie wordt gepresenteerd, vereisen alleen computationele schaalpolynoom tot de systeemgrootte om onbetaalbare rekeninspanningen van algemene methoden om tensorcontractie te extraheren te voorkomen.
© 2019 Wetenschap X Netwerk
 Wetenschappers ontcijferen het multi-domein, volledige structuur van de humane smoothened receptor
Wetenschappers ontcijferen het multi-domein, volledige structuur van de humane smoothened receptor Onderzoekers beoordelen de vooruitgang in 3D-printen van legeringen met hoge entropie
Onderzoekers beoordelen de vooruitgang in 3D-printen van legeringen met hoge entropie Oxide sinteren door luchtdrukregeling
Oxide sinteren door luchtdrukregeling Ontwerpen van hiërarchische nanoporeuze membranen voor zeer efficiënte adsorptie- en opslagtoepassingen
Ontwerpen van hiërarchische nanoporeuze membranen voor zeer efficiënte adsorptie- en opslagtoepassingen Kooldioxide transformeren
Kooldioxide transformeren
 Wat zit er in uw drinkwater?
Wat zit er in uw drinkwater? Steden aangespoord om samen te werken met wetenschappers op het gebied van klimaatverandering
Steden aangespoord om samen te werken met wetenschappers op het gebied van klimaatverandering Overstromingen in Paraguay dwingen duizenden huizen te evacueren
Overstromingen in Paraguay dwingen duizenden huizen te evacueren Afbeelding:Proba-V-afbeeldingen Salar de Uyuni
Afbeelding:Proba-V-afbeeldingen Salar de Uyuni Satellietgebaseerde schattingen van verminderde ontbossing in beschermde gebieden nodig
Satellietgebaseerde schattingen van verminderde ontbossing in beschermde gebieden nodig
Hoofdlijnen
- Verschil tussen plant- en diercelafdeling
- Voorkeuren voor het eten van insecten voorspellen na ontbossing
- Nieuwe high-throughput sequencing-technologieën onthullen een wereld van op elkaar inwerkende micro-organismen
- Eerste Amerikaanse vrouw bevalt van getransplanteerde baarmoeder
- Waarom dromen we?
- Hoe Royal Jelly wordt geoogst?
- Wat zijn de verschillen tussen een plant en een dierlijke cel onder een microscoop?
- Hoe wetenschappers de gezondheid van walvissen in de gaten houden door drones te gebruiken om hun slag op te vangen
- Ons begrip vergroten van de impact van verbindingen geproduceerd door bepaalde visparasieten
- Wetenschappers vestigen record voor interactie tussen licht en materie

- Onderzoekers sturen de stroom van elektrische stroom met ronddraaiend licht

- Non-line-of-sight beeldvorming met picoseconde temporele resolutie

- Ancient Egyptian Astrology Facts

- Kernfysici springen in quantum computing met eerste simulaties van atoomkern

 Gletsjers kunnen het verhaal van de coronaviruspandemie vastleggen
Gletsjers kunnen het verhaal van de coronaviruspandemie vastleggen Anatomie van een kosmische zeemeeuw
Anatomie van een kosmische zeemeeuw Onderzoekers ontwikkelen nieuwe toolkit voor actie op het gebied van sociale rechtvaardigheid
Onderzoekers ontwikkelen nieuwe toolkit voor actie op het gebied van sociale rechtvaardigheid Hoe de massa van een voorwerp zijn beweging beïnvloedt
Hoe de massa van een voorwerp zijn beweging beïnvloedt Sporen van de vroege magma-oceaan van de aarde geïdentificeerd in Groenlandse rotsen
Sporen van de vroege magma-oceaan van de aarde geïdentificeerd in Groenlandse rotsen 40 procent van Oahu, De stranden van Hawaï zouden tegen het midden van de eeuw verloren kunnen gaan
40 procent van Oahu, De stranden van Hawaï zouden tegen het midden van de eeuw verloren kunnen gaan In het licht van COVID-19, studie kijkt naar afwegingen tussen economische waarde en volksgezondheid
In het licht van COVID-19, studie kijkt naar afwegingen tussen economische waarde en volksgezondheid Onderzoeker stelt twee Jack the Ripper-brieven vast die door één persoon zijn geschreven
Onderzoeker stelt twee Jack the Ripper-brieven vast die door één persoon zijn geschreven
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

