Wetenschap
Parrondos-paradox met een driezijdige munt
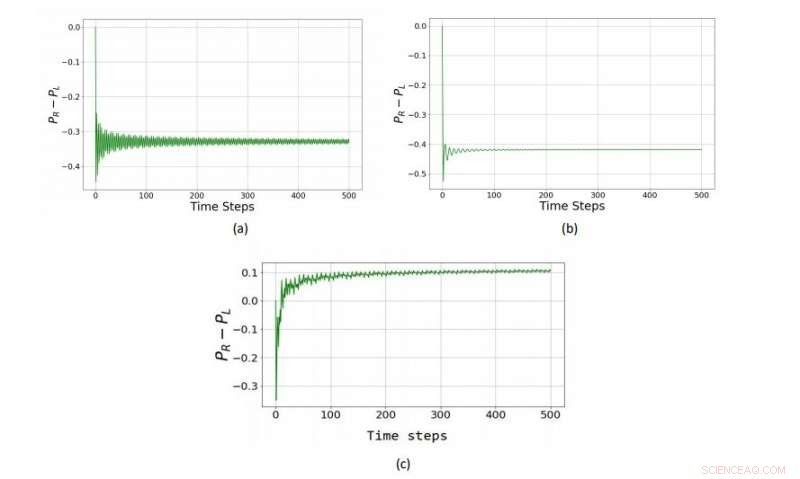
In een kwantumversie van een Parrondo-spel gespeeld met een munt met drie staten (een qutrit), de twee verliezende strategieën (a) en (b) worden gecombineerd tot een winnende strategie (c). Krediet:Rajendran et al. © 2018 EPL
Natuurkundigen hebben aangetoond dat Parrondo's paradox - een schijnbare paradox waarin twee verliezende strategieën samen een winnende strategie vormen - kan ontstaan als een muntspel met een enkele munt in het kwantumrijk, maar alleen als de munt drie toestanden heeft (kop, staarten, en een kant) in plaats van de conventionele twee.
In het algemeen, Parrondo's paradox, ook wel een Parrondo's spel genoemd, werkt alleen wanneer de twee verliezende strategieën op de een of andere manier van elkaar afhankelijk zijn en op zo'n manier worden gecombineerd dat de omstandigheden die ertoe leiden dat ze verliezen, veranderen. Sinds het in 1996 werd ontdekt door natuurkundige Juan Parrondo, Parrondo's paradox heeft toepassingen gevonden in de techniek, financiën, en evolutionaire biologie, onder andere gebieden.
Een van de eenvoudigste manieren om een Parrondo-spel te implementeren, wordt beschreven in dit Wikipedia-artikel. Stel dat je $ 100 hebt, en je kunt ervoor kiezen om elke combinatie van twee spellen te spelen. In het eerste spel, je verliest $1 elke keer dat je speelt. In het tweede spel, je wint $ 3 als je een even aantal dollars over hebt, en je verliest $ 5 als je een oneven aantal dollars over hebt. Als je alleen het eerste spel of alleen het tweede spel speelt, uiteindelijk verlies je al je geld, dus elk spel op zichzelf spelen is een verliezende strategie. Echter, als je wisselt tussen de twee spellen, beginnend met het tweede spel, dan win je $2 voor elke twee games die je speelt, zodat de twee verliezende strategieën kunnen worden gecombineerd tot een winnende strategie.
In de nieuwe studie natuurkundigen Jishnu Rajendran en Colin Benjamin van het National Institute of Science Education and Research, HBNI, in India, een spel van Parrondo hebben gedemonstreerd met een munt met drie staten, die ze vertegenwoordigen met een qutrit, een kwantumsysteem met drie toestanden.
"Parrondo's games zijn gezien in een klassieke context, "Benjamin vertelde" Phys.org . "Ons doel in dit werk was om te laten zien hoe het te implementeren in een kwantumcontext, in het bijzonder in een kwantumwandeling. Helaas, de kwantumversie van dit spel, wanneer geïmplementeerd met een enkele munt (qubit) in een kwantumwandeling, faalde in de asymptotische limieten. Wat we in dit werk laten zien, is dat een qutrit dit Parrondo-spel kan implementeren in een kwantumwandeling."
In de kwantumwandeling, een speler begint bij de oorsprong en beweegt naar rechts (positieve richting) of naar links (negatieve richting) volgens het resultaat van een toss. Als hoofden, de speler beweegt naar rechts; als staarten, links; en als het resultaat "kant, " dan interpreteert de speler dat als een "wachttoestand" en blijft op dezelfde plaats. Omdat de qutrit een kwantumsysteem is, het kan ook in een superpositie van deze toestanden zijn, in dat geval gaat de speler naar een overeenkomstige positie, ergens tussen een volledige stap links of rechts in. Aan het einde van het spel, als de kans dat de speler rechts van de oorsprong wordt gevonden groter is dan de kans dat hij links van de oorsprong wordt gevonden, de speler wint. Anders, zij verliezen.
Met behulp van enkele van de standaardmethoden in de deeltjesfysica om de concepten van het opgooien van munten en spelregels met een superpositie van toestanden te definiëren, de natuurkundigen demonstreerden verschillende voorbeelden van games die leiden tot verliezen wanneer ze individueel worden gespeeld, maar wanneer gecombineerd in een afwisselende reeks resulteren in een winnende uitkomst. Ze demonstreerden ook voorbeelden van het omgekeerde. Bijvoorbeeld, twee games die resulteren in een overwinning en een gelijkspel wanneer ze individueel worden gespeeld, kunnen resulteren in een verliezende uitkomst wanneer ze worden gecombineerd.
De natuurkundigen toonden ook aan dat, hoewel het niet mogelijk is om een Parrondo-spel te implementeren met een enkele dubbelzijdige munt (qubit), het is mogelijk om een Parrondo's spel uit te voeren met twee dubbelzijdige munten (twee qubits). De extra staten bieden in wezen extra flexibiliteit om strategieën te combineren die de voorwaarden van verlies kunnen overwinnen.
Gezien de brede toepassingen van de klassieke Parrondo-spellen, de natuurkundigen verwachten dat de kwantumversie kan leiden tot nieuw inzicht in het ontwerpen van kwantumalgoritmen.
"Parrondo's spel is een recept om te bewijzen dat je niet altijd hoeft te zoeken naar een winnende strategie (of algoritme) in een spel, "Zei Benjamin. "Klassiek, er zijn veel toepassingen van Parrondo's spellen, variërend van het uitleggen van fysiologische processen in de cel tot het vergroten van ons begrip van Brownse motoren en zelfs in gediversifieerde portefeuillebeleggingen. klassiek, Het is aangetoond dat Parrondo's paradox werkt met behulp van klassieke willekeurige wandelingen.
"Het implementeren van een Parrondo-spel in een kwantumwandeling zou implicaties hebben voor het bedenken van betere of snellere kwantumalgoritmen. Een algoritme dat gebruikmaakt van kwantumprincipes zoals superpositie en/of verstrengeling is een kwantumalgoritme. Een algoritme, als het kan worden geïmplementeerd op een kwantumwandeling, zou lucratiever zijn dan een methode die alleen kan worden uitgevoerd op een klassieke random walk. Omdat kwantumwandelingen zich kwadratisch sneller verspreiden dan klassieke willekeurige wandelingen, een algoritme dat op een kwantumwandeling is geïmplementeerd, zal veel minder tijd in beslag nemen dan een algoritme op een klassieke willekeurige wandeling. Verder, de succesvolle implementatie van Parrondo's spel op een kwantumwandeling biedt een algoritmische verklaring voor kwantumratels [systemen die slechts in één richting bewegen]."
© 2018 Fys.org
 Gestructureerde materialen op meerdere schalen voor elektrokatalyse en foto-elektrokatalyse
Gestructureerde materialen op meerdere schalen voor elektrokatalyse en foto-elektrokatalyse Density to Molarity Conversion
Density to Molarity Conversion Onderzoekers klokken DNA's hersteltijd na chemotherapie
Onderzoekers klokken DNA's hersteltijd na chemotherapie Tweetalig molecuul verbindt twee basiscodes voor het leven
Tweetalig molecuul verbindt twee basiscodes voor het leven Onderzoekers werken samen met kleine bedrijven in NM om nieuwe beademingsmaterialen te testen
Onderzoekers werken samen met kleine bedrijven in NM om nieuwe beademingsmaterialen te testen
 Onderzoekers voeren eerste wereldwijde beoordeling uit van de uitstoot van broeikasgassen in de levenscyclus van kunststoffen
Onderzoekers voeren eerste wereldwijde beoordeling uit van de uitstoot van broeikasgassen in de levenscyclus van kunststoffen Koralen uit de schemerzone:wie eet wat op een diep Rode Zee-rif
Koralen uit de schemerzone:wie eet wat op een diep Rode Zee-rif Landelijke Amerikanen strijden tegen vervuiling door fabrieksboerderijen vinden grip in de rechtbank
Landelijke Amerikanen strijden tegen vervuiling door fabrieksboerderijen vinden grip in de rechtbank China wordt geconfronteerd met aanzienlijk warmere zomers en winters in 2050
China wordt geconfronteerd met aanzienlijk warmere zomers en winters in 2050 Het risico op bosbranden is dit jaar weer hoog - dit is wat reizigers moeten weten
Het risico op bosbranden is dit jaar weer hoog - dit is wat reizigers moeten weten
Hoofdlijnen
- Diffusie: wat is het? & Hoe gebeurt het?
- Farmacie Onderzoek Onderwerpen
- Hoe hebben wetenschappers ontdekt dat genen zijn gemaakt van DNA?
- Interacties tussen eenvoudige moleculaire mechanismen leiden tot complexe infectiedynamiek
- Eiwit beperkt de opname van sap door bladluizen
- Mottenvrouwtjes gebruiken geurnabijheid om partners aan te trekken
- Een orchidee die nooit bloeit
- Is er een zaak tegen geluk?
- Welke bijdrage heeft Avery geleverd aan de ontdekking van DNA?
 Ga naar de kassa? Niet op je mobiel, zeggen onderzoekers
Ga naar de kassa? Niet op je mobiel, zeggen onderzoekers Alt-Labour invullen waar vakbonden niet kunnen
Alt-Labour invullen waar vakbonden niet kunnen De grootste partiële zuurstofdruk in het circulatiesysteem
De grootste partiële zuurstofdruk in het circulatiesysteem NASA vindt een sterkere tropische cycloon Uesi in de buurt van Nieuw-Caledonië
NASA vindt een sterkere tropische cycloon Uesi in de buurt van Nieuw-Caledonië Bosbranden in Californië hebben NorCals Air de ergste ter wereld gemaakt
Bosbranden in Californië hebben NorCals Air de ergste ter wereld gemaakt  Ng /Ml naar IU
Ng /Ml naar IU Natuurkundigen creëren een platform om ultrasterke foton-naar-magnon-koppeling te bereiken
Natuurkundigen creëren een platform om ultrasterke foton-naar-magnon-koppeling te bereiken Gemodificeerd enzym kan de productie van ethanol van de tweede generatie verhogen
Gemodificeerd enzym kan de productie van ethanol van de tweede generatie verhogen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Swedish | German | Dutch | Danish | Norway | Portuguese |

-
Wetenschap © https://nl.scienceaq.com