Wetenschap
Grasshopper-probleem geeft inzicht in kwantumtheorie
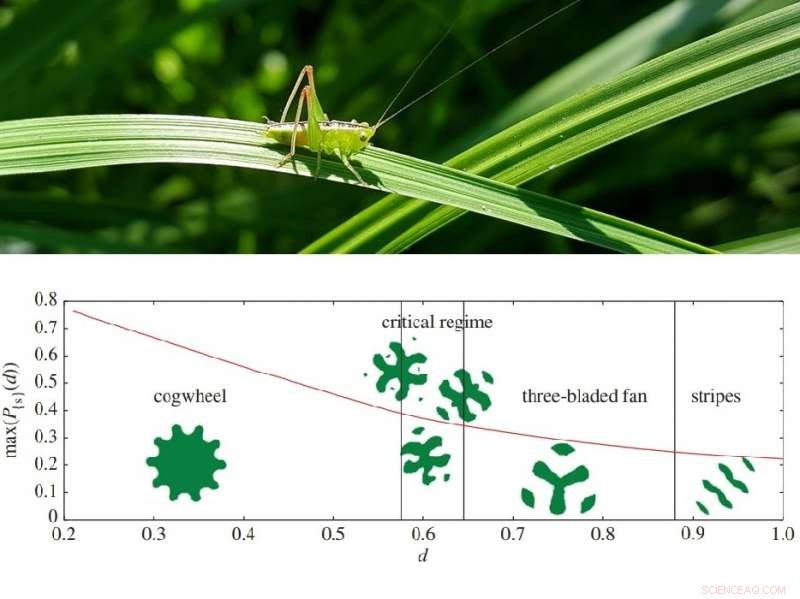
Enkele van de optimale gazonvormen, die afhangen van de afstand die de sprinkhaan springt. Voorbij het kritische regime, de beste configuraties zijn losgekoppeld. Schema tegoed:Goulko et al. De Koninklijke Maatschappij. Krediet:Pixabay.
(Phys.org)—Zoals veel wiskundige puzzels, het sprinkhaanprobleem is eenvoudig te formuleren maar moeilijk op te lossen:een sprinkhaan landt op een willekeurig punt op een grasveld van gebied 1, springt dan een keer, een vaste afstand, in een willekeurige richting. Welke vorm moet het gazon hebben om de kans te vergroten dat de sprinkhaan na het springen op het gazon blijft staan?
Een eerste indruk kan zijn dat het gazon de vorm van een cirkel moet hebben, tenminste als de afstand die de sprinkhaan springt klein is. Echter, Olga Goulko en Adrian Kent, de twee natuurkundigen die het sprinkhanenprobleem introduceerden in een nieuw artikel, hebben wiskundig bewezen dat een schijfvormig gazon voor geen enkele afstand optimaal is.
In plaats daarvan, ze ontdekten door middel van numerieke simulaties dat de optimale gazonvorm verschillende complexe vormen aanneemt voor verschillende springafstanden, zoals een tandradvorm voor afstanden kleiner dan 1/π 1/2 (de straal van een cirkel van gebied 1, of ongeveer 0,56), terwijl voor grotere afstanden, het optimale gazon bestaat uit losgekoppelde stukken. Vaak, maar niet altijd, deze optimale vormen bezitten een soort symmetrie.
Gemotiveerd door natuurkunde
Behalve dat het een interessant meetkundig probleem is, het sprinkhanenprobleem hangt ook nauw samen met onderzoek in de kwantumfysica en kan verschillende technologische toepassingen hebben. Vooral, het sprinkhanenprobleem is verbonden met de Bell-ongelijkheden, die laten zien dat, in tegenstelling tot klassieke natuurkundige modellen, de kwantumtheorie gehoorzaamt niet aan het lokale realisme. Een goed voorbeeld van de schending van lokaal realisme is te zien in kwantumverstrengeling, waarin twee verre verstrengelde systemen correlaties vertonen die niet kunnen worden verklaard door een model dat gehoorzaamt aan het lokale realisme.
Deze verbinding met de Bell-ongelijkheid is, in feite, wat oorspronkelijk Goulko en Kent motiveerde om het sprinkhanenprobleem voor te stellen. Een open probleem in de natuurkunde met betrekking tot de ongelijkheden van Bell is om de optimale grenzen te bepalen die door de kwantumtheorie worden geschonden wanneer kwantumcorrelaties worden gemeten op een bol onder hoeken tussen 0 en 90 graden. Het blijkt dat dit probleem van het bepalen van de optimale grenzen equivalent is aan het probleem van het bepalen van de gazonvorm van het sprinkhaanprobleem wanneer het gazon bolvormig is in plaats van vlak. In de sferische versie van het sprinkhanenprobleem, de afstand die de sprinkhaan over vlakke grond springt wordt vervangen door de hoek waaronder hij over de bol springt.
In hun krant die is gepubliceerd in een recent nummer van de Proceedings van de Royal Society A , Goulko en Kent hebben alleen de vlakke versie van het sprinkhanenprobleem geanalyseerd, hoewel ze verwachten dat het niet al te moeilijk moet zijn om dezelfde numerieke technieken toe te passen op het sferische geval. Vervolgens, wanneer rekening wordt gehouden met enkele aanvullende beperkingen, het is misschien mogelijk om eindelijk het probleem van de optimale grenzen van de Bell-ongelijkheden op te lossen.
"We zijn van plan om verder te werken aan de sferische versies van het sprinkhanenprobleem die relevant zijn voor de ongelijkheden van Bell, en verwachten dat onze methoden daar zouden moeten werken, "Kent vertelde" Phys.org .
Nieuwe grens
Zoals de natuurkundigen uitleggen, een van de verrassende dingen van het sprinkhanenprobleem is dat er nog nooit zoiets is voorgesteld. Hoewel het basisidee zo eenvoudig is dat het probleem zou kunnen zijn gesteld door de oude Griekse wiskundige Euclides, die de basis legde voor de moderne geometrie, de onderzoekers zijn niet op de hoogte van een eerdere versie van het probleem, hetzij in de oudheid of in de moderne tijd.
"Het is fijn om eraan herinnerd te worden dat zelfs in een veld zo oud als de geometrie, men kan nog steeds eenvoudige nieuwe vragen vinden die verrassende antwoorden hebben en nieuwe onderzoekslijnen openen, ' zei Kent.
Als een gloednieuw probleem, er zijn een eindeloos aantal toekomstige onderzoeksrichtingen te nemen. Bijvoorbeeld, de natuurkundigen stellen voor om de sprinkhaan meerdere sprongen te laten maken, of vereisen dat de sprinkhaan op alle punten van zijn pad op het gazon loopt en blijft (een variatie die ze het "mierenprobleem" noemen). Andere mogelijke variaties zijn onder meer generaliseren naar hogere dimensies, het analyseren van andere gazonoppervlakken dan bollen en vlakken, overwegende een variatie van het probleem met twee verschillende soorten gazonzaad die elkaar in dezelfde regio kunnen overlappen (wat vooral relevant is voor Bell-ongelijkheid), en het plaatsen van extra beperkingen op de mogelijke oplossingen.
Natuurlijk, zulke vragen gaan niet echt over sprinkhanen en gazons, omdat de onderliggende structuur een manier biedt om verschillende situaties uit de echte wereld te modelleren. Een voorbeeld waar de onderzoekers op wijzen zijn nucleaire kettingreacties. In een kettingreactie, een hoogenergetisch deeltje botst op een willekeurige atoomkern, waardoor het splijting ondergaat, dat een ander hoogenergetisch deeltje produceert dat een bepaalde afstand aflegt om een andere willekeurige kern te raken, en het proces herhaalt zich. Door deze situatie te modelleren met het sprinkhanenprobleem, het optimale gazonoppervlak komt overeen met de maximale initiële reactiesnelheid, die het aantal kernen dat deelneemt aan de kettingreactie maximaliseert.
Een andere mogelijke toepassing van het sprinkhanenprobleem ligt in het modelleren van kwantumcommunicatieprotocollen, die de onderzoekers uitleggen, kan worden gezien als een sprinkhaanmodel waarin een partij moet kiezen welk algoritme (gazonvorm) moet worden gebruikt om met een tweede partij te communiceren.
En tenslotte, de onderzoekers suggereren dat het interessant kan zijn om te kijken naar de oorsprong van de gazonvormen zelf, omdat sommige gazonpatronen lijken op patronen die herhaaldelijk in de natuur voorkomen, zoals in bloemen, schelpen, en dierenstrepen. In overeenstemming met de theorie van morfogenese voorgesteld door Alan Turing, deze patronen kunnen om chemische redenen als optimale oplossingen ontstaan, wat kan helpen bij het verklaren van de diverse en complexe vormen van de gazons die voorkomen in het sprinkhanenprobleem.
© 2017 Fys.org
 Behoud van visbiomassa de sleutel tot het behoud van de biodiversiteit van rifvissen
Behoud van visbiomassa de sleutel tot het behoud van de biodiversiteit van rifvissen Californië staat in brand. Van over de Stille Oceaan, Australiërs kijken toe en riemen vast
Californië staat in brand. Van over de Stille Oceaan, Australiërs kijken toe en riemen vast Onderzoekers modelleren regionale effecten van specifieke antropogene activiteiten, hun invloed op extreem brandweerrisico
Onderzoekers modelleren regionale effecten van specifieke antropogene activiteiten, hun invloed op extreem brandweerrisico Leven onder extreme omstandigheden bij warmwaterbronnen in de oceaan
Leven onder extreme omstandigheden bij warmwaterbronnen in de oceaan GOES-16-satelliet stuurt eerste beelden van de aarde
GOES-16-satelliet stuurt eerste beelden van de aarde
Hoofdlijnen
- Ambtenaren:walvissen, na een dodelijk jaar, zou kunnen uitsterven
- Sint-jakobsschelpen hebben 200 ogen, die functioneren als een telescoop:studie
- UVB-straling beïnvloedt het gedrag van stekelbaarzen
- Gegevensmodellering is de sleutel tot duurzaam visserijbeheer
- Vier hoofdgroepen organische verbindingen waaruit levende organismen bestaan
- Waarom kunnen we de voetstappen van anderen horen,
- Spanje meldt geval van gekkekoeienziekte
- Ongedierteresistentie tegen biotech-gewassen stijgt
- Indonesische smokkelaars stopten exotische vogels in pijpen:politie
 Digitale kwantumsimulators kunnen verbazingwekkend robuust zijn
Digitale kwantumsimulators kunnen verbazingwekkend robuust zijn De aarde is een minder vluchtige versie van de zon, studie vondsten
De aarde is een minder vluchtige versie van de zon, studie vondsten In het oude Arabië, sommige tools zijn gemaakt om te pronken met vaardigheden
In het oude Arabië, sommige tools zijn gemaakt om te pronken met vaardigheden Devos:mobiele app komt voor federale aanvraag voor studentenhulp
Devos:mobiele app komt voor federale aanvraag voor studentenhulp Zou een CO2-belasting helpen om efficiënter energiegebruik te innoveren?
Zou een CO2-belasting helpen om efficiënter energiegebruik te innoveren? Welke rol spelen superzware zwarte gaten wanneer sterrenstelsels samensmelten?
Welke rol spelen superzware zwarte gaten wanneer sterrenstelsels samensmelten? Hoe bedreigde pandas
Hoe bedreigde pandas Asteroïde Florence heeft twee manen
Asteroïde Florence heeft twee manen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com