
Wetenschap
Onderzoekers lossen een wiskundig probleem op dat wordt geïllustreerd door zeepfilms die flexibele lussen overspannen

Deze zeepfilm in een metalen staaf heeft kruispunten waar meerdere zeepfilms elkaar ontmoeten. In 2014, Prof. Jenny Harrison van UC Berkley breidde de oplossing voor het plateauprobleem uit om meer gecompliceerde zeepfilmvormen zoals deze te verklaren. Krediet:Okinawa Instituut voor Wetenschap en Technologie
Vaak gebruikt voor kinderplezier, zeepbellen zijn delicaat, lichtreflecterende films die meestal maar een paar seconden duren voordat ze barsten. Maar buiten hun waarde om te entertainen, zeepbellen zijn fysieke voorbeelden van het rijke wiskundige probleem van minimale oppervlakken; ze nemen de vorm aan van een zo klein mogelijk oppervlak, met een bepaald volume. Onderzoekers van de Okinawa Institute of Science and Technology Graduate University (OIST) hebben onlangs de oplossing uitgewerkt voor een wiskundig probleem - bekend als het Kirchhoff-Plateau-probleem - dat eenvoudig wordt geïllustreerd door zeepfilms die flexibele lussen overspannen.
"Onze oplossing van het Kirchhoff-Plateau-probleem levert prachtige wiskundige resultaten op die dicht bij wat er in de fysieke wereld gebeurt, " zegt dr. Giulio Giusteri, co-auteur van het artikel dat onlangs werd gepubliceerd in het Journal of Nonlinear Science. Dr. Giusteri werkte samen met professor Eliot Fried, die aan het hoofd staat van OIST's Mathematical Soft Matter Unit, en Dr. Luca Lussardi van de Università Cattolica del Sacro Cuore in Italië.
De vraag die het team beantwoordt is een variant van het "Plateauprobleem", een eeuwenoud wiskundig probleem, vernoemd naar de 19e-eeuwse Belgische natuurkundige, Joseph Plateau. Plateau veronderstelde dat wanneer je een stijf draadframe in een zeepoplossing dompelt, het oppervlak van de zeepfilm gevormd op het frame vertegenwoordigt een wiskundig minimaal mogelijk gebied, ongeacht de vorm van het frame.
De eerste bevredigende oplossing voor het plateauprobleem werd in de 20e eeuw gegeven, door de Amerikaanse wiskundige Jesse Douglas, waarvoor hij in 1936 de Fields Medal ontving. Meer recentelijk, in 2014, Professor Jenny Harrison van UC Berkeley breidde het werk van Douglas uit, het leveren van een bewijs dat geldig is onder algemene hypothesen, waaronder, bijvoorbeeld, situaties waarin knooppunten aanwezig zijn waar meerdere zeepfilms elkaar ontmoeten.
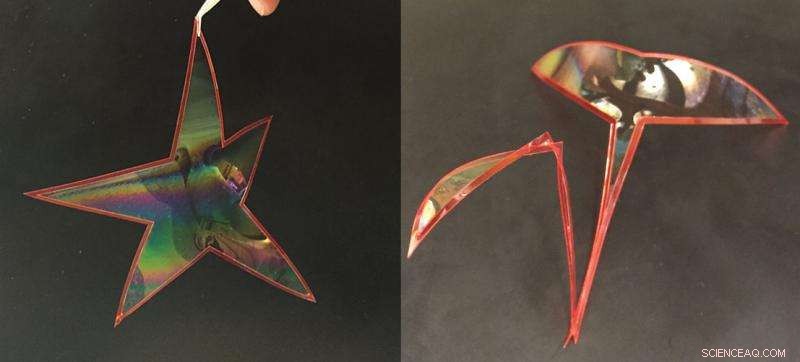
Zeepfilms in een flexibele lus oefenen een kracht uit op de lus, waardoor het van vorm verandert. Bijvoorbeeld, dezelfde lus kan een stervorm of een zwaanvorm vormen, afhankelijk van de oppervlaktespanning van de zeepfilm. Krediet:Okinawa Instituut voor Wetenschap en Technologie
In tegenstelling tot het Plateauprobleem waarbij een zeepfilm een vast frame overspant, het Kirchhoff-Plateau-probleem betreft de evenwichtsvormen van zeepfilms die flexibele lussen overspannen, gemaakt, bijvoorbeeld, van vislijn, dat kan worden beschreven met behulp van de staaftheorie van Kirchhoff - een model dat een krachtige benadering biedt voor het bestuderen van de statica en dynamica van dunne elastische staven. De complicatie is dat een flexibele lus van vorm kan veranderen als reactie op de kracht die wordt uitgeoefend door de zeepfilm. Als zodanig, een oplossing voor het probleem vereist niet alleen de vorm van de zeepfilm, maar ook de vorm van de begrenzingslus. In tegenstelling tot, de vorm van de begrenzing in het oorspronkelijke Plateau-probleem is bekend omdat deze is gemaakt van starre draad die gefixeerd blijft tegen de relatief zwakke krachten van de zeepfilm.
Een extra complicatie die samenhangt met het Kirchhoff-Plateau-probleem is dat, in tegenstelling tot het oorspronkelijke Plateau-probleem, waarbij de grens wordt verondersteld eendimensionaal te zijn, een Kirchhoff-staaf is een driedimensionaal object. Hoewel filamenten zoals vislijnen dun zijn, ze zijn orden van grootte dikker dan een zeepfilm in evenwicht, wat betekent dat het gebied van de zeepfilm kan veranderen afhankelijk van het punt waarop de film in contact komt met de lus.
De onderzoekers hebben al deze fysieke effecten met succes vertaald naar wiskundige termen. Zoals prof. Fried uitlegt:"Hoe sterk de concurrentie tussen de oppervlaktespanning van de zeepfilm en de elastische respons van de lus ook is, het systeem kan zich altijd aanpassen om een configuratie met de minste energie te bereiken."
De oplossing voor het Kirchhoff-Plateau-probleem draagt niet alleen bij aan het begrip van energie door wiskundige vormen te minimaliseren, maar kan ook worden toegepast op biologische systemen. Bijvoorbeeld, het zou ons kunnen helpen begrijpen hoe de vorm van een eiwit bepaalt hoe het interageert met en bindt aan een oppervlak.
Het team werkt nu aan computersimulaties die, op basis van dit wiskundige model, kan het gedrag van fysieke systemen voorspellen.
 Soap aan olie en water toevoegen
Soap aan olie en water toevoegen Onderzoekers gebruiken nieuwe tools van datawetenschap om afzonderlijke moleculen in actie vast te leggen
Onderzoekers gebruiken nieuwe tools van datawetenschap om afzonderlijke moleculen in actie vast te leggen Plastic dat de planeet redt? Nieuwe hars voor startups helpt de industrie groen te worden
Plastic dat de planeet redt? Nieuwe hars voor startups helpt de industrie groen te worden Welk deel van de nephron is verantwoordelijk voor de heropname van water?
Welk deel van de nephron is verantwoordelijk voor de heropname van water?  Uranium breekt weer met de regels
Uranium breekt weer met de regels
 Zwitserse wacht op grote hoogte voor verloren gletsjer
Zwitserse wacht op grote hoogte voor verloren gletsjer Nieuwe landbewegingskaart toont de menselijke impact op het Britse landschap
Nieuwe landbewegingskaart toont de menselijke impact op het Britse landschap Luchtvervuiling aanpakken:onderzoekers presenteren emissie-inventaris voor Nepal
Luchtvervuiling aanpakken:onderzoekers presenteren emissie-inventaris voor Nepal Hoe het stroomgebied van Hood River veerkrachtiger kan worden tegen klimaatverandering
Hoe het stroomgebied van Hood River veerkrachtiger kan worden tegen klimaatverandering Canada voldoet niet aan de doelstellingen voor duurzame ontwikkeling van de VN
Canada voldoet niet aan de doelstellingen voor duurzame ontwikkeling van de VN
Hoofdlijnen
- De centrale hoek vinden
- Waarom zijn de Neanderthalers uitgestorven?
- Wetenschappers zoeken naar overlevenden nadat de Thomas-brand een condorreservaat heeft verschroeid
- Over de zes koninkrijken
- Klimaatverandering maakt baardagamen mogelijk minder intelligent
- De methoden van inventarisatie in Microbes
- Zuid-Amerikaanse brulapen zijn mogelijk meer bedreigd dan eerder werd gedacht
- De Pomodoro-techniek:je kunt elke taak 25 minuten per keer aan
- Soorten spijsverteringsenzymen
- Magnetische stormen ontstaan dichter bij de aarde dan eerder werd gedacht, dreigende satellieten

- Optische singulariteiten kunnen worden gebruikt voor een breed scala aan toepassingen, van beeldvorming met superresolutie tot optische trapping
- Nieuwe lichttechniek zou kunnen resulteren in minder opdringerige, effectievere diagnose voor patiënten

- Grafeentrommel:een nieuw fonon-laserontwerp
- Wetenschappers ontwikkelen principes voor het maken van een akoestische diode

 De greep van India op steenkool losmaken zonder de miljoenen in de steek te laten die erop vertrouwen
De greep van India op steenkool losmaken zonder de miljoenen in de steek te laten die erop vertrouwen De aarde verduistert door klimaatverandering
De aarde verduistert door klimaatverandering Satellietwaarneming kan helpen bij overstroomde gebieden
Satellietwaarneming kan helpen bij overstroomde gebieden Op weg naar passief-mode-locked lasers met zichtbare golflengte in volledig vezelformaat
Op weg naar passief-mode-locked lasers met zichtbare golflengte in volledig vezelformaat EPA onthult strategie om giftige chemicaliën voor altijd te reguleren
EPA onthult strategie om giftige chemicaliën voor altijd te reguleren Digitale tweelingen van materialen maken
Digitale tweelingen van materialen maken Studie volgt ernstige verblekingsgebeurtenissen op een koraalrif in de Stille Oceaan in de afgelopen eeuw
Studie volgt ernstige verblekingsgebeurtenissen op een koraalrif in de Stille Oceaan in de afgelopen eeuw Hoe regelkleppen afstellen
Hoe regelkleppen afstellen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

