
Wetenschap
Een 50 jaar oude puzzel oplossen in signaalverwerking, deel twee
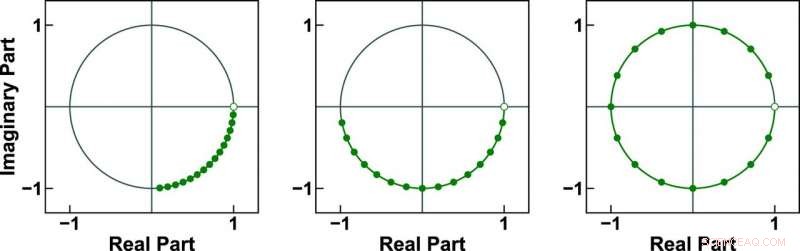
Hier zijn drie voorbeelden van 16-punts chirp-contouren op de eenheidscirkel. Het ICZT-algoritme dat is ontwikkeld door ingenieurs van Iowa State kan met alle drie werken, terwijl het eerder gebruikte algoritme alleen met de laatste contour kan werken. Krediet:Alexander Stojtchev.
Alexander Stoytchev van de Iowa State University zegt dat het een van de 'meest populaire en nuttige' algoritmen is die er zijn, hoewel de meesten van ons er nog nooit van hebben gehoord.
Maar, als je een mobiele telefoon hebt gebruikt, internetten of een medisch beeld nodig hadden, je hebt geprofiteerd van de snelle Fourier-transformatie (FFT).
De transformatie en zijn inverse (bekend als de IFFT) zijn sinds 1965 in gebruik. in uw mobiele telefoon wordt de FFT gebruikt om het ontvangen signaal van het basisstation (of zendmast) te analyseren. De IFFT lost het omgekeerde probleem op:het synthetiseert het signaal dat je telefoon naar het basisstation stuurt.
1969, onderzoekers ontwikkelden een bruikbaarder, gegeneraliseerde versie van de FFT bekend als de chirp z-transform (CZT). Maar niemand had een algemene versie van het IFFT bedacht. Het was een 50 jaar oude puzzel in signaalverwerking.
Dat is, tot afgelopen herfst toen twee ingenieurs van de staat Iowa - Stoytchev en Vladimir Sukhoy - in een onderzoekspaper aankondigden dat ze een oplossing in gesloten vorm hadden bedacht voor de inverse chirp z-transform (ICZT) en een snel algoritme om het te berekenen. (Het papier wekte veel interesse in de signaalverwerkingsgemeenschap, met meer dan 26, 000 toegangen sinds oktober.)
Nu melden Stoytchev - een universitair hoofddocent elektrotechniek en computertechniek die ook verbonden is aan het Virtual Reality Applications Center van de universiteit - en Sukhoy - een docent elektrotechniek en computertechniek - nieuwe onderzoeksresultaten over hun algoritme.
In een artikel dat zojuist online is gepubliceerd door Wetenschappelijke rapporten , een tijdschrift voor natuuronderzoek, de twee laten zien hoe hun algoritme functioneert "op de eenheidscirkel, " wat verwijst naar een speciaal geval van zijn parameters. (Hun vorige paper benadrukte alleen operaties "buiten de eenheidscirkel.")
Het artikel beschrijft hoe het algoritme kan werken met frequentiecomponenten die worden gegenereerd door meetpunten van de eenheidscirkel in het complexe vlak. Deze punten vormen een contour die bekend staat als de chirp-contour. In tegenstelling tot het IFFT, die alleen kan werken met bemonsteringspunten op gelijke afstand die de eenheidscirkel volledig bedekken, het ICZT-algoritme kan werken met contouren die slechts een fractie van de eenheidscirkel beslaan. Het kan ook werken met contouren die zich om de cirkel wikkelen en meerdere omwentelingen uitvoeren. Dit maakt het gebruik van bepaalde (niet-orthogonale) frequentiecomponenten mogelijk, die een van de belangrijkste beperkingen van het IFFT opheft en zou kunnen leiden tot een beter spectrumgebruik.
Het document identificeert de parameterwaarden waarvoor het algoritme numeriek nauwkeurig is en waarvoor niet, en beschrijft hoe de nauwkeurigheid ervan als functie van de parameters kan worden geschat. (Technische opmerking:het laat zien dat de singulariteiten van de ICZT van grootte n gerelateerd zijn aan de elementen van de Farey-reeks van orde n-1. Dit is een interessant verband omdat Farey-reeksen vaak voorkomen in de getaltheorie.)
Het blad laat zien dat, op de eenheidscirkel, het ICZT-algoritme bereikt een hoge nauwkeurigheid met alleen 64-bits drijvende-kommagetallen en vereist geen extra numerieke precisie, waardoor het gemakkelijker te implementeren is. Het rapporteert dat het algoritme goed kan combineren met het bestaande CZT-algoritme om back-to-back signaalanalyse en signaalsynthese uit te voeren. En het laat zien dat het algoritme snel is (het werkt in wat bekend staat als O(n log n) tijd).
"Dit algoritme is algemener dan het IFFT, maar behoudt dezelfde snelheid, ' zei Stoytchev.
Dat is goed nieuws voor de ingenieurs die werken aan het oplossen van allerlei uitdagingen op het gebied van signaalverwerking:
"Toepassingsdomeinen die hiervan kunnen profiteren, " schreven de ingenieurs van de staat Iowa in de krant, "omvat signaalverwerking, elektronica, medische beeldvorming, radar, sonar, draadloze communicatie, en anderen."
 Ontdekking opent nieuwe wegen voor het ontwerpen van medicijnen om resistente malaria te bestrijden
Ontdekking opent nieuwe wegen voor het ontwerpen van medicijnen om resistente malaria te bestrijden Hoe een destillatiesysteem te berekenen
Hoe een destillatiesysteem te berekenen Chaperones kunnen eiwitten in niet-evenwichtstoestanden vasthouden
Chaperones kunnen eiwitten in niet-evenwichtstoestanden vasthouden Een nieuw proces om metallurgische slakken te recyclen
Een nieuw proces om metallurgische slakken te recyclen Geen trial-and-error meer bij het kiezen van een elektrolyt voor metaal-luchtbatterijen
Geen trial-and-error meer bij het kiezen van een elektrolyt voor metaal-luchtbatterijen
 Wat zijn de voordelen van prokaryoten?
Wat zijn de voordelen van prokaryoten?  13 grote bedrijven dringen er bij Trump op aan om in Parijs-deal te blijven
13 grote bedrijven dringen er bij Trump op aan om in Parijs-deal te blijven Vergroening van het grijs:Overstromingen bestrijden met herstel versus riprap
Vergroening van het grijs:Overstromingen bestrijden met herstel versus riprap De definitie van abiotische en biotische factoren
De definitie van abiotische en biotische factoren Satelliet vindt windschering die tropische storm Nadine treft
Satelliet vindt windschering die tropische storm Nadine treft
Hoofdlijnen
- Zeehonden en onze kusten
- Wat is histonacetylatie?
- Animal Cell Shoe Box Project
- Trucs voor het onthouden van dierenfylum
- Onderzoekers ontdekken slecht begrepen bacteriële lijnen in de monden van dolfijnen
- Staan we allemaal af van een gemeenschappelijke vrouwelijke voorouder?
- Interacties tussen eenvoudige moleculaire mechanismen leiden tot complexe infectiedynamiek
- Bijenschadelijke pesticiden in 75 procent van de honing wereldwijd:studie
- Wanneer is een mutatie in een DNA-molecuul overgegaan op nakomelingen?
- MOOSE:een platform om complexe multifysica-simulaties te maken

- Lenige mini-cheetah-robot levert indrukwekkende backflip-prestaties

- Robots kunnen ons te slim af zijn op het virtuele slagveld, dus laten we ze niet de leiding geven over het echte werk

- Autonome drones die intelligent kunnen zien en vliegen

- Brussel overweegt autobelasting om files te verminderen

 Zou je het merken als je rekenmachine tegen je loog? Het onderzoek zegt waarschijnlijk niet
Zou je het merken als je rekenmachine tegen je loog? Het onderzoek zegt waarschijnlijk niet Hoe Mole Fractions te berekenen met behulp van massapercentage
Hoe Mole Fractions te berekenen met behulp van massapercentage  Wat seksisme in callcenters ons kan leren over seksisme in de samenleving
Wat seksisme in callcenters ons kan leren over seksisme in de samenleving Studie onderzoekt radio-eigenschappen van supernovarest G107.0+9.0
Studie onderzoekt radio-eigenschappen van supernovarest G107.0+9.0 Onderzoekers ontwikkelen synthetische nanodeeltjes HDL-cholesterol
Onderzoekers ontwikkelen synthetische nanodeeltjes HDL-cholesterol Methoden voor ontzilting
Methoden voor ontzilting Zuid-Italië:Aardbevingsgevaar door actieve plaatgrens
Zuid-Italië:Aardbevingsgevaar door actieve plaatgrens Zakelijke praktijken van modemerken ondermijnen vooruitgang bij het beëindigen van uitbuiting door kledingarbeiders
Zakelijke praktijken van modemerken ondermijnen vooruitgang bij het beëindigen van uitbuiting door kledingarbeiders
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

