
Wetenschap
64,3 gram opgeloste stof in 3,90 X 10Ë water verhoogt het kookpunt tot 100,680 °C?
$$\Delta T_b =K_b \maal m$$
waarbij ΔTb de verandering in kookpunt is, Kb de kookpuntverhogingsconstante van het oplosmiddel is, en m de molaliteit van de oplossing is.
Er wordt aangenomen dat ΔTb =100,680 °C - 100,000 °C =0,680 °C, en dat het oplosmiddel water is, dat een kookpuntverhogingsconstante heeft van Kb =0,512 °C/m.
Als we deze waarden in de vergelijking invullen, krijgen we:
$$0,680 °C =0,512 °C/m \maal m$$
Als we voor m oplossen, krijgen we:
$$m =1,33 mln$$
Dit betekent dat de oplossing 1,33 mol opgeloste stof per kilogram water bevat.
Om de molaire massa van de opgeloste stof te berekenen, kunnen we de volgende vergelijking gebruiken:
$$Molariteit =\frac{Moles\text{ van opgeloste stof}}{Liters\text{ van oplossing}}$$
We weten dat de oplossing 1,33 mol opgeloste stof bevat, en we kunnen de liters oplossing berekenen met behulp van de dichtheid van water (1 g/ml):
$$Liter\text{ oplossing} =\frac{3,90 \times 10^{2} g}{1 g/ml} =390 ml$$
Nu kunnen we de molmassaformule gebruiken:
$$Molariteit =\frac{1,33\text{ mol}}{0,390 \text{ L}}$$
Molariteit wordt:
$$Molariteit =3,41$$
Ten slotte gebruiken we de volgende vergelijking om de molaire massa van de opgeloste stof te berekenen:
$$Molar\text{ Massa} =\frac{Grams\text{ van opgeloste stof}}{Moles\text{ van opgeloste stof}}$$
Als we de waarden die we kennen vervangen, krijgen we:
$$Molar\text{ Massa} =\frac{64,3 g}{1,33 mol}$$
$$Molar\text{ Massa} =48,3\text{ g/mol}$$
Daarom is de molaire massa van de opgeloste stof 48,3 g/mol.
 Wat gebeurt er in een halfvaste stof als de concentratie opgeloste stof toeneemt?
Wat gebeurt er in een halfvaste stof als de concentratie opgeloste stof toeneemt?  Wat als HCl en Na2SO4 gemengd worden? Is dit een gevaarlijke reactie?
Wat als HCl en Na2SO4 gemengd worden? Is dit een gevaarlijke reactie?  Wat zijn de reacties van fotosynthese?
Wat zijn de reacties van fotosynthese?  Bacterieel eiwit kan helpen bij het vinden van materialen voor je volgende smartphone
Bacterieel eiwit kan helpen bij het vinden van materialen voor je volgende smartphone Wordt een verdunde zure oplossing alleen gemaakt van zwak zuur?
Wordt een verdunde zure oplossing alleen gemaakt van zwak zuur?
 Door te achterhalen hoe het leven op aarde is ontstaan, kan dit helpen verduidelijken waar het nog meer zou kunnen bestaan
Door te achterhalen hoe het leven op aarde is ontstaan, kan dit helpen verduidelijken waar het nog meer zou kunnen bestaan  Klimaateffecten zorgen voor een oost-west kloof in de productie van boszaad
Klimaateffecten zorgen voor een oost-west kloof in de productie van boszaad Europium wijst naar nieuwe verdachte in continentaal mysterie
Europium wijst naar nieuwe verdachte in continentaal mysterie Pastoralisten houden al duizenden jaren vee in barre klimaten. Wat kunnen ze ons vandaag de dag leren?
Pastoralisten houden al duizenden jaren vee in barre klimaten. Wat kunnen ze ons vandaag de dag leren?  De natuur moet centraal staan in de economie, zeggen onderzoekers
De natuur moet centraal staan in de economie, zeggen onderzoekers
Hoofdlijnen
- Behoud oproep aan zaagviskwekerij
- Is de vorm van een genoom net zo belangrijk als de inhoud ervan?
- Regenwormen kunnen zich voortplanten in Mars-bodemsimulant
- Het mysterie,
- Sardines nemen ons mee naar de bronnen van biodiversiteit in de Amazone-rivier
- Wat is de biologische levenscyclus van vleermuizen?
- Dieren zijn geëvolueerd om overexploitatie van hun hulpbronnen te voorkomen. Kunnen mensen hetzelfde doen?
- Onderzoekers brachten twee jaar door in diepe ondergrondse grotten om dit buitengewone fossiel aan het licht te brengen
- Als moeders de genen van de vader in plantenembryo's uitschakelen
- Lab-on-a-chip-test heeft potentieel om COVID-19-immuunrespons sneller te detecteren dan huidige antilichaamtesten

- Succes in het synthetiseren van biologisch afbreekbare plastic materialen met behulp van zonlicht en CO2
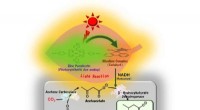
- Chemici ontwikkelen verschillende industrieel belangrijke synthetische processen

- Bio-geïnspireerd enzymmodel met een redox-schakelaar
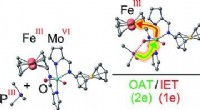
- Adsorberen of niet adsorberen? Dat is de vraag

 Hoe aardbevingen werken
Hoe aardbevingen werken  Hoe kunnen nieuwe cellen iemands gezichtsvermogen herstellen?
Hoe kunnen nieuwe cellen iemands gezichtsvermogen herstellen?  Wat zorgt ervoor dat een bewegend object in beweging blijft?
Wat zorgt ervoor dat een bewegend object in beweging blijft?  Niet alle dieren in het wild zijn hersteld in lockdowns, zo blijkt uit nieuw onderzoek
Niet alle dieren in het wild zijn hersteld in lockdowns, zo blijkt uit nieuw onderzoek Het aanpakken van geestelijke gezondheidsproblemen in kleine bedrijven kan een grote impuls geven aan de economie
Het aanpakken van geestelijke gezondheidsproblemen in kleine bedrijven kan een grote impuls geven aan de economie Wat als Homeostase faalt?
Wat als Homeostase faalt?  Bijdrage van bijna $ 5 miljard aan het BBP van de oceaan van Brits-Columbia, waarschijnlijk een onderschatting
Bijdrage van bijna $ 5 miljard aan het BBP van de oceaan van Brits-Columbia, waarschijnlijk een onderschatting Welke vergelijking wordt gebruikt om de hoeveelheid gebruikte elektrische energie te berekenen?
Welke vergelijking wordt gebruikt om de hoeveelheid gebruikte elektrische energie te berekenen?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

