
Wetenschap
Wordt de kracht toegenomen tot twee keer zoveel wanneer de afstand tussen twee sterren met de helft afneemt?
Newton's Law of Universal Gravitation
De zwaartekracht tussen twee objecten is recht evenredig met het product van hun massa en omgekeerd evenredig met het kwadraat van de afstand tussen hun centra. Wiskundig:
F =g * (m1 * m2) / r^2
Waar:
* F is de zwaartekracht
* G is de zwaartekrachtconstante
* M1 en M2 zijn de massa van de twee objecten
* r is de afstand tussen hun centra
De relatie tussen kracht en afstand
* omgekeerde vierkante wet: Let op de "r^2" in de noemer. Dit betekent als u halve halve halve halt De afstand (r/2), de kracht (f) wordt vermenigvuldigd met 4 (omdat (1/2)^2 =1/4).
In uw geval:
Als de afstand tussen twee sterren met de helft afneemt, zal de zwaartekracht tussen hen toeneemt met een factor vier, niet alleen het dubbele.
 Als je een atoom splitst, waarom ontploft het dan?
Als je een atoom splitst, waarom ontploft het dan?  Wat is de bijdrage van Arturo Alcaraz in de wetenschap?
Wat is de bijdrage van Arturo Alcaraz in de wetenschap?  Natuurkundigen ontdekken hoe ze de kristalstructuur van grafeen kunnen veranderen
Natuurkundigen ontdekken hoe ze de kristalstructuur van grafeen kunnen veranderen  Kunnen polaire moleculen en waarvoor opladers door het niet -polaire middengedeelte van fosfolipide dubbellaag sluipen?
Kunnen polaire moleculen en waarvoor opladers door het niet -polaire middengedeelte van fosfolipide dubbellaag sluipen?  Reageert chloor met waterstof om een ionische verbinding te vormen?
Reageert chloor met waterstof om een ionische verbinding te vormen?
 Een appel valt uit een boom. De zwaartekracht op de is 1 N. Als luchtweerstand 0,1 n welke netto appel?
Een appel valt uit een boom. De zwaartekracht op de is 1 N. Als luchtweerstand 0,1 n welke netto appel?  Welk effect heeft de wereldwijde luchtvaart op het milieu?
Welk effect heeft de wereldwijde luchtvaart op het milieu? Experts bespreken sterke en zwakke punten van de Green New Deal
Experts bespreken sterke en zwakke punten van de Green New Deal Het gebruik van systematische methoden om de sociale natuurlijke werelden te bestuderen en uit te leggen is de bedoeling?
Het gebruik van systematische methoden om de sociale natuurlijke werelden te bestuderen en uit te leggen is de bedoeling?  Captain Scotts Discovery-expeditie biedt 100 jaar later inzicht in klimaatverandering
Captain Scotts Discovery-expeditie biedt 100 jaar later inzicht in klimaatverandering
Hoofdlijnen
- Welk proces komt voor in een celmembraan?
- Waar in de cellen zijn instructies voor histogenese?
- Waarom wetenschappers Alfred Wegener geloven?
- Hoe DNA te maken met pijpreinigers & pony kralen
- Wat betekent substraten?
- Soorten bacteriën in levensmiddelen
- Wat is het onderdeel van fosfolipide?
- Wat hebben planten- en dierbacteriecellen gemeen?
- Welke streng mRNA zou worden geproduceerd uit het hieronder getoonde DNA?
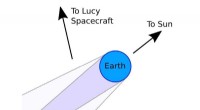
- NASA Lucy-missie observeert een totale maansverduistering
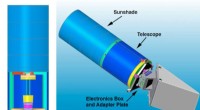
- NASA's ShadowCam wordt gelanceerd aan boord van Korea Pathfinder Lunar Orbiter
- Onderzoekers schatten de massa van de Melkweg op 890 miljard keer die van onze zon

- Bijna 80 exoplaneetkandidaten in recordtijd geïdentificeerd
- Op zoek naar de echte kleine rode beestjes in de Melkweg

 Hoe heet een getijdenretraite?
Hoe heet een getijdenretraite?  De zeeschildpad die weigerde te worden geslagen door de storm
De zeeschildpad die weigerde te worden geslagen door de storm Welk type kracht kan een verandering veroorzaken een snelheidsrichting van een objecten of beide?
Welk type kracht kan een verandering veroorzaken een snelheidsrichting van een objecten of beide?  Welke tak van de wetenschap behoort exobiologie?
Welke tak van de wetenschap behoort exobiologie?  Hoe kan een hellend vlak helpen om objecten te verplaatsen?
Hoe kan een hellend vlak helpen om objecten te verplaatsen?  Hoe kunt u een stroom in draad vergroten?
Hoe kunt u een stroom in draad vergroten?  Klimaatverandering:kan geo-engineering iedereen tevreden stellen?
Klimaatverandering:kan geo-engineering iedereen tevreden stellen?  Gedragsaanpassingen voor Sharks
Gedragsaanpassingen voor Sharks
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

