
Wetenschap
Model met gedraaid grafeen vertoont complex elektronisch gedrag
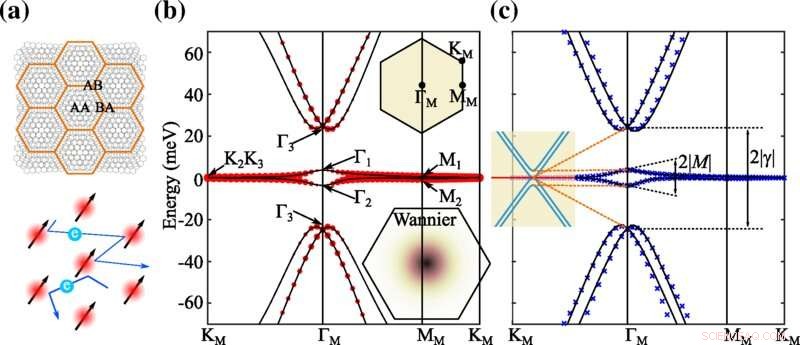
Topologisch zwaar fermionmodel. (a) Een schets van de moiré-eenheidscel van MATBG en zijn zware fermion-analoog, waar de lokale momenten en rondreizende elektronen worden gevormd door de effectieve f orbitalen bij de AA -stapelingsgebieden en topologische geleidingsbanden (c), respectievelijk. (b) De bandstructuur van het BM-model bij de magische hoek θ =1,05°, waarbij de moiré BZ en hoge symmetriemomenta worden geïllustreerd in het bovenste inzetpaneel. De overlappingen tussen de Bloch-staten en de proef-WF's worden weergegeven door de rode cirkels. Het dichtheidsprofiel van de geconstrueerde maximaal gelokaliseerde WF's ( f orbitalen) wordt weergegeven in het onderste inzetpaneel. (c) Banden gegeven door het topologische zware fermionmodel (zwarte lijnen) in vergelijking met de BM-banden (blauwe kruisjes). De c (blauw) en f banden (rood) in de ontkoppelde limiet, waarbij γ=v′⋆ =0 , worden weergegeven in de inzet. Oranje stippellijnen geven de evolutie van energieniveaus aan als f−c koppeling is ingeschakeld. Krediet:Fysieke beoordelingsbrieven (2022). DOI:10.1103/PhysRevLett.129.047601
Een paar onderzoekers, de een met Peking University, de ander met Princeton University, heeft ontdekt dat de parameters van de excitatiespectra van verdraaid grafeen rechtstreeks overeenkomen met kenmerken van het zware fermion-model. In hun paper gepubliceerd in het tijdschrift Physical Review Letters, Zhi-Da Song en B. Andrei Bernevig beschrijven het bouwen van een model om aspecten van het Bistritzer-MacDonald-model te laten zien en gebruikten het vervolgens om kenmerken van gedraaid dubbellaags grafeen aan te tonen. Aline Ramires van het Paul Scherrer Institute heeft een News &Views-artikel gepubliceerd in het tijdschrift Nature waarin het werk van Bernevig en Song wordt geschetst.
Grafeen is een platte, 2D-plaat van koolstof en een onderwerp van veel onderzoek. Een onderzoeksinspanning van vier jaar geleden omvatte het plaatsen van het ene vel grafeen op het andere en vervolgens het draaien van het bovenste vel. Na veel vallen en opstaan ontdekten die onderzoekers dat het draaien van het bovenste vel een bepaalde hoeveelheid (1,05 graden) leidde tot het creëren van een supergeleider. Dat bracht hen ertoe om naar de gedraaide hoeveelheid te verwijzen als een 'magische hoek'.
Sinds die tijd hebben andere onderzoekers de kenmerken van gedraaid dubbellaags grafeen bestudeerd, uitgelijnd op zijn magische hoek. In deze nieuwe poging bestudeerden de onderzoekers de excitatiespectra en ontdekten dat deze overeenkwamen met de parameters van het fermionmodel.
Eerder werk heeft aangetoond dat gedraaid dubbellaags grafeen met precies de juiste oriëntatie enkele unieke eigenschappen aanneemt - bijvoorbeeld één set elektronen beweegt rond, wat verantwoordelijk is voor de geleidbaarheid. Maar een andere set elektronen blijft gefixeerd. De twee tegenstrijdige eigenschappen van het materiaal stellen wetenschappers in staat een monster tussen een isolator en een supergeleider te duwen.
Om beter te begrijpen waarom dit gebeurt, hebben Song en Bernevig een model van het systeem gemaakt en dit vervolgens gebruikt om exacte berekeningen uit te voeren die het gedrag van het materiaal beschrijven. Ze ontdekten dat ze de structuur van gedraaid dubbellaags grafeen konden beschrijven in vergelijking met zware fermionmaterialen. Meer werk toonde aan dat de parameters van het materiaal direct overeenkwamen met de parameters van het zware fermion-model. Zware fermionmaterialen zijn die welke onderaan het periodiek systeem worden gevonden. + Verder verkennen
Speciaal georiënteerd gedraaid dubbellaags grafeen herbergt topologische elektronische toestanden
© 2022 Science X Network
 Science Projects on Laundry Detergents
Science Projects on Laundry Detergents Wetenschappers behalen nieuwe resultaten in de studie van anorganische pigmenten met apatietstructuur
Wetenschappers behalen nieuwe resultaten in de studie van anorganische pigmenten met apatietstructuur Nieuwe verbinding kan fotodynamische therapie voor kanker verbeteren
Nieuwe verbinding kan fotodynamische therapie voor kanker verbeteren Het effect van azijn op kippenbotten
Het effect van azijn op kippenbotten Nieuwe symmetriedoorbrekende methode opent weg voor bioactieve stoffen
Nieuwe symmetriedoorbrekende methode opent weg voor bioactieve stoffen
 Op het zuidelijk halfrond kan aan het einde van de eeuw tot 30% minder regen vallen
Op het zuidelijk halfrond kan aan het einde van de eeuw tot 30% minder regen vallen Een cloud-screeningschema voor de Chinese kooldioxide-observatiesatelliet (TanSat)
Een cloud-screeningschema voor de Chinese kooldioxide-observatiesatelliet (TanSat) Emeralds vinden in North Carolina
Emeralds vinden in North Carolina  De volgende black-out voorkomen
De volgende black-out voorkomen Hittegolven bedreigen de gezondheid van Australiërs en onze politici doen er niet genoeg aan
Hittegolven bedreigen de gezondheid van Australiërs en onze politici doen er niet genoeg aan
Hoofdlijnen
- Genetisch gemodificeerde paarse tomaten komen mogelijk naar een Amerikaanse supermarkt bij jou in de buurt
- Nieuwe cijfers tonen bevolkingsgroei nabij globes kwetsbare koraalriffen
- Factoren die van invloed zijn op celverdeling
- Studie vindt hoe de overlevingstijd van stamcellen kan worden verlengd
- Genexpressie in Prokaryotes
- Kan glucose door het celmembraan diffunderen door eenvoudige diffusie?
- Wat zijn de vijf klassen van immunoglobulines?
- Hoe hersenspoeling werkt
- Familiebanden geven dieren redenen om te helpen of kwaad te doen naarmate ze ouder worden
- Metalen manipuleren voor adaptieve camouflage

- Slim toetsenbord reinigt en voedt zichzelf - en kan zien wie je bent (update)

- Nanodeeltjes uit dranken met voedingssupplementen die waarschijnlijk in het milieu terechtkomen, zeggen wetenschappers
- Onderzoekers ontwikkelen kwantummembranen - een nieuwe klasse van 2D-halfgeleiders

- Schakelbare DNA-minimachines slaan informatie op
 Een nieuwe methode om therapieën precies in het lichaam af te leveren
Een nieuwe methode om therapieën precies in het lichaam af te leveren Een kwestie van vertrouwen:moeten bazen werknemers kunnen bespioneren, ook als ze thuis werken?
Een kwestie van vertrouwen:moeten bazen werknemers kunnen bespioneren, ook als ze thuis werken? Tienden van een pond omrekenen naar Ounces
Tienden van een pond omrekenen naar Ounces Houd je vrienden dichtbij
Houd je vrienden dichtbij Colloïdale quantum dot fotodetectoren kunnen nu verder kijken dan voorheen
Colloïdale quantum dot fotodetectoren kunnen nu verder kijken dan voorheen Een gemengd getal converteren naar een breuknotatie
Een gemengd getal converteren naar een breuknotatie  Hoe een percentage in uren te converteren
Hoe een percentage in uren te converteren  Fun Archimedes Principe Experimenten
Fun Archimedes Principe Experimenten
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

