
Wetenschap
Een bal mag op hetzelfde moment van de bovenkant van de toren 200 m hoog vallen, een andere verticaal verticaal opwaartse bodem met een snelheid 40 meter per seconde?
Inzicht in het probleem
* bal 1: Versnomen uit rust (beginsnelheid =0 m/s) vanaf een hoogte van 200 m.
* bal 2: Omhoog gegooid met een beginsnelheid van 40 m/s vanaf de grond (hoogte =0 m).
veronderstellingen
* We negeren de luchtweerstand voor eenvoud.
* We gebruiken standaardversnelling vanwege de zwaartekracht (g =9,8 m/s²)
Berekeningen
bal 1 (vallen van de toren)
* Vergelijking: We kunnen de bewegingsvergelijking gebruiken:
* h =ut + (1/2) gt²
* waar:
* h =hoogte (200 m)
* U =Initiële snelheid (0 m/s)
* g =versnelling als gevolg van zwaartekracht (9,8 m/s²)
* t =tijd
* Oplossen voor tijd (t):
* 200 =0t + (1/2) (9.8) t²
* 200 =4.9t²
* t² =40.82
* T ≈ 6.39 seconden (dit is de tijd die de bal nodig heeft om de grond te bereiken)
BALL 2 (omhoog gegooid)
* Vergelijking: We kunnen dezelfde vergelijking gebruiken, maar met een andere beginsnelheid:
* h =ut + (1/2) gt²
* het vinden van de tijd om de maximale hoogte te bereiken:
* Op de maximale hoogte is de uiteindelijke snelheid (V) 0 m/s.
* We kunnen de vergelijking gebruiken:v =u + gt
* 0 =40 + (-9.8) t (Opmerking:G is negatief omdat het naar beneden werkt)
* t ≈ 4.08 seconden (dit is de tijd die nodig is om de maximale hoogte te bereiken)
Het vinden van de hoogte van de bal 2 op het moment dat bal 1 de grond bereikt
* We weten dat Ball 1 6,39 seconden nodig heeft om de grond te bereiken.
* Laten we op dat moment de hoogte van de bal 2 vinden:
* h =40 (6.39) + (1/2) (-9.8) (6.39) ²
* H ≈ -34.42 meter (dit betekent dat bal 2 al onder de grond is)
Conclusie
De twee ballen zullen elkaar niet in de lucht ontmoeten. Bal 1 zal eerst de grond bereiken. Tegen de tijd dat Ball 1 de grond raakt, zal Ball 2 het grondniveau al hebben gepasseerd en naar beneden blijven.
 Is substantie smeltbewijs dat er een chemische verandering is opgetreden?
Is substantie smeltbewijs dat er een chemische verandering is opgetreden?  Waarom is chloor een gas bij kamertemperatuur, maar natriumchloride vaste temperatuur?
Waarom is chloor een gas bij kamertemperatuur, maar natriumchloride vaste temperatuur?  Welke maakt geen deel uit van nucleaire chemie?
Welke maakt geen deel uit van nucleaire chemie?  Het proces van zuurstof dat reageert met een metaal om roest te vormen?
Het proces van zuurstof dat reageert met een metaal om roest te vormen?  Fermentatie produceert ATP in aanwezigheid van zuurstof?
Fermentatie produceert ATP in aanwezigheid van zuurstof?
 Kettingreactie van snel drainerende meren vormt een nieuw risico voor de Groenlandse ijskap
Kettingreactie van snel drainerende meren vormt een nieuw risico voor de Groenlandse ijskap Levenscyclus van de Okapi
Levenscyclus van de Okapi  Wat is de sfeer in de kunst?
Wat is de sfeer in de kunst?  Genetica kan koraalriffen helpen beschermen tegen de opwarming van de aarde
Genetica kan koraalriffen helpen beschermen tegen de opwarming van de aarde Een win-winsituatie voor bossen en kleinschalige melkveehouderij in Oost-Afrika
Een win-winsituatie voor bossen en kleinschalige melkveehouderij in Oost-Afrika
Hoofdlijnen
- Nieuw soort cognitieve robot... een puppy?
- Hoe jonge kippen spelen, kan aangeven hoe ze zich voelen
- Hoe virussen werken
- Wat zijn de voor- en nadelen van endotherm zijn?
- Wat gebeurt er als er sprake is van mitose?
- Opwarming van het klimaat zou de bacteriële impact op Chesapeake Bay-schelpdieren kunnen vergroten, recreatie
- Is een zonnebloem prokaryotisch of eukaryotisch?
- Een gebied met een grote populatie waardevolle oceaanorganismen wordt een wat genoemd?
- Wat is een andere celnaam voor transplantaatafstotcellen?
- Supergeleidend metamateriaal vangt kwantumlicht op

- Een laserfocus op super waterafstotende metalen

- Verfrommeld Mylar bleek te onthouden hoe lang het verfrommeld was

- Het snel comprimeren van lood tot drukken van het planetaire kerntype blijkt het sterker te maken dan staal
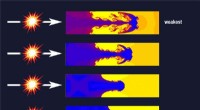
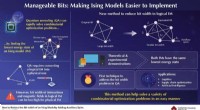
- Een beetje te veel:het verkleinen van de bitbreedte van Ising-modellen voor kwantumgloeien
 Wat veroorzaakte veel gebeurtenissen van het vulkanisme en aardbevingen van het berggebouw in het westen van Noord -Amerika tijdens het Cenozoïcum?
Wat veroorzaakte veel gebeurtenissen van het vulkanisme en aardbevingen van het berggebouw in het westen van Noord -Amerika tijdens het Cenozoïcum?  Hoe vindt u roosterconstante
Hoe vindt u roosterconstante Hoe de spanning in een touw te berekenen
Hoe de spanning in een touw te berekenen  Hoe het belastingpakket de scheiding van kerk en politiek zou kunnen vervagen
Hoe het belastingpakket de scheiding van kerk en politiek zou kunnen vervagen Wat gebeurt er met de zwaartekracht wanneer twee objecten van elkaar worden verplaatst?
Wat gebeurt er met de zwaartekracht wanneer twee objecten van elkaar worden verplaatst?  Beeldvorming van geaccumuleerde ladingen op vaste-elektrolytinterfaces
Beeldvorming van geaccumuleerde ladingen op vaste-elektrolytinterfaces Hoeveel neutronen zijn er in een atoom van molybdeen MO-96?
Hoeveel neutronen zijn er in een atoom van molybdeen MO-96?  Wat zijn de drie categorieën sedimentaire rotsen?
Wat zijn de drie categorieën sedimentaire rotsen?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

