
Wetenschap
Een bal wordt gedropt van een hoogte van 100 cm bij elke bounce, hij heft de helft van de verhoogde met eerdere vindafstand af die bedekt zijn tot tot rust komt?
Inzicht in het patroon
* Eerste drop: 100 cm
* Eerste stuitering: 100 cm / 2 =50 cm (omhoog) + 50 cm (omlaag) =100 cm
* Tweede stuitering: 50 cm / 2 =25 cm (omhoog) + 25 cm (omlaag) =50 cm
* Derde bounce: 25 cm / 2 =12,5 cm (omhoog) + 12,5 cm (omlaag) =25 cm
En zo op ...
het berekenen van de totale afstand
Dit vormt een geometrische serie waar:
* De eerste term (a) is 100 cm
* De gemeenschappelijke verhouding (R) is 1/2
De totale afstand is de som van de oneindige geometrische serie:
S =A / (1 - R)
S =100 cm / (1 - 1/2)
S =100 cm / (1/2)
S =200 cm
Daarom zal de bal een totale afstand van 200 cm afleggen voordat hij tot rust komt.
 Om enquêtes en ander onderzoek te verbeteren, bestuderen entomologen hoe kleuren wilde bijen aantrekken
Om enquêtes en ander onderzoek te verbeteren, bestuderen entomologen hoe kleuren wilde bijen aantrekken  Onderzoek plaatst natuurbrandrisico in historische context
Onderzoek plaatst natuurbrandrisico in historische context Afbeelding:Petermann-gletsjer, Groenland
Afbeelding:Petermann-gletsjer, Groenland Deze gemeenschappen experimenteren met groenere en eerlijkere manieren van leven
Deze gemeenschappen experimenteren met groenere en eerlijkere manieren van leven Broeikasgasemissies van internationale scheepvaart nemen toe
Broeikasgasemissies van internationale scheepvaart nemen toe
Hoofdlijnen
- Naast eiwitten wordt organische moleculen ook gevonden in cellulaire membranen?
- Wetenschappers ontdekken pad naar verbeterde gerstkwaliteit
- Wat is de functie van ribosomen in plantencel?
- Waarom gebeurt convergente evolutie?
- Onderzoek zou de weg kunnen vrijmaken voor een beter begrip van de manier waarop planten en dieren groeien en zich ontwikkelen
- Het type organismen dat voedselergie door een gemeenschap overdragen en uiteindelijk eten met andere zijn de?
- Wat is het tweede niveau van organisatie in een meercellulair organisme?
- Waarom en hoe voert u een strengtest?
- Wetenschappelijke tijdschriften tonen weinig handhaving van de rapportagerichtlijnen voor dieronderzoek
- Verrassende communicatie tussen atomen kan kwantumcomputers verbeteren

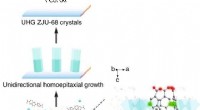
- Metal Organic Framework (MOF) microkristallen voor meerkleurige breedbandlasing
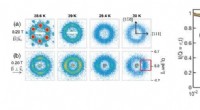
- De invloed van een magnetisch veld op chirale magnetische correlaties
- 10 prestatieverhogende medicijnen die geen steroïden zijn

- Eerste massameting met zeldzame-RI-ring onthult fijne structuur van patronen van overvloed aan elementen

 De oneindig kleine pakt namaak aan
De oneindig kleine pakt namaak aan Welke dieren eten planten en dieren?
Welke dieren eten planten en dieren?
Een dier dat zowel planten als andere dieren eet, is geclassificeerd als een alleseter. Er zijn twee soorten alleseters; diegenen die op jacht prooien: zoals herbivoren en andere omnivoren, en degenen die speure
 Hoe heet een holle gletsjer?
Hoe heet een holle gletsjer?  AT&T's Time Warner-overname heeft de mediawereld al hervormd
AT&T's Time Warner-overname heeft de mediawereld al hervormd Wat voor soort fysieke hoeveelheid is 12,1 meter per seconde?
Wat voor soort fysieke hoeveelheid is 12,1 meter per seconde?  Welke drie elementen komen voor in organische moleculen?
Welke drie elementen komen voor in organische moleculen?  Eerste blik op waterstof op het grensvlak van metaal-op-metaalhydride
Eerste blik op waterstof op het grensvlak van metaal-op-metaalhydride Wat gebeurt er als je een gezin met een laag inkomen $ 26.000 geeft in het eerste jaar van hun kind? We denken dat we erachter zijn gekomen
Wat gebeurt er als je een gezin met een laag inkomen $ 26.000 geeft in het eerste jaar van hun kind? We denken dat we erachter zijn gekomen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

