
Wetenschap
Welke snelheid heeft de space shuttle om aan de zwaartekracht van de aarde te ontsnappen?
Om de snelheid te berekenen die de space shuttle nodig heeft om aan de zwaartekracht van de aarde te ontsnappen, kunnen we de volgende formule gebruiken:
$$v_e =\sqrt{2GM_E/R_E}$$
Waar:
v_e is de ontsnappingssnelheid
G is de zwaartekrachtconstante (G ≈ 6,67430 x 10^-11 N·m²/kg²)
M_E is de massa van de aarde (M_E ≈ 5,972 x 10^24 kg)
R_E is de straal van de aarde (R_E ≈ 6,378 x 10^6 m)
Waarden invoeren:
$$v_e =\sqrt{(2 x 6,67430 x 10^-11 N·m²/kg² x 5,972 x 10^24 kg)/(6,378 x 10^6 m)}$$
Als we het resultaat berekenen, krijgen we:
$$v_e ≈ 11.180 m/s$$
De space shuttle moet dus een snelheid bereiken van ongeveer 11.180 meter per seconde (ongeveer 25.000 mijl per uur) om aan de zwaartekracht van de aarde te ontsnappen en de ruimte in te gaan.
Hoofdlijnen
- Slapen alle dieren?
- Celwand: definitie, structuur en functie (met diagram)
- Een DNA-model maken met behulp van pijpreinigers
- Waar bevinden lipiden zich in het lichaam?
- Hoe lijken mitochondriën en chloroplasten op bacteriën?
- Hoe je hersenen werken
- Geërgerd door andere volkeren friemelen? Studie zegt dat je niet alleen bent
- Kunnen dieren iriserende kleuren gebruiken om te communiceren?
- Verschil tussen plantaardige en dierlijke celdeling
- Natuurkundigen stellen nieuw model voor om koppelingseigenschappen van kernen te bestuderen

- Waarom produceert kernsplijting peervormige kernen?

- Wetenschappers stellen nieuwe bron voor zeldzame subatomaire deeltjes voor
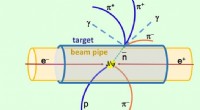
- Quarks waargenomen interactie via minuscule zwakke lichtzwaarden
- Elektronen die op een laserstraal surfen

 Wat gebeurt er met een metaal dat wordt blootgesteld aan zure mengsels?
Wat gebeurt er met een metaal dat wordt blootgesteld aan zure mengsels?  Vodafone krijgt 200 miljoen euro treffer van Huawei 5G stoepranden
Vodafone krijgt 200 miljoen euro treffer van Huawei 5G stoepranden De stralingsshowstopper voor Mars-exploratie
De stralingsshowstopper voor Mars-exploratie Astronauten hebben een verrassend vermogen om te weten hoe ver ze in de ruimte 'vliegen'
Astronauten hebben een verrassend vermogen om te weten hoe ver ze in de ruimte 'vliegen'  Stermedewerkers krijgen de meeste eer en de schuld
Stermedewerkers krijgen de meeste eer en de schuld Wat veroorzaakt de meeste verwering op het aardoppervlak?
Wat veroorzaakt de meeste verwering op het aardoppervlak?  Hoe face-to-face Facebook nog steeds verslaat:Beperkingen op de omvang van onze offline sociale groepen gelden ook online
Hoe face-to-face Facebook nog steeds verslaat:Beperkingen op de omvang van onze offline sociale groepen gelden ook online  Autobranche projecten met eigen aandrijving
Autobranche projecten met eigen aandrijving
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com


