
Wetenschap
Een ruimtestation heeft de vorm van een ring en draait om de zwaartekracht te simuleren. Als de straal van 110 m met welke frequentie moet het draaien zodat de zwaartekracht wordt gesimuleerd?
Om de zwaartekracht te simuleren moet het ruimtestation roteren met een frequentie die een centripetale versnelling creëert die gelijk is aan de versnelling als gevolg van de zwaartekracht op aarde, namelijk ongeveer 9,8 m/s². De centripetale versnelling wordt gegeven door de vergelijking:
$$a_c =\frac{v^2}{r}$$
waar:
- \(a_c\) is de centripetale versnelling
- \(v\) is de tangentiële snelheid
- \(r\) is de rotatiestraal
Door de centripetale versnelling gelijk te stellen aan 9,8 m/s² en de tangentiële snelheid op te lossen, krijgen we:
$$v =\sqrt{a_c \cdot r} =\sqrt{9,8 \text{ m/s}^2 \cdot 110 \text{ m}} =33,20 \text{ m/s}$$
De rotatiefrequentie wordt dan gegeven door:
$$f =\frac{v}{2\pi r} =\frac{33,20 \text{ m/s}}{2\pi \cdot 110 \text{ m}} =0,1514 \text{ Hz}$$
Daarom moet het ruimtestation roteren met een frequentie van ongeveer 0,1514 Hz om de zwaartekracht te simuleren.
 Elektronenkristallografie bleek net zo goed te werken als röntgenkristallografie alleen op kleinere kristallen
Elektronenkristallografie bleek net zo goed te werken als röntgenkristallografie alleen op kleinere kristallen Wat is de chemische verbinding voor argon?
Wat is de chemische verbinding voor argon?  Het combineren van atomistische simulaties en machinaal leren om de segregatie van korrelgrenzen in magnesiumlegeringen te voorspellen
Het combineren van atomistische simulaties en machinaal leren om de segregatie van korrelgrenzen in magnesiumlegeringen te voorspellen  Helder en efficiënt licht zonder zeldzame metalen
Helder en efficiënt licht zonder zeldzame metalen Zuurstofproductie afschermen om waterstof aan te houden
Zuurstofproductie afschermen om waterstof aan te houden
 De rol van klimaatverandering in elke storm aanwijzen is onmogelijk, en een luxe die de meeste landen zich niet kunnen veroorloven
De rol van klimaatverandering in elke storm aanwijzen is onmogelijk, en een luxe die de meeste landen zich niet kunnen veroorloven Japanse vulkaan barst uit, tientallen vluchten aan de grond
Japanse vulkaan barst uit, tientallen vluchten aan de grond Een surrealistisch beeld van Australië door kunstenaars - gemaakt op basis van satellietgegevens die 700 km boven de aarde zijn vastgelegd
Een surrealistisch beeld van Australië door kunstenaars - gemaakt op basis van satellietgegevens die 700 km boven de aarde zijn vastgelegd De ontwikkeling van een diepzee-broeikasgasfilter observeren
De ontwikkeling van een diepzee-broeikasgasfilter observeren Wie zal de rechter zijn over de klimaatplannen van landen?
Wie zal de rechter zijn over de klimaatplannen van landen?
Hoofdlijnen
- Onderzoek toont aan dat commerciële oogst van brekende schildpadden leidt tot bevolkingsafname
- Hoe duurzaam is tonijn? Nieuwe mondiale vangstdatabank legt gevaarlijke visserijtrends bloot
- Het sociale leven van weesolifanten is aanzienlijk veranderd door stroperij
- Onderzoeker onthult hoe kevers terugveren van bosbranden
- Malawi wendt zich tot Britse troepen in stropersoorlog
- Zijn mannen gewelddadiger dan vrouwen?
- Bronnen van de Lactase Enzyme
- Hoe kan DNA worden gebruikt om de theorie te ondersteunen dat alle soorten een gemeenschappelijke afkomst delen?
- Uit onderzoek blijkt dat eiwitten een sleutelrol spelen bij het helpen van cilium om signalen naar de rest van de cel over te brengen
- Gebruik maken van geluid voor de gezondheid

- Communicatieapparaat biedt enorm bandbreedtepotentieel

- Visualisatie van mechanische golven in een vloeibaar medium

- Een nieuwe niet-invasieve techniek voor de diagnose van perkament
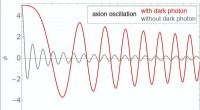
- Onderzoek naar het samenspel tussen axionen en donkere fotonen in het vroege heelal
 Belangrijkste onderdeel om quantum computing op te schalen
Belangrijkste onderdeel om quantum computing op te schalen SpaceX introduceert nieuwe bemanningscapsule tijdens cruciale testvlucht
SpaceX introduceert nieuwe bemanningscapsule tijdens cruciale testvlucht Onderzoekers gebruiken door laser gegenereerde bubbels om 3D-afbeeldingen in vloeistof te maken
Onderzoekers gebruiken door laser gegenereerde bubbels om 3D-afbeeldingen in vloeistof te maken De neiging van de allelen op één chromosoom om samen te erven, wordt genoemd?
De neiging van de allelen op één chromosoom om samen te erven, wordt genoemd?  Je kunt SpaceX-speelgoed en verzamelobjecten kopen vanaf volgend jaar
Je kunt SpaceX-speelgoed en verzamelobjecten kopen vanaf volgend jaar De Medicago-genoomsequentie werpt nieuw licht op hoe planten stikstofbindende symbiose ontwikkelden
De Medicago-genoomsequentie werpt nieuw licht op hoe planten stikstofbindende symbiose ontwikkelden  Mangroven in Florida onthullen complexe relatie tussen klimaat en natuurlijke systemen
Mangroven in Florida onthullen complexe relatie tussen klimaat en natuurlijke systemen Studie onderzoekt hoe songwriters uit Nashville samen met sterren schrijven
Studie onderzoekt hoe songwriters uit Nashville samen met sterren schrijven
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

