
Wetenschap
Hoe snel beweegt lucht met een snelheidsdruk van 0,20 in w.g. door vierkante buis bewegen?
De snelheidsdruk wordt gedefinieerd als:
$$P_v=\frac{1}{2}\rho V^2$$
waar:
- \(P_v\) is de snelheidsdruk in Pa
- \(\rho\) is de dichtheid van de lucht in kg/m³
- \(V\) is de snelheid van de lucht in m/s
We kunnen deze vergelijking herschikken om de snelheid op te lossen:
$$V=\sqrt{\frac{2P_v}{\rho}}$$
Als we de gegeven waarden vervangen, krijgen we:
$$V=\sqrt{\frac{2(0,20\text{ in wg})(47,88\text{ Pa/in wg})}{1,225\text{ kg/m}^3}}$$
$$V=5,67\text{ m/s}$$
Daarom is de lucht met een snelheidsdruk van 0,20 in w.g. beweegt door het vierkante kanaal met een snelheid van 5,67 m/s.
 Nieuwe manier van testen op cocaïne ontdekt
Nieuwe manier van testen op cocaïne ontdekt Wat is propyleenglycol
Wat is propyleenglycol Halogeenbinding-gemedieerde metaalvrije gecontroleerde kationische polymerisatie
Halogeenbinding-gemedieerde metaalvrije gecontroleerde kationische polymerisatie Hoe het zeeleven reageert op verzuring van de oceaan
Hoe het zeeleven reageert op verzuring van de oceaan  Opgewonden multimeer gemedieerde supramoleculaire opconversie op lanthanide-organische assemblages met meerdere componenten
Opgewonden multimeer gemedieerde supramoleculaire opconversie op lanthanide-organische assemblages met meerdere componenten
Hoofdlijnen
- Auto-immuniteit kan verklaren waarom een belangrijk immuunsysteem bij veel bacteriën ontbreekt
- Onderzoekers beschrijven hoe cellen het afval buiten zetten om ziekten te voorkomen
- Waarom blozen mensen?
- Mendels Experimenten: The Study of Pea Plants & Inheritance
- Voorbeelden van archaebacteriën met hun wetenschappelijke naam en classificatie
- Wetenschappers zouden supermodelbouwers moeten zijn
- Stijgende zeetemperaturen bedreigen Atlantische populaties van Bulwers-stormvogels
- Wat is een voorbeeld van een kanaaleiwit?
- Robotapparaat volgt plantengroei op cellulair niveau
- Ingenieurs ontwikkelen nieuwe methode voor het oplossen van spintextuur van topologische oppervlaktetoestanden met behulp van transportmetingen
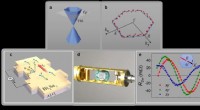
- Onderzoekers voltooien de eerste fase van het experiment om gigantische luchtdouches te bestuderen

- Een lasersysteem gebouwd op principes van supersymmetrie

- Hafnia krijgt een nieuw gezicht:materiaalonderzoek creëert potentieel voor verbeterde computerchips en transistors

- Een beter begrip krijgen van wat er gebeurt als twee atomen elkaar ontmoeten

 Ruimtesonde duikt in vurige corona van de zon
Ruimtesonde duikt in vurige corona van de zon Hoe magneten aantrekken & afstoten?
Hoe magneten aantrekken & afstoten?  Revolutionair ontwerp en analyse van supergeleidende magneetplaten
Revolutionair ontwerp en analyse van supergeleidende magneetplaten Californië tot zweepslag tussen droogte, overstromingen:studie
Californië tot zweepslag tussen droogte, overstromingen:studie Bio-ingenieurs zetten stap in de richting van een patch die een gebroken hart kan herstellen
Bio-ingenieurs zetten stap in de richting van een patch die een gebroken hart kan herstellen Mentale rigiditeit aan de basis van intense politieke partijdigheid zowel links als rechts
Mentale rigiditeit aan de basis van intense politieke partijdigheid zowel links als rechts Waarom Amerikanen het nooit eens zullen worden over olieboringen in het Arctic National Wildlife Refuge
Waarom Amerikanen het nooit eens zullen worden over olieboringen in het Arctic National Wildlife Refuge Er zijn aanwijzingen dat veel tornado's groter en sterker zijn dan gerapporteerd
Er zijn aanwijzingen dat veel tornado's groter en sterker zijn dan gerapporteerd
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

