
Wetenschap
Wetenschappers onderzoeken informatievoortplanting in op elkaar inwerkende bosonische systemen
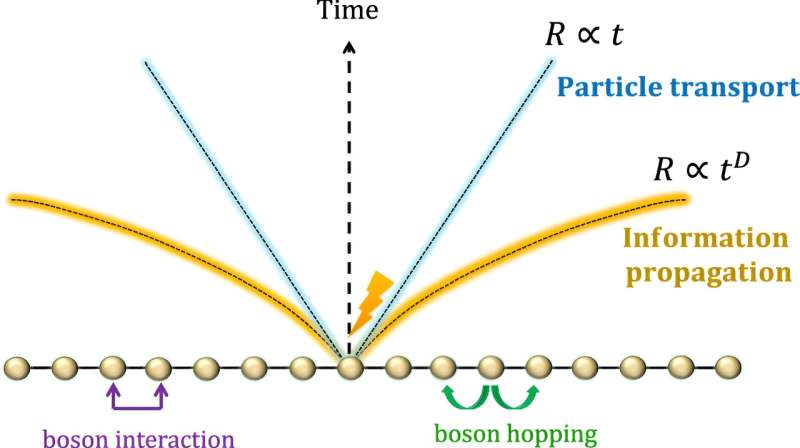
Een nieuwe studie door wetenschappers uit Japan onderzoekt de verspreiding van kwantuminformatie binnen op elkaar inwerkende bosonsystemen zoals Bose-Einstein-condensaten (BEC's), waardoor het potentieel voor versnelde transmissie wordt onthuld, anders dan eerder werd gedacht.
Kwantumveeldeeltjessystemen zijn, net als op elkaar inwerkende bosonsystemen, van fundamenteel belang omdat ze toepassingen vinden in verschillende takken van de natuurkunde. De voortplanting van informatie in kwantumsystemen met veel lichamen wordt beheerst door de Lieb-Robinson-grens. Dit kwantificeert hoe snel informatie of veranderingen zich door een kwantumsysteem voortplanten.
Wanneer u een wijziging aanbrengt in een deel van het systeem, beschrijft de Lieb-Robinson-grens de snelheid waarmee deze verandering andere delen van het systeem beïnvloedt. In praktische termen betekent dit dat het effect van uw initiële verandering zich vanaf het beginpunt naar buiten zal verspreiden en aangrenzende regio's van het systeem zal beïnvloeden.
De Lieb-Robinson die op weg is naar interagerende bosonsystemen is echter lange tijd een uitdaging gebleven.
De onderzoekers, onder leiding van Dr. Tomotaka Kuwahara, de RIKEN Hakubi-teamleider bij het RIKEN Center for Quantum Computing, gaan deze uitdaging aan in hun nieuwe Nature Communications studeren.
Dr. Kuwahara legde het belang van hun werk uit aan Phys.org en benadrukte het belang van het begrijpen van kwantumsystemen die fundamentele deeltjes zoals bosonen en fermionen bevatten.
"De bosonsystemen hebben in principe geen energielimiet, wat de Lieb-Robinson-binding in bosonische systemen aanzienlijk uitdagend maakte", zei hij.
De Lieb-Robinson-grens
Zoals eerder vermeld, biedt de Lieb-Robinson-grens een kwantitatieve limiet voor hoe snel correlaties of invloeden zich kunnen verspreiden tussen ruimtelijk gescheiden gebieden van een kwantumsysteem.
Wat dit betekent is dat de voortplanting niet overal onmiddellijk kan plaatsvinden en in plaats daarvan beperkt is tot een effectieve lichtkegel. Geïnspireerd door de relativiteitstheorie van Einstein vertegenwoordigt de lichtkegel alle punten in ruimte en tijd die een lichtsignaal van een gebeurtenis kan bereiken. Hierdoor ontstaat een dubbele kegel:één voor het verleden en één voor de toekomst.
Hetzelfde geldt voor informatievoortplanting in kwantumsystemen met meerdere lichamen, dat wil zeggen systemen met meer dan twee kwantumdeeltjes.
"De Lieb-Robinson-grens stelt een universele snelheidslimiet in voor hoe snel informatie in deze systemen kan reizen", legt Dr. Kuwahara uit.
Volgens de Lieb-Robinson-grens is de verspreiding van informatie beperkt en vervalt deze exponentieel met de afstand of de tijd. De details van het verval zijn afhankelijk van het individuele systeem en de interacties die binnen het systeem kunnen plaatsvinden.
De Lieb-Robinson-grens, geformuleerd door Elliott Lieb en Derek Robinson in 1972, is alleen van toepassing op niet-relativistische systemen, dat wil zeggen dat de informatie zich verplaatst met snelheden die veel lager zijn dan de snelheid van het licht.
Het Bose-Hubbard-model
Op elkaar inwerkende bosonsystemen bestaan uit vele bosonen (zoals fotonen). Hoewel deze systemen vaak voorkomen, brengen ze veel uitdagingen met zich mee, zoals langeafstandsinteracties tussen bosonen en onbegrensde energie, waardoor het moeilijk wordt om simulaties en theoretische modellen te ontwikkelen.
Maar sinds de ontdekking van de BEC zijn modellen zoals het Bose-Hubbard-model ontwikkeld om bosonische systemen te bestuderen. Het Bose-Hubbard-model is een theoretisch raamwerk dat wordt gebruikt om te begrijpen hoe bosonen zich gedragen wanneer ze beperkt zijn tot een roosterstructuur, zoals atomen in een kristal.
Dit model houdt rekening met twee belangrijke factoren. De eerste is het springen van bosonen van de ene roosterplaats naar de andere, weergegeven door de hopping-parameter. Ten tweede is er de interactieparameter ter plaatse, die de afstotende krachten tussen bosonen vertegenwoordigt wanneer ze dezelfde locatie bezetten. Deze interactie-energie neemt toe naarmate meer bosonen dezelfde locatie bezetten.
Deze factoren omvatten de interactie tussen de bosonen. Daarom kozen de onderzoekers voor het Bose-Hubbard-model om de Lieb-Robinson-grenzen in op elkaar inwerkende bosonsystemen te onderzoeken.
De bovengrenzen
De onderzoekers kozen ervoor om de Lieb-Robinson te bestuderen op weg naar een D-dimensionaal rooster (interacterend bosonsysteem) dat wordt bestuurd door het Bose-Hubbard-model. Ze hebben drie resultaten gevonden voor dit systeem.
Resultaat 1
Dit resultaat richt zich op de interactie van bosonen binnen het rooster. De onderzoekers ontdekten dat de snelheid van bosontransport beperkt is, zelfs in systemen met langeafstandsinteracties. Deze snelheid, hoewel beperkt, groeit hoogstens logaritmisch met de tijd, wat relatief langzaam is.
Deze bevinding biedt cruciale inzichten in de dynamiek van bosonsystemen, waardoor een bovengrens wordt gesteld aan de snelheid ervan.
Resultaat 2
Dit resultaat richt zich op de verspreiding van operators van het systeem in de loop van de tijd. Operators zijn in principe variabelen van het systeem, zoals momentum. Terwijl deze operatoren zich voortplanten, wijken ze af van de ideale evolutie, wat leidt tot een opeenstapeling van fouten.
Deze foutvoortplanting bepaalt hoe snel informatie zich in het systeem kan voortplanten. Als de fout bijvoorbeeld groot is, geeft dit aan dat de informatievoortplanting langzamer of beperkter is, omdat de benadering aanzienlijk afwijkt van de ideale evolutie van het systeem.
Op dezelfde manier, als de fout klein is, is de informatievoortplanting snel. Dit komt overeen met de Lieb-Robinson-grens, wat de aanwezigheid van een bovengrens voor de voortplanting van fouten aangeeft.
Ondanks de aanwezigheid van een bovengrens voor de voortplanting van fouten, veroorzaken interacties tussen bosonen clustering in specifieke regio's. Deze regio's, gekenmerkt door hogere bosonconcentraties, faciliteren versnelde informatievoortplanting langs bepaalde roosterpaden of -richtingen.
Dit fenomeen komt overeen met de Lieb-Robinson-grens. Deze versnelling is echter begrensd en kent een polynomiale groei, afhankelijk van de dimensionaliteit van het systeem.
Resultaat 3
Dit resultaat biedt een manier om deze systemen te simuleren met behulp van elementaire kwantumpoorten (zoals CNOT). De onderzoekers geven een bovengrens voor het aantal elementaire kwantumpoorten dat nodig is voor het efficiënt simuleren van de tijdsevolutie van op elkaar inwerkende bosonsystemen.
Vergelijking met fermionische systemen
Fermionische systemen laten een eindige snelheidslimiet zien voor hoe snel informatie zich kan voortplanten. Vóór dit werk gingen wetenschappers ervan uit dat hetzelfde geldt voor bosonische systemen, wat niet waar is.
‘De lichtkegel verspreidt zich veel sneller en is niet-lineair, dat wil zeggen:hij versnelt in de loop van de tijd. Als je specifiek naar een driedimensionale ruimte kijkt, groeit de afstand die ‘informatie’ kan afleggen met het kwadraat van de tijd. In die zin kunnen bosonen dus veel sneller informatie verzenden dan fermionen, vooral naarmate de tijd verstrijkt", legt dr. Kuwahara uit.
Dit hangt af van het aantal bosonen dat tegelijkertijd dezelfde toestand kan innemen. In wezen geldt dat hoe meer bosonen meedoen, hoe sneller informatie zich kan verspreiden.
‘Maar omdat bosonen slechts met een eindige snelheid kunnen bewegen, kost het wat tijd voordat veel bosonen bij elkaar komen, wat leidt tot een beperkte snelheid van informatievoortplanting. Naarmate meer bosonen samenwerken, neemt de snelheid waarmee ze samenwerken toe. kan informatie verzenden gaat omhoog," zei Dr. Kuwahara.
Dit werk opent een nieuw venster in het verkennen van op elkaar inwerkende bosonsystemen voor informatievoortplanting.
"Ik verwacht dat het algoritme zal worden gebruikt om de fysica van de gecondenseerde materie te simuleren, wat zou kunnen leiden tot de ontdekking van nieuwe kwantumfasen. Het zou ook nuttig moeten blijken bij het simuleren van kwantumthermisatie, waardoor de fundamentele vraag kan worden beantwoord hoe gesloten kwantumsystemen zich in een systeem nestelen." stabiele toestand in de loop van de tijd”, concludeerde Dr. Kuwahara.