
Wetenschap
De fysica van een zingende zaag

De onderzoekers klemden de zaag in twee configuraties vast:een J-vorm (links) en een S-vorm (rechts). De S-vorm heeft een buigpunt (de sweet spot) in zijn profiel, terwijl de J-vorm dat niet heeft. Tegoed: Mahadevan Lab/Harvard SEAS
Het griezelige, etherische geluid van de zingende zaag is een onderdeel van volksmuziektradities over de hele wereld, van China tot de Appalachen, sinds de verspreiding van goedkoop, flexibel staal in het begin van de 19e eeuw. Gemaakt door een metalen handzaag te buigen en te buigen als een cello, bereikte het instrument zijn hoogtijdagen op de vaudeville-podia van het begin van de 20e eeuw en heeft het een opleving gezien, mede dankzij sociale media.
Het blijkt dat de unieke wiskundige fysica van de zingende zaag de sleutel kan zijn tot het ontwerpen van hoogwaardige resonatoren voor een reeks toepassingen.
In een nieuw artikel gebruikte een team van onderzoekers van de Harvard John A. Paulson School of Engineering and Applied Sciences (SEAS) en het Department of Physics de zingende zaag om aan te tonen hoe de geometrie van een gebogen plaat, zoals gebogen metaal, kan worden afgestemd om hoogwaardige, langdurige oscillaties te creëren voor toepassingen in detectie, nano-elektronica, fotonica en meer.
"Ons onderzoek biedt een robuust principe om hoogwaardige resonatoren te ontwerpen, onafhankelijk van schaal en materiaal, van macroscopische muziekinstrumenten tot apparaten op nanoschaal, simpelweg door een combinatie van geometrie en topologie", zegt L Mahadevan, de Lola England de Valpine Professor of Applied Mathematics. , van Organismic and Evolutionary Biology, en van Physics en senior auteur van de studie.
Het onderzoek is gepubliceerd in The Proceedings of the National Academy of Sciences (PNAS ).
Hoewel alle muziekinstrumenten een soort akoestische resonator zijn, werkt geen enkele zo als de zingende zaag.
"Hoe de zingende zaag zingt, is gebaseerd op een verrassend effect", zegt Petur Bryde, een afgestudeerde student aan SEAS en mede-eerste auteur van het artikel. "Als je een platte elastische plaat raakt, zoals een plaat metaal, trilt de hele structuur. De energie gaat snel verloren door de grens waar deze wordt vastgehouden, wat resulteert in een dof geluid dat snel verdwijnt. Hetzelfde resultaat wordt waargenomen als je buig het in een J-vorm. Maar als je het blad in een S-vorm buigt, kun je het in een heel klein gebied laten trillen, wat een heldere, langdurige toon oplevert."
De geometrie van de gebogen zaag creëert wat muzikanten de 'sweet spot' noemen en wat natuurkundigen gelokaliseerde trillingsmodi noemen:een beperkt gebied op het blad dat resoneert zonder energie te verliezen aan de randen.
Belangrijk is dat de specifieke geometrie van de S-curve er niet toe doet. Het kan een S zijn met een grote curve aan de bovenkant en een kleine curve aan de onderkant of omgekeerd.
"Muzikanten en onderzoekers weten al geruime tijd van dit robuuste effect van geometrie, maar de onderliggende mechanismen zijn een mysterie gebleven", zegt Suraj Shankar, een Harvard Junior Fellow in Physics and SEAS en mede-eerste auteur van het onderzoek. "We hebben een wiskundig argument gevonden dat verklaart hoe en waarom dit robuuste effect bestaat bij elke vorm binnen deze klasse, zodat de details van de vorm onbelangrijk zijn, en het enige dat er toe doet, is dat er een omkering van de kromming langs de zaag is. "
Shankar, Bryde en Mahadevan vonden die verklaring via een analogie met een heel andere klasse van fysieke systemen:topologische isolatoren. Meestal geassocieerd met kwantumfysica, zijn topologische isolatoren materialen die elektriciteit geleiden in hun oppervlak of rand, maar niet in het midden, en het maakt niet uit hoe je deze materialen snijdt, ze zullen altijd aan hun randen geleiden.
"In dit werk hebben we een wiskundige analogie getrokken tussen de akoestiek van gebogen platen en deze kwantum- en elektronische systemen", zegt Shankar.
Door de wiskunde van topologische systemen te gebruiken, ontdekten de onderzoekers dat de gelokaliseerde trillingsmodi in de goede plek van zingende zaag werden bepaald door een topologische parameter die kan worden berekend en die op niets meer berust dan het bestaan van twee tegengestelde krommen in het materiaal. De sweet spot gedraagt zich dan als een interne "rand" in de zaag.
"Door experimenten, theoretische en numerieke analyse te gebruiken, hebben we aangetoond dat de S-kromming in een dunne schaal topologisch beschermde modi kan lokaliseren op de 'sweet spot' of buiglijn, vergelijkbaar met exotische randtoestanden in topologische isolatoren," zei Bryde. "Dit fenomeen is materiaalonafhankelijk, wat betekent dat het zal verschijnen in staal, glas of zelfs grafeen."
De onderzoekers ontdekten ook dat ze de lokalisatie van de modus konden afstemmen door de vorm van de S-curve te veranderen, wat belangrijk is in toepassingen zoals detectie, waarbij je een resonator nodig hebt die is afgestemd op zeer specifieke frequenties.
Vervolgens willen de onderzoekers gelokaliseerde modi verkennen in dubbel gebogen structuren, zoals bellen en andere vormen. + Verder verkennen
Wiskundig raamwerk verandert elk vel materiaal in elke vorm met behulp van kirigami-sneden
 Het vermogen van SIRT6 om de groei van kankercellen te onderdrukken wordt uitgelegd
Het vermogen van SIRT6 om de groei van kankercellen te onderdrukken wordt uitgelegd Herziening van de rol van planten in antibacteriële activiteit maakt nieuwe paden vrij voor het ontdekken van geneesmiddelen
Herziening van de rol van planten in antibacteriële activiteit maakt nieuwe paden vrij voor het ontdekken van geneesmiddelen Slimme diëlektrische elastomeren voor zelfherstellende zachte robots
Slimme diëlektrische elastomeren voor zelfherstellende zachte robots supercomputeren, neutronen verenigen zich om structuren van intrinsiek ongeordend eiwit te ontrafelen
supercomputeren, neutronen verenigen zich om structuren van intrinsiek ongeordend eiwit te ontrafelen Mysterie van faseverandering in sub-nanoseconde-octaëders structuurmotief
Mysterie van faseverandering in sub-nanoseconde-octaëders structuurmotief
 De zomer van klimaatextremen dit jaar treft rijkere plaatsen
De zomer van klimaatextremen dit jaar treft rijkere plaatsen Google gebruiken om ons ecosysteem in kaart te brengen
Google gebruiken om ons ecosysteem in kaart te brengen Veel aanrijdingen tussen dieren en voertuigen te voorkomen
Veel aanrijdingen tussen dieren en voertuigen te voorkomen Nieuw VN-rapport onthult onthutsende menselijke klimaatvoetafdruk op water en ijs
Nieuw VN-rapport onthult onthutsende menselijke klimaatvoetafdruk op water en ijs Enorme behoefte aan groeiende bomen op boerderijen
Enorme behoefte aan groeiende bomen op boerderijen
Hoofdlijnen
- Grazende paarden op betere weiden
- Ingenieurs hacken celbiologie om 3D-vormen te maken van levend weefsel
- Lood visgerei kan een bedreiging vormen voor de populaties van duikers
- Wetenschappers roepen de VS op om onderzoek naar potmedicijnen voor huisdieren toe te staan
- Eksters kunnen vriendschappen sluiten met mensen - dit is hoe
- Herdersactiviteiten overdag hebben geen negatieve invloed op gevlekte hyena's in Tanzania
- Door het uitbreiden van het DNA-alfabet kunnen cellen nieuwe eiwitten produceren
- Top 5 manieren om plezier te hebben in 2050
- Nadat de dinosauriërs waren verdwenen, werden zoogdieren sneller groter en stierven ze jong
- Wetenschappers ontwerpen nieuwe MRI-spoel voor preklinische studies

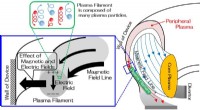
- Een miljard plasmadeeltjes berekenen in een supercomputer
- Innovatieve benadering voor het beheersen van magnetisme opent de weg naar microchips met ultralaag vermogen

- Langlevend pionisch helium:exotische materie voor het eerst experimenteel geverifieerd

- Hogesnelheidscamera legt een spetterende impact van waterstralen vast terwijl deze een druppel doorboort

 Krachtige trivalente remmers van trombine uit antistollingspeptiden in speeksel van insecten
Krachtige trivalente remmers van trombine uit antistollingspeptiden in speeksel van insecten Sleutel tot het vinden van een baan na de universiteit? Stages, in het buitenland studeren, undergraduate onderzoek en meer
Sleutel tot het vinden van een baan na de universiteit? Stages, in het buitenland studeren, undergraduate onderzoek en meer Een nieuwe methode om afbeeldingen van oude munten te begrijpen
Een nieuwe methode om afbeeldingen van oude munten te begrijpen Nanobuiscomposieten verhogen de efficiëntie van de volgende generatie zonnecellen
Nanobuiscomposieten verhogen de efficiëntie van de volgende generatie zonnecellen De strijd voor schone uitstoot gaat door
De strijd voor schone uitstoot gaat door Video:Larsen-C ijsplaat barst
Video:Larsen-C ijsplaat barst Milieu beleid, vervuiling en economische groei
Milieu beleid, vervuiling en economische groei NASA kijkt naar Kalmaegis-waterdampconcentratie bij tropische depressie
NASA kijkt naar Kalmaegis-waterdampconcentratie bij tropische depressie
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

