
Wetenschap
De vorming van gap solitons in een 1D dissipatief topologisch rooster
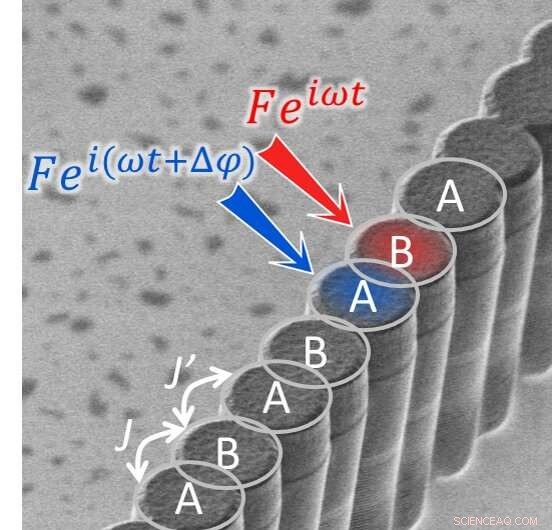
Scanning-elektronenmicroscopiebeeld dat een ketting van halfgeleiderholten toont. De afstand tussen de holtes wordt gemoduleerd, wat aanleiding geeft tot twee verschillende waarden van de koppeling J en J' tussen aangrenzende holtes (schematisch weergegeven door dubbele witte pijlen). Deze modulatie van de koppeling geeft het rooster topologische eigenschappen. Twee holtes van het rooster worden geëxciteerd door twee lasers met amplitude F, hoekfrequentie en presenteren een faseverschil. Krediet:C2N/CNRS.
Topologische fotonica is een snel evoluerend onderzoeksgebied dat zich richt op het ontwerp van fotonische roosters waarbij het gedrag van licht is geïnspireerd op de fysica van topologische isolatoren. Terwijl de meeste studies op dit gebied fotonische systemen met lineaire topologische eigenschappen presenteerden, zijn recente werken begonnen met het leggen van de fundamenten van niet-lineaire topologische fotonica.
Onderzoekers van de Université Paris-Saclay CNRS hebben onlangs de niet-lineaire respons gerapporteerd van een topologisch rooster dat een gedreven-dissipatieve versie van het Su-Schrieffer-Heeger-model implementeert; een gerenommeerd elementair topologisch raamwerk dat deeltjes die op een 1D-rooster springen beschrijft. De bevindingen verzameld door het team van Université Paris-Saclay CNRS, gepubliceerd in Nature Physics , laten zien dat coherent rijden in topologische roosters kan worden benut, waardoor natuurkundigen nieuwe niet-lineaire fasen kunnen stabiliseren.
"In 2017 demonstreerde onze groep de eerste topologische laser met behulp van een 1D-raster van halfgeleiderresonator dat erg lijkt op het rooster dat in onze recente studie werd gebruikt," vertelde Sylvain Ravets en Jacqueline Bloch, twee van de onderzoekers die het onderzoek uitvoerden, aan Phys.org . "In dit vroege werk gebruikten we echter de lineaire topologische eigenschappen van het systeem."
De recente studie van Ravets, Bloch en hun collega's bouwt voort op hun eerdere onderzoeksinspanningen, met als doel hun onderzoek uit te breiden tot niet-lineaire topologische fysica, die tot nu toe voornamelijk is onderzocht in de context van conservatieve systemen. In hun experimenten gebruikten de onderzoekers een platform met een significante optische niet-lineariteit, die onderhevig is aan continue drive en dissipatie.
"We gebruikten nanotechnologieën om een 1D-raster van gekoppelde niet-lineaire resonatoren te fabriceren," legden Ravets en Bloch uit. "Elke resonator bestaat uit een optische holte die een actief medium bevat (een halfgeleider-kwantumbron), die voor de niet-lineariteit zorgt. De koppeling tussen aangrenzende holtes is verspringend om het eenvoudigste topologische model te implementeren, bekend als het Su Schrieffer Heger-model. "
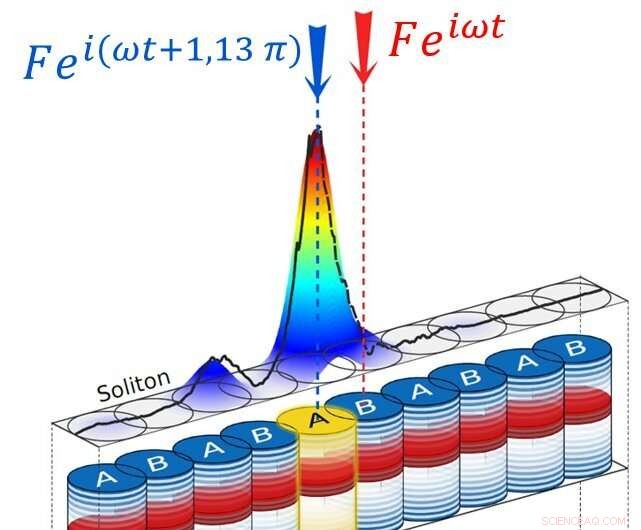
Illustratie van de nieuwe familie van dissipatieve gap solitons ontdekt door de onderzoekers voor het gemeten intensiteitsprofiel van een dergelijke soliton wordt bovenaan de figuur getoond. De intensiteit is zeer sterk op één enkele site, wat leidt tot de spectrale ontstemming van deze site ten opzichte van de rest van de keten. De ketting wordt dus effectief verbroken en er verschijnt een randtoestand in het excitatiespectrum, zoals weergegeven onderaan de figuur. Krediet:C2N/CNRS.
Om een niet-lineaire respons in hun 1D-rooster te veroorzaken, schenen Ravets, Bloch en hun collega's een of twee laserstralen op specifieke delen van het rooster. Vervolgens controleerden ze de uitgezonden intensiteit als functie van het ingevoerde laservermogen.
"Een bijzonder relevante knop die we in ons experiment hebben gebruikt, is de relatieve fase tussen de excitatiestralen, wat een nieuw controleniveau biedt waar tot nu toe niet aan was gedacht", aldus Ravets en Bloch.
De experimenten van de onderzoekers leverden nieuwe en interessante resultaten op. In het bijzonder ontdekte het team de vorming van nieuwe gap soliton-families, die worden gestabiliseerd door de resonante excitatie. Deze gap solitons bestaan niet in conservatieve systemen, zoals gekoppelde golfgeleiders die werken in propagatieve geometrieën.
"Deze solitonen hebben hetzelfde profiel als een topologische randtoestand en veroorzaken in feite het verschijnen van een topologische randtoestand voor excitaties bovenop de niet-lineaire stabiele toestand. We noemen dit vermogen om het systeem te besturen door de engineering van de laserexcitatie schema 'drive engineering'", aldus Ravets en Bloch.
De recente studie van Ravets, Bloch en hun collega's benadrukt de mogelijkheid om coherent rijden te benutten om niet-lineaire fasen in topologische fotonische systemen te stabiliseren. In de toekomst kunnen de experimentele methoden die in hun paper worden beschreven, worden gebruikt om de topologie van 1D-fotonische systemen te controleren en kunnen ze ook worden uitgebreid naar 2D-systemen.
"In onze volgende studie zijn we van plan deze ideeën uit te breiden naar fotonische topologische isolatoren in 2D-roosters, waarbij ons doel zal zijn om het vermogen aan te tonen om de topologie van een niet-lineair fotonisch rooster optisch te regelen door middel van de engineering van de aandrijving en dissipatie." Ravets en Bloch toegevoegd. + Verder verkennen
De experimentele demonstratie van topologische dissipatie in fotonische resonatoren
© 2022 Science X Network
 Leven met luchtvervuiling
Leven met luchtvervuiling Het noordpoolgebied is in 3 miljoen jaar niet zo warm geweest – en dat voorspelt grote veranderingen voor de rest van de planeet
Het noordpoolgebied is in 3 miljoen jaar niet zo warm geweest – en dat voorspelt grote veranderingen voor de rest van de planeet Afrikaanse landen houden zich aan 1,5C-doelstelling bij klimaatgesprekken
Afrikaanse landen houden zich aan 1,5C-doelstelling bij klimaatgesprekken Wolkencamera Gemini Observatory legt dramatische gloed van vulkanen vast
Wolkencamera Gemini Observatory legt dramatische gloed van vulkanen vast Isaias slaat Amerikaanse oostkust met felle wind, zware regen
Isaias slaat Amerikaanse oostkust met felle wind, zware regen
Hoofdlijnen
- Wetenschappers volgen aseksuele kleine wormen - waarvan de afstamming 18 miljoen jaar teruggaat
- De mens als model voor het begrijpen van biologische fundamenten
- Vijf redenen om de insecten in je tuin niet te besproeien
- Verrassing in de kangoeroe-stamboom - een buitenstaander is een naast familielid, ten slotte
- Dino-dodende asteroïde versnelde evolutie van vogels
- Wereldwijd onderzoeksteam vult taalkloof in plantenwetenschap
- Soorten zenuwen in het menselijk lichaam
- Oude voetafdrukken op Brits strand record ondergang van hotspot voor biodiversiteit
- Panspermia:zorgden buitenaardse zaden ervoor dat het leven op aarde explodeerde?
- Het vloeistofvolume berekenen

- Onderzoekers ontsluiten geheimen voor de zwemefficiëntie van walvissen, dolfijnen voor next-gen onderwaterrobots

- Chickensplash! Onderzoek naar de gezondheidsproblemen van het wassen van rauwe kip
- T-ray-technologie onthult wat er onder je huid gebeurt

- Onderzoekers maken een biosensor door spinnenzijde om te zetten in optische vezels

 Nieuwe, goedkope aanpak detecteert vervormingen van gebouwen met extreme precisie in realtime
Nieuwe, goedkope aanpak detecteert vervormingen van gebouwen met extreme precisie in realtime Klimaatverandering en smeltende gletsjers hebben zeer uiteenlopende gevolgen voor de Aziatische watervoorziening
Klimaatverandering en smeltende gletsjers hebben zeer uiteenlopende gevolgen voor de Aziatische watervoorziening Hoe massa te vinden van dichtheid
Hoe massa te vinden van dichtheid  Top 5 programma's die nieuwe toepassingen vinden voor oude technologieën
Top 5 programma's die nieuwe toepassingen vinden voor oude technologieën  Onderzoekers kunnen rekenen op verbeterde proteomics-methode
Onderzoekers kunnen rekenen op verbeterde proteomics-methode Franse hotelgigant AccorHotels koopt het Zwitserse Movenpick
Franse hotelgigant AccorHotels koopt het Zwitserse Movenpick Voedselverspilling:steden kunnen het verschil maken
Voedselverspilling:steden kunnen het verschil maken Kleine tools:individuele waterdruppels besturen als biochemische reactoren
Kleine tools:individuele waterdruppels besturen als biochemische reactoren
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

