
Wetenschap
De thermodynamica van het leven krijgt vorm
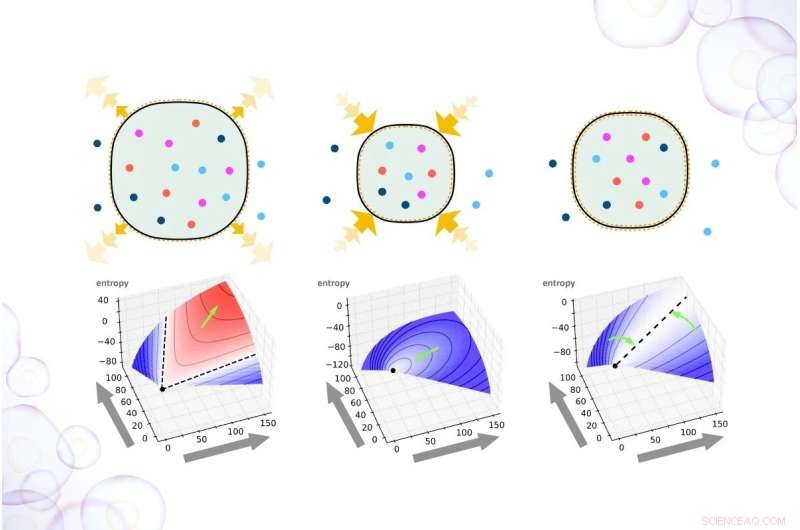
Credit:Instituut voor Industriële Wetenschappen, Universiteit van Tokyo (UTokyo-IIS)
Het onthullen van de wetenschappelijke wetten die onze wereld beheersen, wordt door wetenschappers vaak als de "heilige graal" beschouwd, aangezien dergelijke ontdekkingen verstrekkende implicaties hebben. In een opwindende ontwikkeling uit Japan hebben wetenschappers laten zien hoe ze geometrische representaties kunnen gebruiken om de wetten van de thermodynamica te coderen, en deze representaties toe te passen om algemene voorspellingen te verkrijgen. Dit werk kan ons begrip van de theoretische limieten die gelden binnen de chemie en biologie aanzienlijk verbeteren.
Hoewel levende systemen gebonden zijn aan de wetten van de fysica, vinden ze vaak creatieve manieren om van deze regels te profiteren op manieren die niet-levende fysieke systemen zelden kunnen. Elk levend organisme vindt bijvoorbeeld een manier om zichzelf te reproduceren. Op een fundamenteel niveau is dit afhankelijk van autokatalytische cycli waarin een bepaald molecuul de productie van identieke moleculen kan stimuleren, of een reeks moleculen elkaar produceren. Als onderdeel hiervan groeit het compartiment waarin de moleculen zich bevinden in volume. Het ontbreekt echter aan wetenschappelijke kennis aan een volledige thermodynamische representatie van dergelijke zelfreplicerende processen, die wetenschappers in staat zouden stellen te begrijpen hoe levende systemen kunnen ontstaan uit niet-levende objecten.
Nu, in twee gerelateerde artikelen gepubliceerd in Physical Review Research , gebruikten onderzoekers van het Instituut voor Industriële Wetenschappen van de Universiteit van Tokyo een geometrische techniek om de omstandigheden te karakteriseren die overeenkomen met de groei van een zelfreproducerend systeem. Het leidende principe is de beroemde tweede wet van de thermodynamica, die vereist dat entropie - in het algemeen opgevat als wanorde - alleen maar kan toenemen. Een toename van de volgorde is echter mogelijk, zoals een bacterie die voedingsstoffen opneemt om zich in twee bacteriën te kunnen delen, maar ten koste van een verhoogde entropie ergens anders. "Zelfreplicatie is een kenmerk van levende systemen, en onze theorie helpt de omgevingsomstandigheden te verklaren om hun lot te bepalen, of het nu gaat om groei, krimp of evenwicht", zegt senior auteur Tetsuya J. Kobayashi.
Het belangrijkste inzicht was om de thermodynamische relaties weer te geven als hyperoppervlakken in een multidimensionale ruimte. Vervolgens zouden de onderzoekers kunnen bestuderen wat er gebeurt als verschillende operaties worden uitgevoerd, in dit geval met behulp van de Legendre-transformatie. Deze transformatie beschrijft hoe een oppervlak in kaart kan worden gebracht in een ander geometrisch object met een significante thermodynamische betekenis.
"De resultaten zijn uitsluitend verkregen op basis van de tweede wet van de thermodynamica dat de totale entropie moet toenemen. Hierdoor waren aannames van een ideaal gas of andere vereenvoudigingen over de soorten interacties in het systeem niet vereist", zegt eerste auteur Yuki Sughiyama. Het kunnen berekenen van de snelheid van entropieproductie kan van vitaal belang zijn voor het evalueren van biofysische systemen. Dit onderzoek kan helpen de studie van de thermodynamica van levende systemen op een meer solide theoretische basis te brengen, wat ons begrip van biologische reproductie kan verbeteren.
De artikelen zijn gepubliceerd in Physical Review Research als "Hessische geometrische structuur van chemische thermodynamische systemen met stoichiometrische beperkingen" en "Chemische thermodynamica voor groeiende systemen." + Verder verkennen
Veroudering, entropie en verspilling:beschadigde cellen wegspoelen
 Video:Geeft adrenaline je superheldenkracht?
Video:Geeft adrenaline je superheldenkracht? AI zocht naar single-atom-alloy katalysatoren, 200 veelbelovende kandidaten gevonden
AI zocht naar single-atom-alloy katalysatoren, 200 veelbelovende kandidaten gevonden Een nieuwe klasse membranen belooft interessante toepassingen in materiaalscheiding
Een nieuwe klasse membranen belooft interessante toepassingen in materiaalscheiding Bereken de gemiddelde temperatuur
Bereken de gemiddelde temperatuur  Dynamische afbeeldingen tonen ruitvormige protease in actie
Dynamische afbeeldingen tonen ruitvormige protease in actie
Hoofdlijnen
- Nieuwe online database brengt het genoom in beeld met behulp van moleculaire structuur
- Waarom hebben zoveel van onze huisdieren overgewicht?
- DNA-tests op albatrospoep onthullen geheim dieet van toproofdier
- Turkije bevrijdt 7, 500 illegaal opgejaagde kikkers de rivier in
- Wat is een geest? Onderzoeker daagt percepties van gevoel uit met de kleinste wezens
- Klimaatverandering kan leiden tot intensere sprinkhanenuitbraken en een bedreiging vormen voor de voedselzekerheid
- Hoe de cellen van planten, dieren en eencellige organismen te vergelijken
- 3D-analyse van hondenfossielen werpt licht op het debat over domesticatie
- 7 soorten bindweefsel
- Onderzoekers observeren lasergestuurde tin-ejecta-microjet-interacties

- Weer een stukje in de donkere materie puzzel plaatsen

- Een stap dichter bij de toekomst van kwantumcomputers

- Bruinvissen bleken voorhoofdweefsel te verschuiven om sonarsignalen te verfijnen

- Supermans laservisie een stap dichter bij de realiteit

 PNNL-technologie maakt de weg vrij voor van ethanol afgeleide vliegtuigbrandstof
PNNL-technologie maakt de weg vrij voor van ethanol afgeleide vliegtuigbrandstof Berekeningsmethoden voor vijfde graad wiskunde
Berekeningsmethoden voor vijfde graad wiskunde  Frankrijk blokkeert ontwikkeling van Facebook Libra-cryptocurrency
Frankrijk blokkeert ontwikkeling van Facebook Libra-cryptocurrency E-textiel krijgt een mode-upgrade met geheugenopslagvezel
E-textiel krijgt een mode-upgrade met geheugenopslagvezel NASA-regenbeelden laten zien dat Norbert de status van tropische storm terugkrijgt
NASA-regenbeelden laten zien dat Norbert de status van tropische storm terugkrijgt Een waterafstotend nanomateriaal geïnspireerd door de natuur
Een waterafstotend nanomateriaal geïnspireerd door de natuur Waarschuwing tegen klimaatverandering van ingestorte oude steden
Waarschuwing tegen klimaatverandering van ingestorte oude steden De voordelen van MOSFET boven BJT
De voordelen van MOSFET boven BJT
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

